专栏文章

题解：P6579 [Ynoi2019] Happy Sugar Life

EEterna
P6579题解参与者 1已保存评论 0

文章操作

快速查看文章及其快照的属性，并进行相关操作。

当前评论
0 条
当前快照
1 份
快照标识符
@min1c5d7
此快照首次捕获于
2025/12/01 18:57
3 个月前
此快照最后确认于
2025/12/01 18:57
3 个月前
查看原文
区间查询某值域内的顺序对数。
对于所有点 (i,ai)(i,a_i) 建立平面直角坐标系如下：
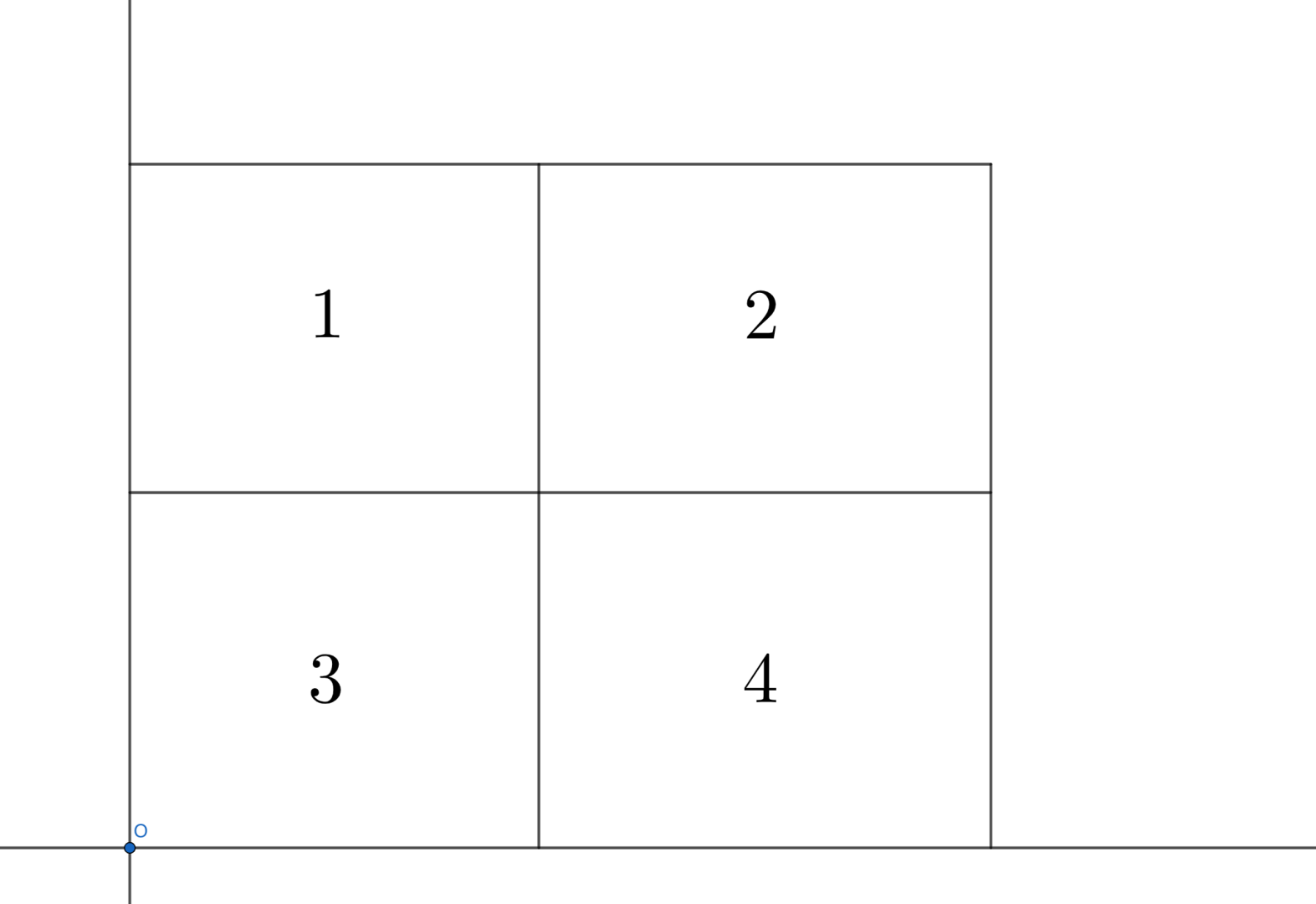
现在我们要计算部分 (1,2,3,4)(1,2,3,4) 的答案 s1,2,3,4s_{1,2,3,4}。
可以变为 s1,2,3,4=s1,2+s3,4+s1,3+s2,4+s1,4+s2,3−s1−s2−s3−s4s_{1,2,3,4}=s_{1,2}+s_{3,4}+s_{1,3}+s_{2,4}+s_{1,4}+s_{2,3}-s_{1}-s_{2}-s_{3}-s_{4}。
对于更多行列的情况，答案为每行答案加每列答案加行列均不同的两部分构成的答案减去每个部分的答案。
考虑树套树的结构，则一次询问在序列和值域上均被划分为 O(log⁡n)\mathcal{O}(\log n) 层。
  1. 对于每行答案或每列答案显然可以用相同的方法求出，以每列答案为例：
    可以对于每列将询问挂在行上，每次列上的询问相当于区间顺序对。
    这样，对于行上的树结构，每一层都有 O(m)\mathcal{O}(m) 个询问。
    考虑使用莫队二次离线解决。则复杂度为 T(n)=2T(n/2)+O(nm)=O(nm)T(n)=2T(n/2)+\mathcal{O}(n\sqrt{m})=\mathcal{O}(n\sqrt{m})。
  2. 对于行列均不同的答案。显然，若这个行列均不同的两部分顺序是对的，将两部分点的数量相乘即可。
  3. 对于每个部分的答案。考虑使用线段树合并计算，然后每组询问可以直接 O(log⁡2n)\mathcal{O}(\log^2 n) 枚举。
于是我们在 O(nm+mlog⁡2n)\mathcal{O}(n\sqrt{m}+m \log ^2 n) 的时间复杂度内解决这个问题。
tips：对于莫队二次离线，我们将其中扫描线的复杂度略去。因为扫描线部分可以 o(nn)o(n\sqrt{n})。且 O(nn)\mathcal{O}(n\sqrt{n}) 在这题本身就小于 O(nm)\mathcal{O}(n\sqrt{m})。

评论

共 0 条评论，欢迎与作者交流。

正在加载评论...