题解：CF2163C Monopati

官解怎么在双指针，不会啊呜呜。

首先一个很自然的想法是，因为 down-right path 只有

n

种，那么直接枚举这

n

条路线，不妨设第

i

条路线为

(1,1)\to(1,i)\to(2,i)\to(2,n)

，路线上的点的点权的最大值为

y_i

，最小值为

x_i

，则符合题意的数对集合为

\{(l,r)|1\leqslant l\leqslant x_i,y_i\leqslant r\leqslant 2n\}

，显然对于第

i

条路线数对个数为

x_i(2n+1-y_i)

。

实现部分，设

pre_{1,i,0/1}

存储第一行每个前缀的最小值/最大值，

suf_{2,i,0/1}

存储第二行每个后缀的最小值/最大值，那么可以直接求出

x_i=\min(pre_{1,i,0},suf_{2,i,0}),y_i=\max(pre_{1,i,1},suf_{2,i,1})

，是很简单的前/后缀和应用。

但是你很快会发现，一个

(l,r)

数对可能可以走两种以上不同路线，但是计数时只能被计入一次，怎么办呢？难道容斥吗？

n\leqslant 2\cdot10^5

，肯定不能直接容斥。重新审视我们需要求的柿子：

\left|\bigcup\limits_{i=1}^n\{(l,r)|1\leqslant l\leqslant x_i,y_i\leqslant r\leqslant 2n\}\right|

，我们注意到每一个集合在二维平面上都是一个矩形的形式！啊？矩形面积并？div2C 出线段树加扫描线？真的假的？

其实不需要。发现实际上矩形的左边界和上边界实际上是固定的，我们只需要记录右下角

(x_i,y_i)

的露尖（代表这个矩形），如果出现了一个矩形

(x^\prime,y^\prime)

被另一个矩形

(x,y)

全包含的情况（即

x^\prime\leqslant x,y^\prime\geqslant y

），那么直接忽略掉

(x^\prime,y^\prime)

即可。于是剩下来的矩形（设有

m

个）按照右下尖的横坐标排序，右下尖的纵坐标就是递增的，每个矩形的实际贡献就是这个矩形减去下一个矩形即

\{(l,r)|1\leqslant l\leqslant x_i,y_i\leqslant r< y_{i+1}\}

（不妨

y_{m+1}=2n+1

），即最终答案为

\sum\limits_{i=1}^mx_i(y_{i+1}-y_i)

。

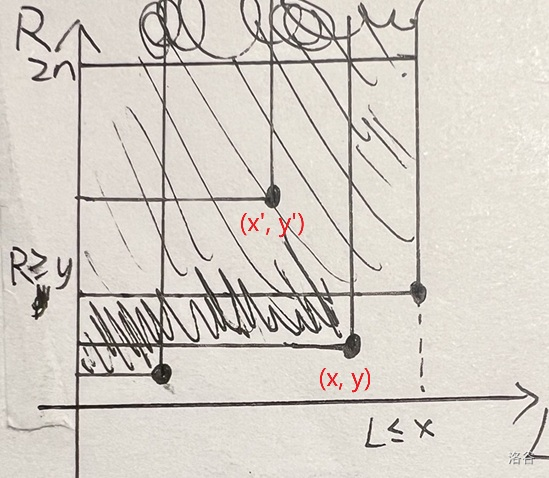
不是我想要的矩形，直接去掉。去掉被包含矩形的实现与去掉被包含区间（去掉子集和去掉超集都考的很多，甚至下一题就又考一遍）类似，可以直接用单调栈维护，先对横坐标排序，栈顶元素小于等于当前元素就一直弹出栈顶，然后当前元素入栈。具体实现可以参考 AC Code。

CPP

#include<bits/stdc++.h>
#define rep(i,x,y) for(int i = (x); i <= (y); i++)
#define x first
#define y second
typedef long long ll;
typedef std::pair<int, int> pii;
ll read() {ll x; scanf("%lld", &x); return x;}
using std::min, std::max;
const int N = 214514;
int n, a[2][N];
pii pre[N], suf[N], p[N];
int main() {
    int T = read(); while(T--) {
        n = read();
        rep(i, 0, 1) rep(j, 1, n) a[i][j] = read();
        pre[1] = {a[0][1], a[0][1]};
        rep(i, 2, n) {
            pre[i].x = min(a[0][i], pre[i - 1].x);
            pre[i].y = max(a[0][i], pre[i - 1].y);
        }
        suf[n] = {a[1][n], a[1][n]};
        for(int i = n - 1; i; i--) {
            suf[i].x = min(a[1][i], suf[i + 1].x);
            suf[i].y = max(a[1][i], suf[i + 1].y);
        }
        rep(i, 1, n) {
            p[i].x = min(suf[i].x, pre[i].x),
            p[i].y = max(suf[i].y, pre[i].y);
        }
        std::sort(p + 1, p + n + 1);
        ll ans = 0;
        std::stack<pii> st;
        rep(i, 1, n) {
            while(!st.empty() && st.top().y >= p[i].y) st.pop();
            st.push(p[i]);
        }
        int r = 2 * n + 1;
        while(!st.empty()) {
            auto [x, y] = st.top(); st.pop();
            ans += x * /**/1ll * (r - y);
            r = y;
        }
        printf("%lld\n", ans);
    }
}

题解：CF2163C Monopati

文章操作

相关推荐

评论

题解：CF2163C Monopati