专栏文章

小可爱zzz绷不住逐步绷一眼秒的题 题解

NNobleNumbat
P13948题解参与者 4已保存评论 4

文章操作

快速查看文章及其快照的属性，并进行相关操作。

当前评论
4 条
当前快照
1 份
快照标识符
@minurwp8
此快照首次捕获于
2025/12/02 08:41
3 个月前
此快照最后确认于
2025/12/02 08:41
3 个月前
查看原文

前言

小可爱zzz一眼秒了，但是我不会做。
做法来源，我的语文成绩不怎么样，所以感觉那篇题解的说明有些难以断句。我在这里再总结一下做法。

做法

由于原图是平面图，很难不想到先建出对偶图。
这里我们从图的每个顶点引出一条射线，将无限面划分成 nn 小块，这样保证了对偶图是一棵树。
考虑题目所求，两点间的最大流即为 两点之间两段弧所对应的 两组代表无限面的点的 最短路。
找一些性质。
考虑对偶图上 所有连接无限面和有限面的边中 边权最小的边，记这条边是 ee。
这类边一定能找到 唯一 包含它的 边数最小的 一个环（这里指原图上的环），记其为 CC。
那么有结论：所有最短路要么与 CC 没有交，要么与 CC 有交 而且经过 ee。
可以感性理解一下。假设 s,ts,t 引出的射线将图分成了上下两部分，而 ee 在上部分，如图。
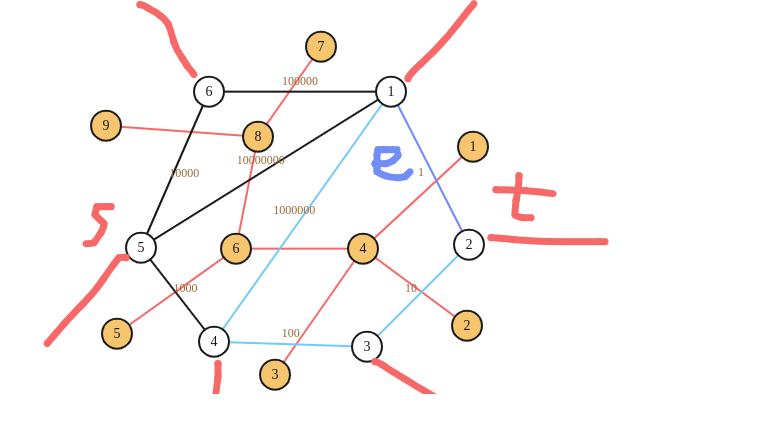
那么若最短路经过 CC 且不经过 ee，我们把 从 CC 连向上半部分无限面的路径 替换成 ee 即可。因为 ee 是边权最小的连向无限面的边，所以一定不劣。
同时，由于边权非负，那么一个面一定不会被经过两次。这个结论就证完了。
考虑从原图上删除 ee，并将 CC 上其他边边权加上 ee 的权值，形成一张新的图。
这里 在原图上删掉一条边 相当于 合并对偶图一条边连接的两个节点。
这里容易发现：
  • 原图一条满足上述结论的路径 一定对应 新图上一条路径，且长度相等。这就说明了原图最短路大于等于新图最短路。
  • 新图上一条路径的长度 一定大于等于 原图上对应路径的长度。这就说明了新图最短路大于等于原图最短路。
也就是说原图和新图上任一个点对，其最短路不变。那么我们直接删去这条边即可。这时 CC 上的其他边就可能成为新的 ee，继续删除最短的 ee，直到图变为一棵树。此时点对间路径固定，使用 kruskal 重构树计算答案即可。
贴一下代码（应该可读）：
CPP
ai3 ed[400040];
vpi t[400040];
int deg[400040];
bool flg[400040],rm[400040];
pii pt[400040];
int cn[400040];
int n,m,c;

void ade(int u,int v,int w){t[u].eb(v,w),t[v].eb(u,w),pt[w]=mkp(u,v);}

void solve(int _Tid) {
    cin>>n>>m;
    for(int i=1,u,v,w;i<=m;i++)cin>>u>>v>>w,u>v&&(swap(u,v),0),ed[i]={u,v,w};
    // 建对偶图
    sort(ed+1,ed+m+1,[&](const ai3&a,const ai3&b){return a[1]^b[1]?a[1]<b[1]:a[0]>b[0];});
    vpi st;
    for(int i=1;i<=m;i++){
        ++c;
        while(st.size()&&ed[st.back().fi][0]>=ed[i][0])ade(st.back().se,c,st.back().fi),st.pop_back();
        st.eb(i,c);
    }
    ++c,ade(st.back().se,c,st.back().fi);
    for(int i=1;i<=c;i++)deg[i]=t[i].size();
    priority_queue<pii>pq;
    for(int i=1;i<=m;i++)if(ed[i][0]==ed[i][1]-1||ed[i][0]==1&&ed[i][1]==n)pq.emplace(-ed[i][2],i),cn[i]=1,flg[deg[pt[i].fi]==1?pt[i].fi:pt[i].se]=1;else cn[i]=2;
    // 不断删除一侧为无限面的边
    while(pq.size()){
        auto[w,id]=pq.top();
        pq.pop();
        if(!cn[id])continue;
        int u=flg[pt[id].fi]?pt[id].se:pt[id].fi;
        flg[u]=1,w=-w,rm[id]=1;
        for(auto[v,id]:t[u])ed[id][2]+=w,(--cn[id])&&(pq.emplace(-ed[id][2],id),0);
    }
    vector<ai3>vec;
    // 重构树计算答案
    for(int i=1;i<=m;i++)if(!rm[i])vec.pb({ed[i][2],ed[i][0],ed[i][1]});
    sort(all(vec),greater<>());
    DSU d(n+1,-1);
    ll res=0;
    for(auto[w,u,v]:vec)if(d.getfa(u)!=d.getfa(v))res+=(ll)d[d.getfa(u)]*d[d.getfa(v)]%mod*w%mod,d.merge(u,v);
    cout<<res%mod<<'\n';
}

评论

共 4 条评论，欢迎与作者交流。

正在加载评论...