引入

给定一个排列，每次可以交换两个数，问最少交换几次可以将序列排序。由于每个数唯一出现一次，所以序列本质上是一个排列。

题解

建立有向边

i \to a[i]

，每个大小为

x

的环对答案贡献

x - 1

。

编新题

我：如果题目改为「只能交换非相邻的两个元素」，应该怎么做？

出题方法

从简单题出发，尝试 改变限制 或 调整代价定义，即可得到新题。

例1 序列排序

洛谷

切入思路

首先对

a

进行 离散化，得到

p_i = \text{离散化后 } a_i \text{ 的排名}.

记忆提示

p 可理解为 permutation（排列）、position（位置）、pointer（指针）或 parent（父节点）。

然后建图：对每个

i

建边

i \to p[i]

，应该得到一个基环森林，但仔细思考，其实是一堆环。

吃泡泡 / 吐泡泡（外援机制）

不属于环的点也能与环内的节点交换，可以看作一种「外援」。

计算每个环的代价时，需要考虑两种策略：

cost1：只在环内完成排序；
cost2：借助全局最小值进行中转（邀请外援）。

设：

$T$ 为环中元素个数；
minCircle 为环内最小值；
minAll 为全局最小值；
sum 为环内所有元素之和。

CPP

for 每个环
  cost1 = sum + minCircle * (T - 2);
  cost2 = sum + minCircle + minAll * (T + 1);
  ans += min(cost1, cost2);

思考要点：把问题简化。先分析最小的二元环，再推广到一般情况。

一维数组建图

常见的命名：

CPP

p[], nxt[], fa[];

这些数组都可以「建图」。

问题

能建图的数组通常有什么特性？

答案

数组中的每个元素表示一个编号（即一个指向关系）。

例如，

\text{nxt}[i]

表示「下一个编号」。这类结构还可以倍增。

尝试构造一个

\text{nxt}

$\text{nxt}[i]$ 表示下一个比 $a_i$ 大的编号；
$\text{nxt}[i]$ 表示下一个与 $a_i$ 不同的编号；
$\text{nxt}[i]$ 表示下一个与 $a_i$ 相同的编号。

补充例题：
P2661 信息传递

边界字符串

定义：如果字符串

b

同时是

a

的前缀和后缀，则称

b

为

a

的边界（border）。

边界的边界仍是边界。

「马甲」类比

若一个人有多个身份（前缀=后缀），就像穿了多层马甲。

前缀最大边界

定义

\pi_i

表示前缀

s[1..i]

的最大边界长度。
举例一个字符串 xyzhxyzhhxyzhxyzh

i	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
$s_i$	x	y	x	h	x	y	x	h	h	x	y	x	h	x	y	x
$\pi_i$	0	0	1	0	1	2	3	4	0	1	2	3	4	5	6	7

\pi_i \in [0, i)

。

这就是 KMP算法（Knuth–Morris–Pratt）中的 fail 或 nxt 数组。

KMP算法实现

CPP

int nxt[MAXN];
char s[MAXN];
cin >> (s + 1);
int n = strlen(s + 1);

int j = 0;
nxt[1] = 0;
for (int i = 2; i <= n; i++) {
  while (j && s[i] != s[j + 1]) j = nxt[j];
  if (s[i] == s[j + 1]) j++;
  nxt[i] = j;
}

复杂度证明

关键在于 while (j && s[i] != s[j + 1])。因为指针 j 只会整体增减

O(n)

次，所以总复杂度为

O(n)

。

失配树（Fail Tree）

将每个位置

i

与其 fail[i] 相连，得到一棵树。它描述了前缀间的包含关系。

i	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
$s_i$	x	y	x	h	x	y	x	h	h	x	y	x	h	x	y	x
$\pi_i$	0	0	1	0	1	2	3	4	0	1	2	3	4	5	6	7

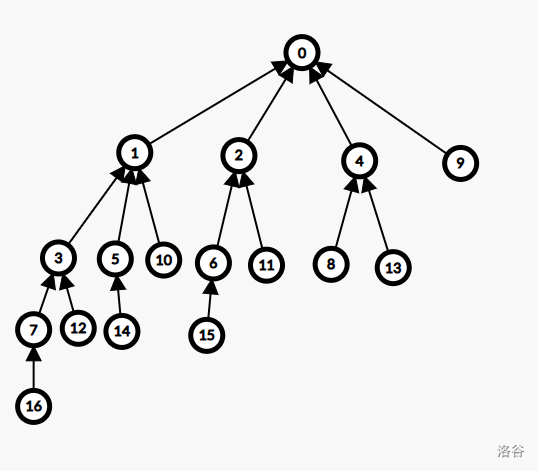
性质

$\pi_i$ 既是位置编号，也是前缀长度；
儿子节点的编号一定大于父节点；
树形结构整体向左倾斜。

猜想:儿子编号越小，对应子树越大或越高。

存在

6 \to 2

必然意味着存在

5 \to 1

。
所以这是对的

进一步观察：

$d[i]-1$ （ $d[i]$ 为深度， $d[0]=0$ ）表示前缀 $s[1..i]$ 的边界数。
$sz[i]$ （子树大小）表示前缀 $s[1..i]$ 在整个串中出现的次数。
$\mathrm{lca}(i,j)$ 表示前缀 $s[1..i]$ 与 $s[1..j]$ 的最长公共后缀。

思考：为何要建树？

补充例题：
P3375 KMP模板
P3435 OKR-Periods of Words

总结：思维转化

核心方法：

将序列或字符串转化为 区间 / 平面点 / 图论结构，从结构出发理解规律与性质。

AI使用说明

使用 ChatGPT 进行润色。

序列问题转化

文章操作

引入