专栏文章

题解：P14333 [JOI2021 预选赛 R2] 安全检查 / Safety Inspection

__Weslie_
P14333题解参与者 1已保存评论 0

文章操作

快速查看文章及其快照的属性，并进行相关操作。

当前评论
0 条
当前快照
1 份
快照标识符
@min3qndr
此快照首次捕获于
2025/12/01 20:04
3 个月前
此快照最后确认于
2025/12/01 20:04
3 个月前
查看原文
绿题？1h 才切？

Solution P14333

首先瞪一眼就知道是二分答案。然后考虑能否让所有工人在 tt 的时间内完成工作。
下面称向右移 11 位的操作为“移动”，检查是否故障的操作为“工作”。
贪心问题 11
是否会出现样例 11 解释那样，让某个工人在第一个开始修复的位置之后跳过某个位置（扔给队友完成，然后继续工作的情况？
如果你不理解我在说什么
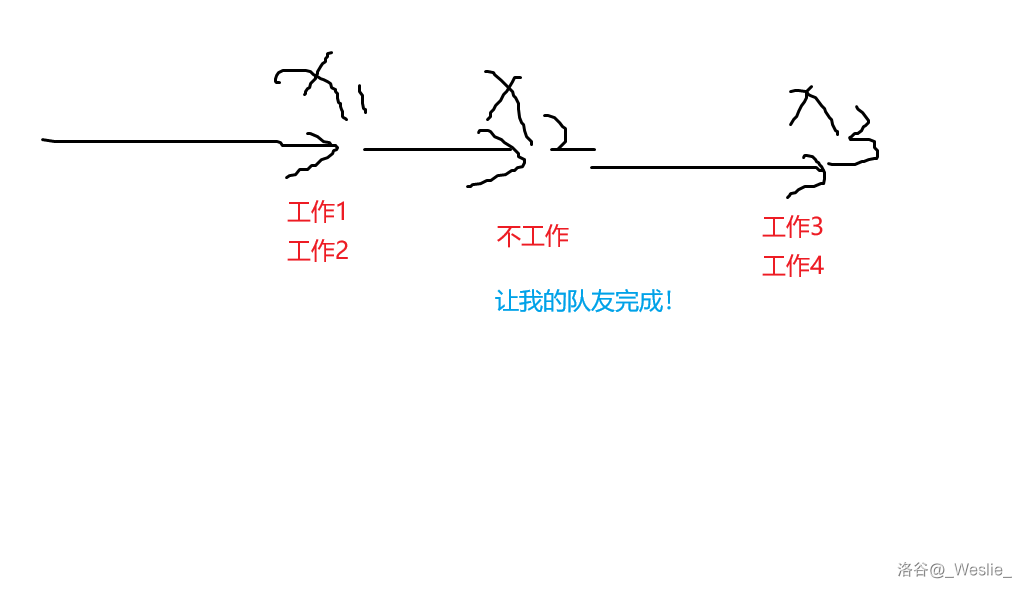
结论
不会出现。
考虑以下情况：
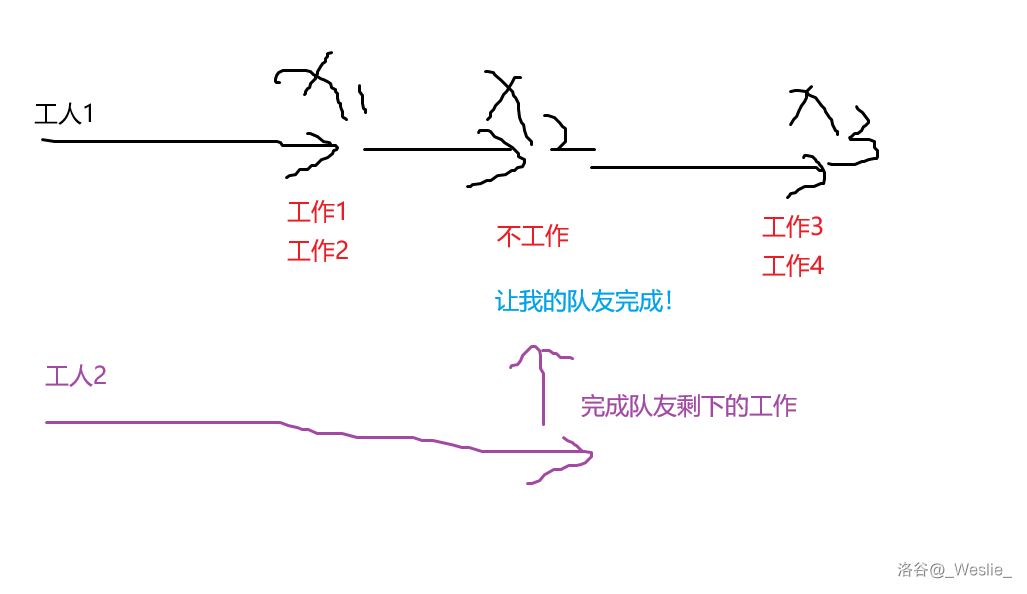
和下面的情况对比：
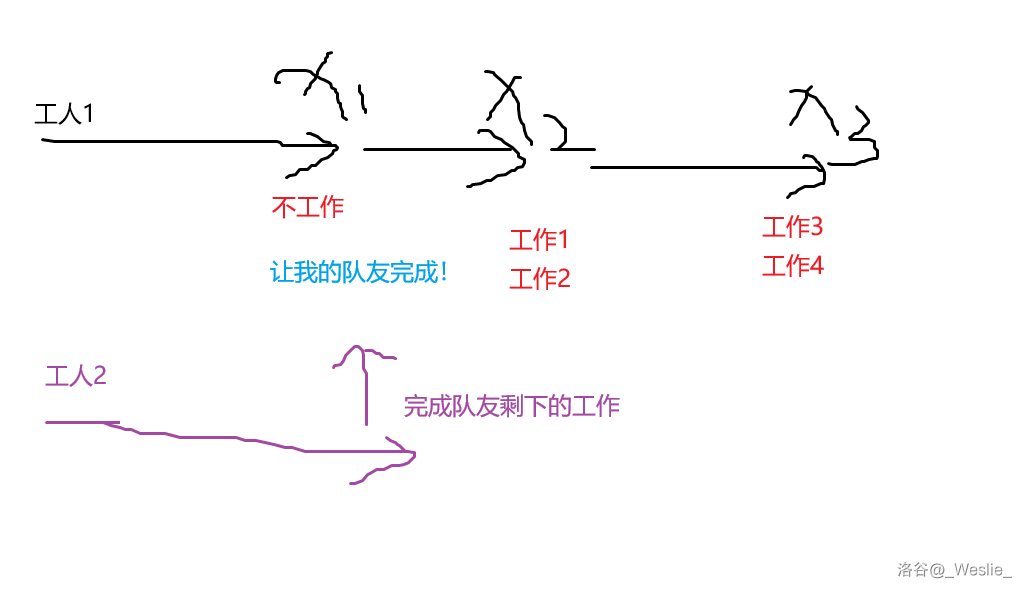
显然下面的情况，工人 22 走的路程更少，显然更优。
有人可能会说，万一工人 11 自己处理 x2x_2 位置的工作就超时了。其实这样的话，让工人 22 到 x2x_2 位置处理就可以了，显然不劣于第一种情况（工作总数和移动距离是一样的）。
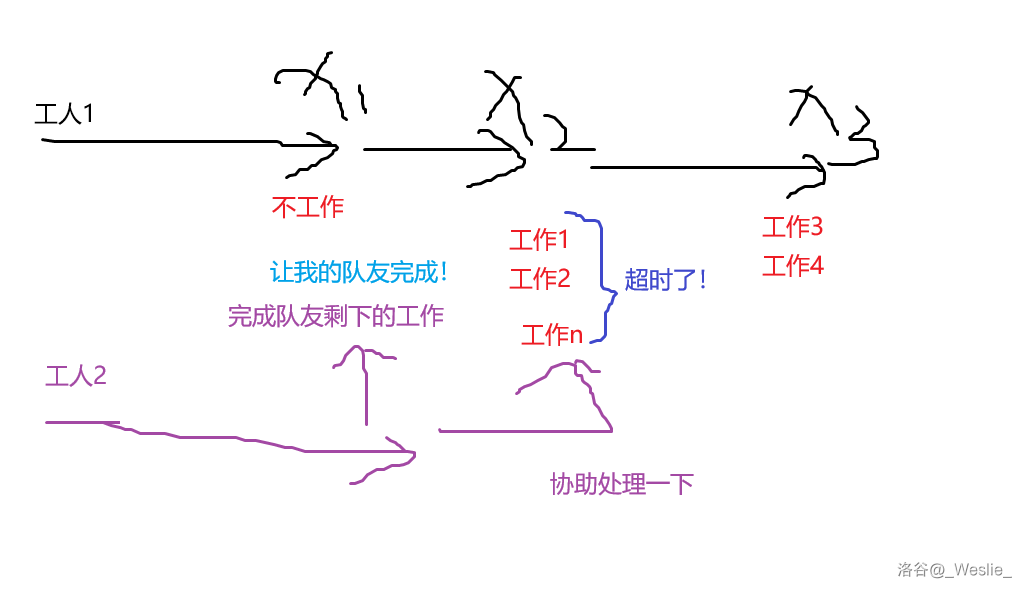
所以一个工人的工作位置必然是一段区间。
贪心问题 22
是否会出现两个工人一起走共同工作的情况？
就像这样：
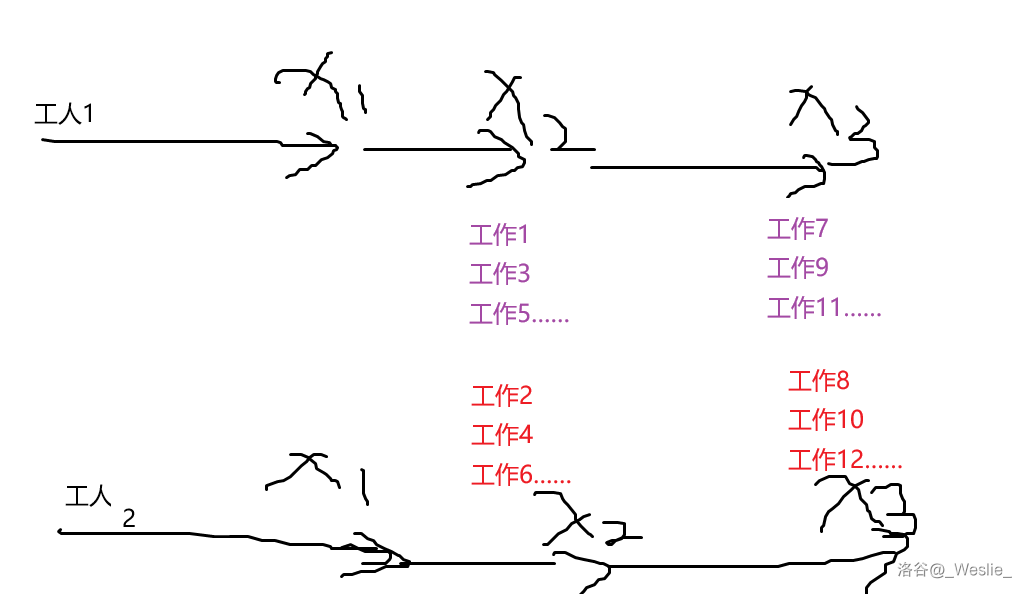
（两个人同时开始工作，同时在一个点工作，同时完成工作）
结论
不会！
因为你会发现：
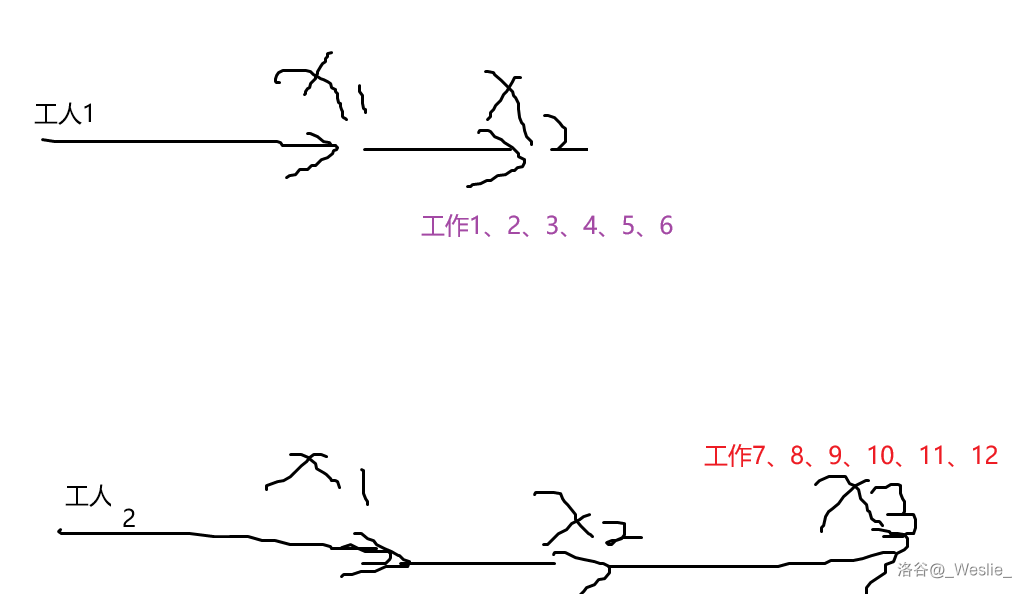
这样第一个工人无需走 [x2,x3][x_2,x_3] 这一段，显然比一开始的情况好。
贪心问题 33
当一个工人结束了某个位置的工作之后，剩余时间不足以支撑他完成下一个位置的工作，那他是就地停止还是撑到下一个位置，在有限的时间内尽可能完成自己的工作呢？
结论
很显然的结论：你还是尽量让他多干点活。
最后我们得到了一个贪心策略：模拟某个工人的过程，如果多这个位置不会超时（上一个位置 lstlst 到这里 bib_i 的和加上这个位置 aia_i 的和 ≤t\le t），那么就干完这个位置的活；否则就尽自己所能（看看走到这个位置剩多久干多久的活）干点活为其他工人提供便利。
但是有可能有些位置任务实在太多了，导致很多工人只在这个点上干活都干不完。这样的情况我们加一个特判就能解决：考虑工人走到这个位置（前面什么都不干之后剩余时间为 rr），上一个工人干完之后这个位置剩余 ww 个任务，那么只需再安插 ⌊wr⌋+1\lfloor \dfrac{w}{r}\rfloor+1 个工人即可。注意这个 +1+1，他可以去下一个位置干活。所以这时要更新 lstlst。
注意边界：如果第 nn 个位置 w mod r=0w\bmod r=0，那么你无需为了下一个位置再安排一个工人，就不需要 +1+1 了。
由于某些工人干活的过程中，一些位置的 bib_i 会改变，所以需要用树状数组维护 bib_i 的和，复杂度 O⁡(nlog⁡nlog⁡V)\operatorname{O}(n\log n\log V)。其实也可以维护一个变量表示这个工人消耗了多少时间，也不难写，这样复杂度是 O⁡(nlog⁡V)\operatorname{O}(n\log V)。
O⁡(nlog⁡nlog⁡V)\operatorname{O}(n\log n\log V) 的代码CPP
#include<bits/stdc++.h>
#define ll long long
#define fi first
#define se second
#define fastio ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define ls (now<<1)
#define rs ((now<<1)|1)
#define int long long
using namespace std;
const int N=200005;
ll a[N],b[N],sum[N]; 
int n,m;
struct bittree{
	ll tr[N];
	int lowbit(int x){
		return x&(-x);
	}
	void init(){
		memset(tr,0,sizeof tr);
	}
	void update(int now,ll x){
		while(now<=n){
			tr[now]+=x;
			now+=lowbit(now);
		}
	}
	ll qsum(int now){
		ll res=0;
		while(now){
			res+=tr[now];
			now-=lowbit(now);
		}
		return res;
	}
	ll query(int l,int r){
		return qsum(r)-qsum(l-1);
	}
}tr; 
bool check(ll t){
	int lst=1,cnt=0;
	tr.init();
	for(int i=1;i<=n;i++){
		tr.update(i,b[i]);
	}
	cnt=1;
	for(int i=1;i<=n;i++){
		if(a[i]+tr.query(lst,i)>t){
			ll r=(t-(a[i]+tr.query(lst,i-1)));
			if(r>0)tr.update(i,-r);
			if(tr.query(i,i)){
				r=t-a[i];
				if(r<=0)return false;
				ll w=tr.query(i,i);
				cnt+=w/r;
				tr.update(i,-(w/r*r));	
				lst=i;
				if(i!=n||tr.query(i,i)!=0)cnt++;
			}
		}
	}
	return cnt<=m;
}
signed main(){
//	freopen(".in","r",stdin);
//	freopen(".out","w",stdout);
	fastio;
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		cin>>a[i];
	}
	for(int i=1;i<=n;i++){
		cin>>b[i];
		tr.update(i,b[i]);
	}
	ll l=1,r=1000000000000000000,ans=0;
	while(l<=r){
		ll mid=(l+r)>>1;
		if(check(mid)){
			ans=mid;
			r=mid-1;
		}
		else l=mid+1;
	}
	cout<<ans<<'\n';
	return 0;
}

评论

共 0 条评论，欢迎与作者交流。

正在加载评论...