专栏文章
题解:P5998 [PA 2014] Plemiona
P5998题解参与者 1已保存评论 1
文章操作
快速查看文章及其快照的属性,并进行相关操作。
- 当前评论
- 1 条
- 当前快照
- 1 份
- 快照标识符
- @mio6vtsb
- 此快照首次捕获于
- 2025/12/02 14:20 3 个月前
- 此快照最后确认于
- 2025/12/02 14:20 3 个月前
因为是最优解所以写一个。
前置知识:颜色段均摊,启发式合并。
看完题发现数据不好造,考虑乱搞。
通式扫描线,考虑按上边界从低到高扫,用一个颜色段均摊维护当前每个位置上最高的矩形。每次这样就可以方便地维护横坐标与当前插入的矩形相交的有哪些矩形。
注意相交的定义
本题中,相交部分面积严格大于 才算相交。实现时可以将所有矩形的右边界和上边界分别缩一个单位长度,让相交的定义变成有点相交。
然后考虑现在取出了若干个和当前矩形横坐标上有交的矩形。如果纵坐标也有交的话,两个矩形就将合并。合并是容易的,对四个边界分别取极值作为新边界即可。
合并过程中,使用并查集维护“每种颜色现在对应哪个矩形”,这样可以减少对颜色段均摊的修改。
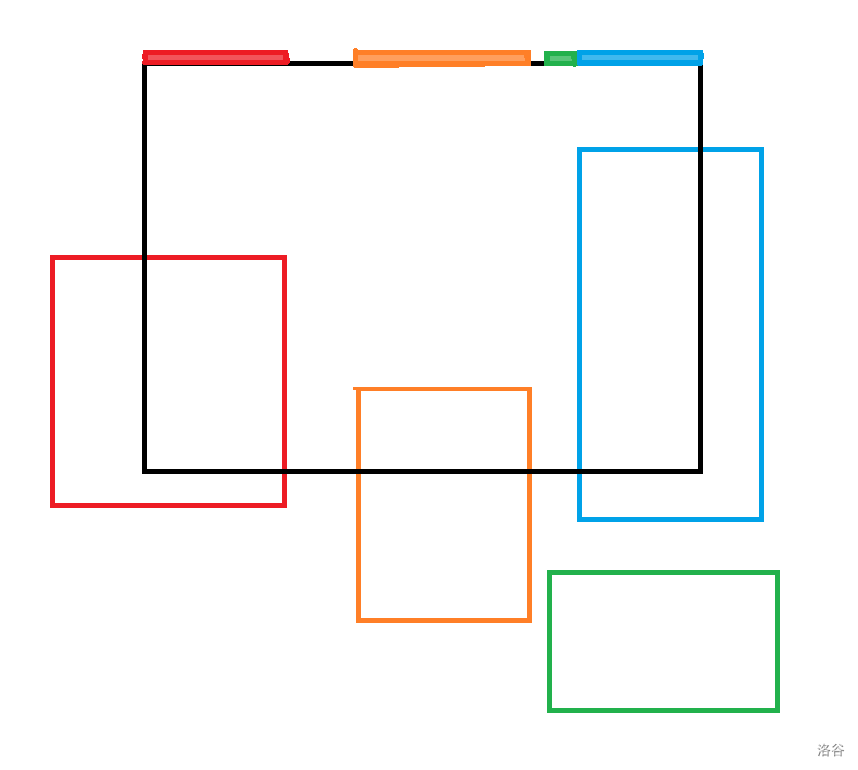
如图,插入黑色矩形时,将会检定与它相交的红橙绿蓝四个颜色段,其中红橙蓝三个矩形会直接与之合并。
CPPstruct Node{
mutable int l,r,v;
bool operator<(const Node&p)const{return l<p.l;}
};
struct ODT:set<Node>{
#define iter ODT::iterator
int n;void init(int _n){insert({0,n=_n,0});}//0 表示没有被覆盖过
iter _find(int x){return prev(upper_bound({x,0,0}));}
iter spilt(int x){
if(x>n)return end();
iter it=_find(x);
if(it->l==x)return it;
int l=it->l,r=it->r,v=it->v;
erase(it),insert({l,x-1,v});
return insert({x,r,v}).x;
}
void assign(int l,int r,int v){
iter itr=spilt(r+1),itl=spilt(l);//找到和 [l,r] 有交的颜色段区间
for(iter it=itl;it!=itr;erase(it++))
if(it->v&&::find(it->v)!=::find(v))::merge(v,it->v);//尝试合并
insert({l,r,::find(v)});//颜色段均摊标准操作
}
#undef iter
}odt;
如果纵坐标没有交的话,直接将这一个颜色段覆盖掉,会出现这样的问题:
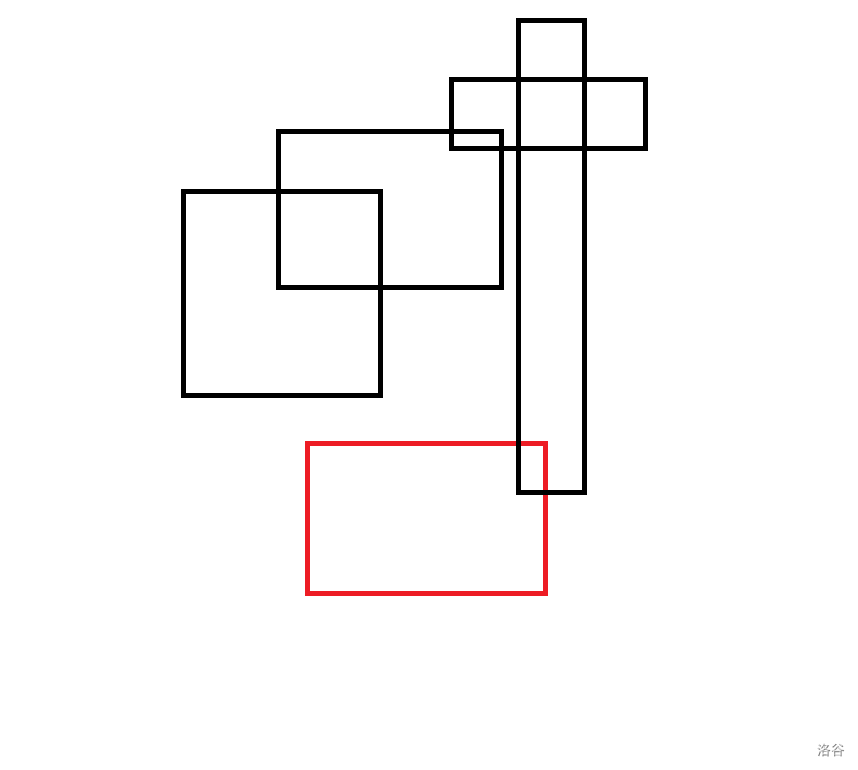
如图,红色矩形被三个更高的黑色矩形完全覆盖,最后插入那个很长的黑色矩形时,不能在维护颜色段均摊的数据结构上找到红色矩形并合并。
因为颜色段均摊的优秀性质,可以直接在覆盖颜色时,从高的矩形向低的矩形连一条出边,表示“这两个矩形横坐标相交,纵坐标暂时不相交,但是如果高的矩形在扫描线过程中与别的矩形合并了,纵坐标就有可能相交”。
使用
std::set 存储,动态将所有出边按照矩形上边界从高到低排序,那每次合并时检定最高的若干个出边并合并,就可以保证复杂度正确。比如说上图中,前三个黑色矩形会合并成一个大矩形,它的出边包含红色矩形。大矩形与细长黑色矩形合并时,这条出边会被检定,这样就不会漏掉红色矩形了。
为什么不需要考虑那个什么情况?
排序时不需要考虑“较低的矩形与其他矩形合并之后变高”的情况,它不影响合并的正确性与复杂度,原因容易证明:如果较低的矩形在扫描线过程中的“未来”变高了,那它变高之后必然会穿过我们当前考虑的较高的矩形,到时候必定要合并这两个矩形。在下面的流程中,这种情况一定不会被漏掉。
那个什么情况也不用吗?
维护一些冗余的出边(比如两个矩形已经被合并过了,或者一个矩形被添加多次)不会让复杂度变劣。冗余出边的影响是容易用并查集处理的。
合并两个矩形后,记得将出边集合也一并合并,可以使用启发式合并实现。
CPPint fa[N];
int find(int x){return fa[x]==x?x:fa[x]=find(fa[x]);}
struct Info{
int l,r,u,d;
}w[N],res[N];
set<pii,greater<pii>>t[N];
bool chk(int l,int r,int l0,int r0){//check 两个区间是否有交
if(l>l0)swap(l,l0),swap(r,r0);
return l0<=r;
}
bool chk(Info a,Info b){//check 两个矩形是否有交
return chk(a.l,a.r,b.l,b.r)&&chk(a.d,a.u-1,b.d,b.u-1);
}
void merge(int u,int v){
if(u=find(u),v=find(v);u==v)return;
if(w[u].d<w[v].d)swap(u,v);//将深的矩形合并到浅的矩形上,以减少分类讨论
if(!chk(w[u],w[v]))//加出边
return t[u].insert(pii(w[v].u,v)),void();
vector<int>vt;
fa[v]=u,
chkmn(w[u].l,w[v].l),chkmx(w[u].r,w[v].r),
chkmn(w[u].d,w[v].d),chkmx(w[u].u,w[v].u);
for(auto it=t[u].begin();it!=t[u].end();t[u].erase(it++)){
if(w[find(it->y)].u<=w[v].d)break;//考虑到可能在懒惰合并期间发生了别的合并,判定时需要先 find
if(find(u)!=find(it->y))vt.pb(it->y);//检定出边中最高的若干个矩形,如果有交,也即出边矩形的上边界高于当前矩形的下边界,就合并进当前矩形
}
for(auto it=t[v].begin();it!=t[v].end();t[v].erase(it++)){//理论上这个循环会直接退出
if(w[find(it->y)].u<=w[v].d)break;
if(find(u)!=find(it->y))vt.pb(it->y);
}
if(t[u].size()<t[v].size())swap(t[u],t[v]);//启发式合并剩余的出边
for(pii p:t[v])t[u].insert(pii(w[find(p.y)].u,p.y));
for(int nv:vt)merge(u,nv);//将刚才拿出来的出边递归合并
}
因为是模拟赛期间实现的,所以没有那么精细,一些合并操作是明显冗余的。无论如何,它目前都是最优解。
然后回到刚才的问题,合并完一轮之后,当前矩形的宽度和高度都可能增加。因为颜色段均摊的优秀性质,将当前矩形直接重新再加入一次是没有问题的。是的,它会访问到刚刚插入的表示当前矩形的颜色段,但是这也只有一个。
所以重复插入直到矩形不再扩张为止。
CPP for(int i=1;i<=n;i++)
if(w[i].l<=--w[i].r&&w[i].d<w[i].u){//模拟赛的题面说可能有矩形退化成线,所以加了判断,实际上可能并没有这样的数据
int l,r,u,d;
R://需要注意的是,并查集合并了若干轮之后,并查集的根可能不是 i
l=w[find(i)].l,r=w[find(i)].r;
u=w[find(i)].u,d=w[find(i)].d;
odt.assign(w[find(i)].l,w[find(i)].r,find(i));
if(auto[_l,_r,_u,_d]=w[find(i)];
l!=_l||r!=_r||u!=_u||d!=_d)
goto R;
}
时间复杂度:根据颜色段均摊的结论,操作的区间数量关于操作次数成线性。如果认为总共出边集合大小是 级别的,那么瓶颈在启发式合并,复杂度不高于 ;实践上常数极小。可能可以分析出更低的复杂度。
full code
CPP#include<bits/extc++.h>
#include<bits/stdc++.h>
//#pragma GCC optimize(2)
//This code contains niche emotional elements. It is recommended to watch it after the age of 18.
#ifdef __unix__
#define gc getchar_unlocked
#define pc putchar_unlocked
#else
#define gc _getchar_nolock
#define pc _putchar_nolock
#endif
#ifdef local
#define fileio(x,y) freopen(#x"/"#x#y".in","r",stdin),freopen(#x".out","w",stdout);
#else
#define fileio(x,y) freopen(#x".in","r",stdin),freopen(#x".out","w",stdout);
#endif
#define debugline fprintf(stderr,"--------------------------\n")
#define debug(x) fprintf(stderr,"Line %d,%s=%lld\n",__LINE__,#x,(ll)(x))
#define dbgln0 fprintf(stderr,"------------- What is mind? No matter. -------------\n")
#define dbgln1 fprintf(stderr,"============= What is matter? Never mind. =============\n")
#define all(x) x.begin(),x.end()
#define min(args...) min({args})
#define max(args...) max({args})
#define pii pair<int,int>
#define Inf (int)INFINITY
#define ldb long double
#define inf 0x3f3f3f3f
#define i128 __int128
#define pb push_back
#define ll long long
#define db double
#define endl '\n'
#define y second
#define x first
using namespace std;
const int N=1e5+10;
mt19937 rnd(20071020);
template<typename T>inline void chkmn(T&a,const T&b){a=min(a,b);}
template<typename T>inline void chkmx(T&a,const T&b){a=max(a,b);}
void read(){};
template<class T1,class...T2>
inline void read(T1&ret,T2&...rest){
ret=0;char c=gc();bool f=0;
for(;!isdigit(c);c=gc())f=c=='-';
for(;isdigit(c);c=gc())ret=ret*10+c-'0';
f&&(ret=-ret),read(rest...);
}
#define cin(...) read(__VA_ARGS__)
template<class T>
inline void print(T x){
static short s[35],t=0;
bool f=x<0;if(f)x=-x;
do s[t++]=x%10,x/=10;while(x);
for(f&&pc('-');t;)pc(s[--t]+'0');
}
int fa[N];
int find(int x){return fa[x]==x?x:fa[x]=find(fa[x]);}
struct Info{
int l,r,u,d;
}w[N],res[N];
set<pii,greater<pii>>t[N];
int n,m,V;
bool chk(int l,int r,int l0,int r0){
if(l>l0)swap(l,l0),swap(r,r0);
return l0<=r;
}
bool chk(Info a,Info b){
return chk(a.l,a.r,b.l,b.r)&&chk(a.d,a.u-1,b.d,b.u-1);
}
void merge(int u,int v){
if(u=find(u),v=find(v);u==v)return;
if(w[u].d<w[v].d)swap(u,v);
if(!chk(w[u],w[v]))
return t[u].insert(pii(w[v].u,v)),void();
vector<int>vt;
fa[v]=u,
chkmn(w[u].l,w[v].l),chkmx(w[u].r,w[v].r),
chkmn(w[u].d,w[v].d),chkmx(w[u].u,w[v].u);
for(auto it=t[u].begin();it!=t[u].end();t[u].erase(it++)){
if(w[find(it->y)].u<=w[v].d)break;
if(find(u)!=find(it->y))vt.pb(it->y);
}
for(auto it=t[v].begin();it!=t[v].end();t[v].erase(it++)){
if(w[find(it->y)].u<=w[v].d)break;
if(find(u)!=find(it->y))vt.pb(it->y);
}
if(t[u].size()<t[v].size())swap(t[u],t[v]);
for(pii p:t[v])t[u].insert(pii(w[find(p.y)].u,p.y));
for(int nv:vt)merge(u,nv);
}
struct Node{
mutable int l,r,v;
bool operator<(const Node&p)const{return l<p.l;}
};
struct ODT:set<Node>{
#define iter ODT::iterator
int n;void init(int _n){insert({0,n=_n,0});}
iter _find(int x){return prev(upper_bound({x,0,0}));}
iter spilt(int x){
if(x>n)return end();
iter it=_find(x);
if(it->l==x)return it;
int l=it->l,r=it->r,v=it->v;
erase(it),insert({l,x-1,v});
return insert({x,r,v}).x;
}
void assign(int l,int r,int v){
iter itr=spilt(r+1),itl=spilt(l);
for(iter it=itl;it!=itr;erase(it++))
if(it->v&&::find(it->v)!=::find(v))::merge(v,it->v);
insert({l,r,::find(v)});
}
#undef iter
}odt;
signed main(){
cin(n),iota(fa+1,fa+n+1,1);
for(int i=1,l,r,d,u;i<=n;i++)
cin(l,r,d,u),w[i]={l,r,u,d},chkmx(V,r);//我习惯于将 d 设为较小的值,因此交换了一下
sort(w+1,w+n+1,[&](Info a,Info b){
return a.u^b.u?a.u<b.u:a.l<b.l;
});
odt.init(V);
for(int i=1;i<=n;i++)
if(w[i].l<=--w[i].r&&w[i].d<w[i].u){
int l,r,u,d;
R:
l=w[find(i)].l,r=w[find(i)].r;
u=w[find(i)].u,d=w[find(i)].d;
odt.assign(w[find(i)].l,w[find(i)].r,find(i));
if(auto[_l,_r,_u,_d]=w[find(i)];
l!=_l||r!=_r||u!=_u||d!=_d)
goto R;
}
for(int i=1;i<=n;i++)
if(find(i)==i)res[++m]=w[i],res[m].r++,swap(res[m].u,res[m].d);
print(m),pc(endl);
sort(res+1,res+m+1,[&](Info a,Info b){
return make_tuple(a.l,a.r,a.u,a.d)<make_tuple(b.l,b.r,b.u,b.d);
});
for(int i=1;i<=m;i++)
print(res[i].l),pc(' '),print(res[i].r),pc(' '),print(res[i].u),pc(' '),print(res[i].d),pc(endl);
// for(int i=1;i<=m;i++){
// if(res[i].l==res[i].r||res[i].u==res[i].d)continue;
// for(int j=1;j<i;j++){
// if(res[j].l==res[j].r||res[j].u==res[j].d)continue;
// if(chk(res[i].l,res[i].r-1,res[j].l,res[j].r-1)&&
// chk(res[i].u,res[i].d-1,res[j].u,res[j].d-1)){
// cerr<<i<<" "<<j<<endl;
//// assert(0);
// }
// }
// }
return 0;
}
相关推荐
评论
共 1 条评论,欢迎与作者交流。
正在加载评论...