题解：P5399 [Ynoi2018] 駄作

前置知识: Top cluster 树分块

1. $u$ 是根节点。
2. $u$ 有超过两个子树内有界点（如果 $u$ 不是界点则违背了一个簇中最多有两个界点的限制）。
3. 删去 $u$ 子树中的界点以及界点的子树后，剩下点的数量超过了 $B$。

1. 加入新子树的未划分点后，$S$ 的大小将会大于 $B$。
2. 加入新子树的未划分点后，$S$ 将会有多于 $1$ 个下界点，违背了条件。
3. 在先前我们没有处理 $u$ 的任意子树。

1. 一个簇中最多有两个界点，一个簇外的点到达簇内的点必须经过这两个点的其中一个。
2. 一个簇的上界点是这个簇中深度最小的点，这极大地简化了某些计算问题。
3. 由于（2）的特性，我们可以建立一棵收缩树，将每一个簇的上界点和下界点连边，这一棵树的大小是 $O(\frac{n}{B})$ 的，很适合我们进行计算。

Solution

1. 不同簇之间的贡献。由于两个簇中的点之间的路径经过固定的点，我们可以在收缩树上进行树形DP来统计贡献，考虑当前点是 $u$：
   1. 点 $x$ 和点 $y$ 的贡献：我们可以预处理出点 $x$ 到 $x$ 所属簇下界点的距离 $dl_x$，因此 $x$ 到 $y$ 的距离可以写成 $dl_x + dep_y - dep_u$。
   2. 点 $y$ 和点 $z$ 的贡献：可以写成 $dep_y + dep_z - 2dep_u$。
   因此，我们可以处理对于每一个块，两个点对应的邻域的大小，深度和，到下界点的距离和就可以转移了，这里总共的时间复杂度是 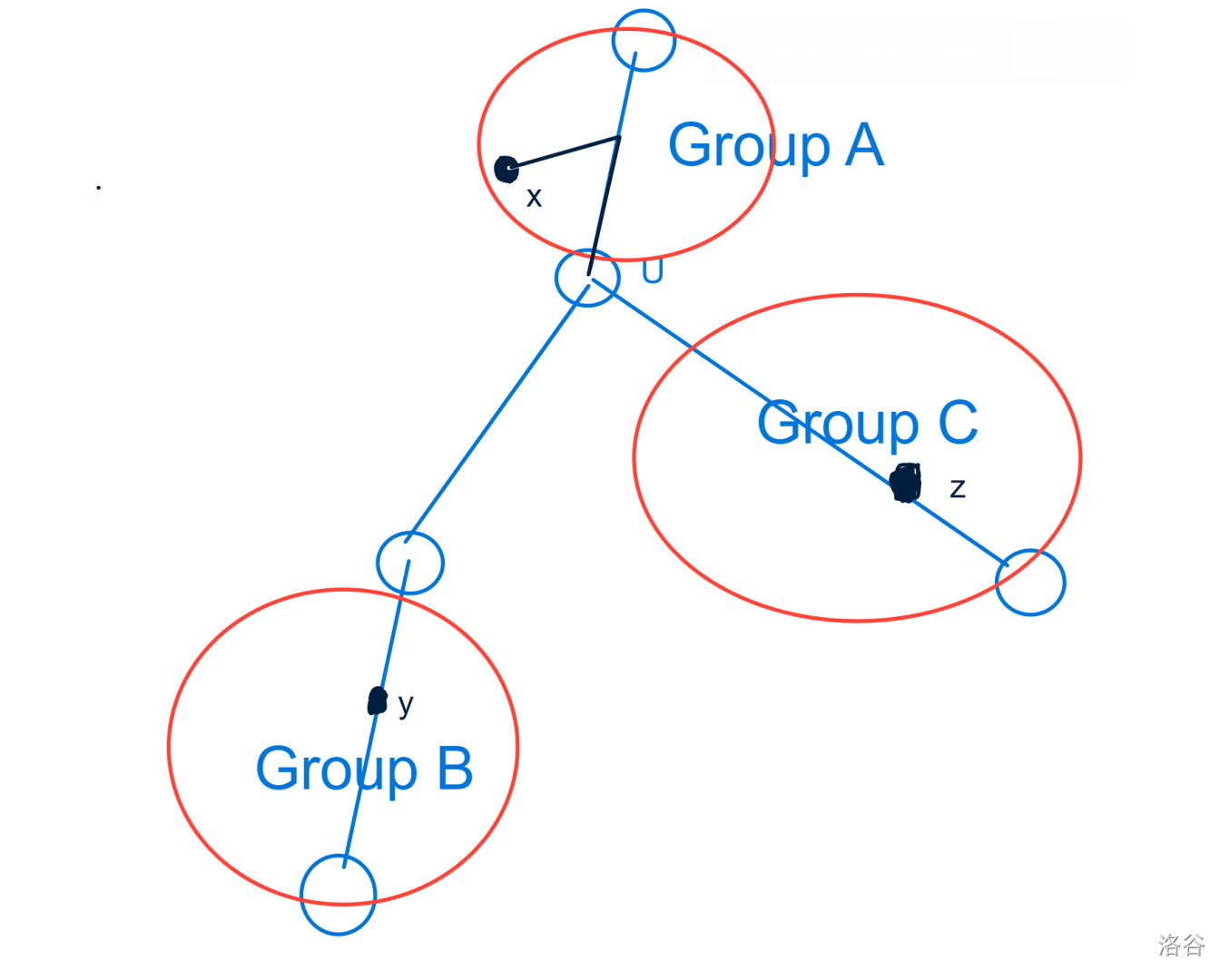$O(m (B + \frac{n}{B}))$。
2. 一个簇内两个邻域之间的贡献，并且两个邻域的中心都是界点，考虑对于每一个块预处理所有的答案，$f_{0/1,0/1,i,j}$ 表示第一个邻域是以上/下界点为中心，半径为 $i$，第二个邻域是以上/下界点为中心，半径为 $j$，暴力统计即可，每一块的时间复杂度是 $O(B^2)$，需要做二维前缀和，这里的时间复杂度为 $O(\frac{n}{B}(B^2 + m))$
3. 一个簇内两个邻域之间的贡献，两个邻域的中心至少一个不是界点，对于对于每一个询问只会有 $O(1)$ 个块会这样，因此 $O(B)$ 地计算，考虑拆贡献 $dist(a,b) = dep_a + dep_b - 2 dep_{LCA(a,b)}$，前两项统计是容易的，后一项可以对于第一个邻域每个点到根（这里是上界点）的路径 $+1$，查询第二个每一个点到上界点的路径和，可以较为轻松的做到 $O(B)$ 处理。这里的时间复杂度是 $O(mB)$。

Optimization

1. 块长取 $B = 2\sqrt{n}$ 比较优秀。
2. 合理调整多维数组的顺序。
3. 这里需要 $O(1)$ 求 $dist(a,b)$，这个东西很慢，我们可以考虑预处理出每一个簇内的点到上下界点的距离，减少调用 $dist(a,b)$ 的次数。
4. 避免使用 DFS，改成循环效率更高。
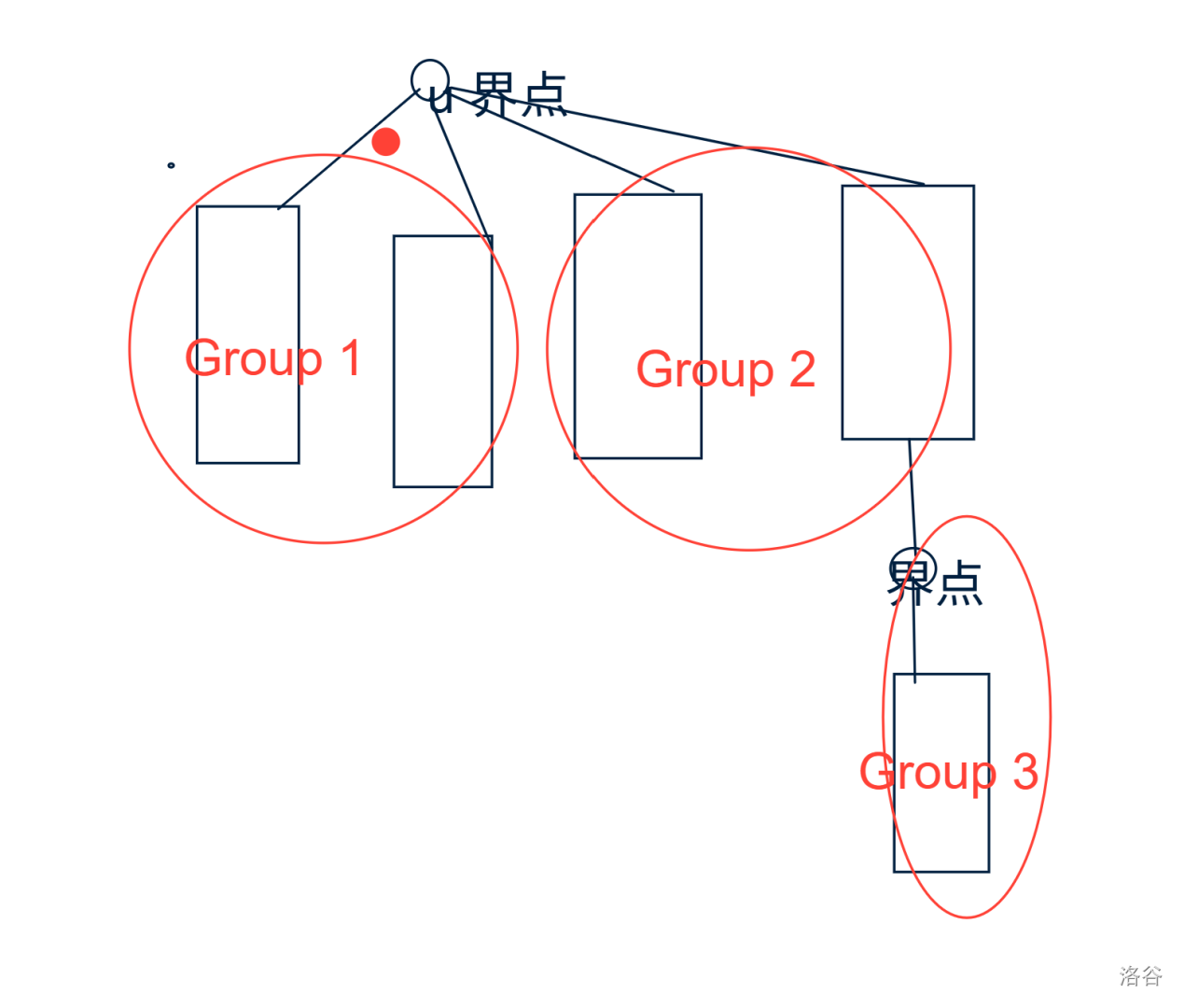
5. 尝试找到一种顺序，使其是原树的dfs序，并且每一个簇的访问是连续的，这可以考虑在做 Top Cluster 的时候“以任意顺序遍历子树”改成先遍历没有界点的子树，后遍历有界点的子树，这样就可以了，可以看图理解一下。

Code

代码常数较大，极限卡过仅供参考 查看代码。