星洒姐姐可爱

何时才能知晓自己也是美丽的呢

NOI2024 补的最后一道题，也是思维难度相当大的一道题，代码难度也不低。

题目大意

给定简单有向图

G = (V,\,E)

，对于

\forall u \in V

进行分类：

$u$ 是一类点：则 $u$ 到所有其它结点都恰好有一条简单路径。
$u$ 是二类点：可以通过删边使得 $u$ 成为一类点，并且没有一类点在删边后失去一类点的特性。
$u$ 是三类点： $u$ 不是一类点且不是二类点。

首先是暴力二进制枚举判定，期望得分

5

，对于本题做法无提示作用。

接下来我们默认有向图

G

弱连通，否则所有点均为三类点。

首先注意到一类点和二类点之间是两两可以互相到达的，符合 SCC 的定义，所以它们肯定都在一个 SCC 中；另一方面，它们能到达所有其它结点，因此它们一定是 SCC 构成的 DAG 中唯一一个入度为

0

的 SCC（如果有多个入度为

0

的 SCC，那么所有结点都是三类点）。

我们不妨把唯一一个入度为

0

的 SCC 称为『根 SCC』。

首先根 SCC 外的结点都是三类点，这点是很显然的，它们无法到达根 SCC 中的任何一个结点。

现在我们可以直接秒掉 A 性质了，如果不存在一类点，那么根 SCC 的所有点均为二类点（没有一类点来牵制我们，于是我们可以直接构造叶向树形图），时间复杂度 $\Theta(n + m)$ ，期望得分 $10$ 。

接下来来考虑性质 B，我们肯定要知道怎么判断

1

类点。

我们的条件只是不能存在两条以上简单路径，而存在多条只能经过重复结点的路径是可以被允许的。直接考虑有向图根本想象不出来怎么做，我们不妨考虑“根”出发的 DFS 树，想象在它上面从根开始找到

u

简单路径的过程。

如果我们走了一个横叉边找到简单路径，那么首先我们树边就可以到达

u

，那么一定出现了第二条简单路径，

u

必然不是一类点。

另一方面，我们如果不走横叉边，寻找

u

的过程中是不会走返祖边的，因为我们走返祖边必然会经过重复结点，此时我们只能走树边，自然而然只有一条简单路径。

也就是说，返祖边不会对根是否是一类点产生影响，而一旦存在横叉边那么根一定不是一类点。于是我们只需要在 DFS 树上判断是否存在横叉边，即可判断根是否是 $1$ 类点。

接下来我们有两个待解决的问题，一个是一类点存在的情况下二类点的形态，另一个是优化我们判断的复杂度。

不妨先优化我们判断一类点的复杂度，首先如果已知一个一类点，考虑从它开始建立 DFS 树，首先一类点为根的 DFS 树只有返祖边，我们考虑在这棵树里面想要有与所有其它结点唯一的简单路径，需要满足什么条件。

对于树边 $fa_v \to v$ ，不能被返祖边所代表的路径覆盖两次及以上，否则我们可以通过 $v$ 走两条不同的返祖边到 $fa_v$ ，走出 $v$ 到 $fa_v$ 的两个简单路径。

根据这个结论，如果

u

要是一类点，则覆盖

fa_u \to u

的返祖边至多只有一个，于是我们可以跳这个唯一的返祖边（假设它是

u \leadsto x \to y

，

x

在

u

子树中），并且断言

u

是一类点当且仅当

y

是一类点。

看起来有向 DFS 树，且没有横叉边这个性质无敌好，可以继续考虑二类点在 DFS 树上是怎么样的。

根据定义，二类点就是删边之后，我们的所有一类点仍然是一类点，而它变成一类点。

仿照求一类点的方法，我们递推来求出二类点，下面假设要判断的点都已经被判断为不是一类点。

首先不可能删树边，然后有一些返祖边也不能删，不能删的返祖边就是对于我们已经求出的一类点来说唯一覆盖它的返祖边。其余的返祖边都是可以删的。

如果没有不可删返祖边覆盖 $fa_u \to u$ ，则我们在 $u$ 子树中找返祖边（反正对于 $u$ 来说都是可删返祖边），使得该返祖边到达的点是一类点或者二类点，那么 $u$ 就是二类点。
如果恰好一条不可删返祖边覆盖 $fa_u \to u$ ，那么就只能走这条不可删返祖边。
注意以上默认删去了所有无关的覆盖 $fa_u \to u$ 的可删返祖边。
如果有两条以上的不可删返祖边覆盖 $fa_u \to u$ ，则 $u$ 完全不可能成为一类点，可以直接断言 $u$ 是三类点。

现在我们已经有了

\Theta(nm)

的做法，瓶颈在于最开始寻找一个一类点。结合 A 性质，C 性质，期望得分

55

。

怎么在最开始找到一个一类点？

这个问题事实上并不简单，对于

\Theta(n + m)

的目标复杂度来说更是困难，我们可以做线性对数的复杂度。

现在考虑广义串并联图方法。

若当图 $G,\,|V| > 1$ 存在一类点，则一定存在一个点入度为 $1$ 。

我们直接把那个一类点拿出来，以它为根的 DFS 树的叶子结点必须入度为

1

，不然根一定不是一类点。而且任意时刻我们删除了一个叶子结点，那么新产生的叶子结点也必然满足这个特性，因为我们只有返祖边而没有横叉边。那么直接拓扑排序就行！

如果你大喜过望直接写了个拓扑上去大概率会当场爆炸。

原因是因为我们的做法还有问题没有解决：

我们删点之后得到的根一定是原图的根吗？

很显然不一定，我们如果直接删点，那么是有可能把一些不应该成为一类点的点，错判为一类点的，所以我们需要在删点的同时保留被删点的出边，合并到唯一连向它的点上。这是集合的合并，可以用任意方法来做。

最后将原图删成一个点，我们就认定唯一的那个点就是一个合法的一类点。

如果可能的一类点都是一度点，我们把一度点合并掉了，找不到一类点来当根了怎么办？

我们假设根是一度点

t

，根据一类点的定义，我们可以从

t

开始走到

t

唯一入边对应的结点

p

，并且

t \leadsto p

有且只有一条简单路径。于是

p \to u

和

u \leadsto p

构成了一个简单环。我们找出

t

在这个简单环上的后继

s

，首先

s

一定是一类点（环内的点就走环，环外的点先走到

u

然后就随便走了，由于

u

是一类点，显然上述路径都是唯一的）。

那么只有两种情况。

$s$ 不是一度点，此时我们就找到了一个合法的不会被删除的根。
$s$ 是一度点，这时候我们继续在环上走下去，直到 $1$ 情况出现，或者我们走一圈走回 $t$ 了。如果我们最后走回了 $t$ ，我们得到这个简单环上的每个点都是一类点，我们直接把这个环缩在一起。根据一类点性质，缩完环之后，我们从环开始跑 DFS 树，这个 DFS 树也还是没有横叉边！注意环上结点 $u$ 的某一子树内是不会存在连向除了 $u$ 之外的环上结点的，否则原图没有一类点，同理环自己内部不存在额外边。

我们的有向图就会是这样一个非常色的结构：

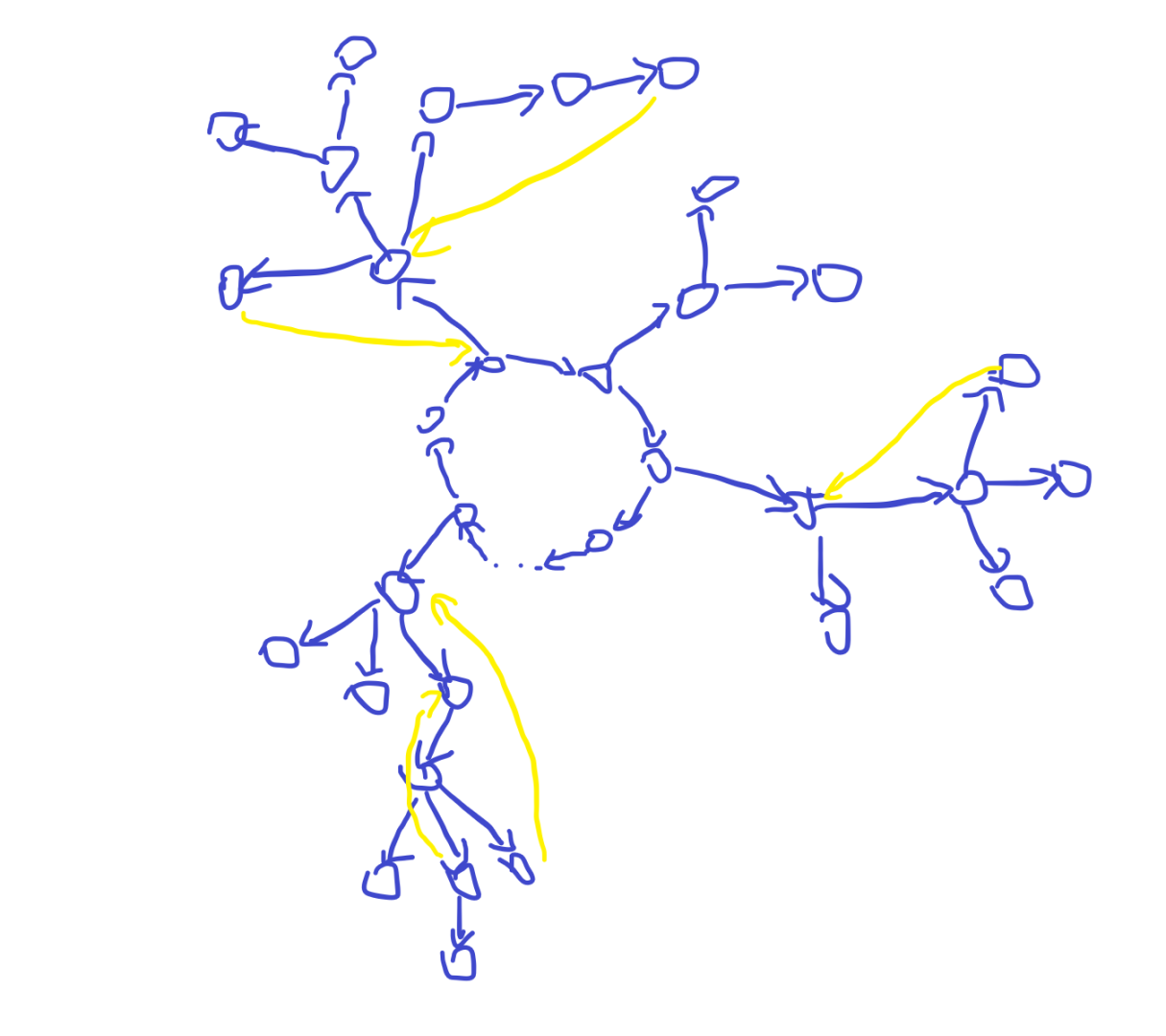
如果我们在上面缩一度点，环完全可以等价看作一个一类点，于是我们可以通过缩一度点找到一类点。

时间复杂度

\Theta((n + m) \log n)

，瓶颈在于集合合并。

接下来考虑代码实现问题。

首先求强连通分量是必须的，我们得留个后手防止不存在一类点，这时候根 SCC 就全是二类点。

至于判断一类点是否存在，就是找根的过程，找根就是不断合并一类点。

不过接下来我们要考虑合并过程中产生的重边和自环的问题，谁需要保留谁需要删。

注意到重边需要保留（否则无法区分横叉边和树边），而自环需要删除（否则合并在我们缩完点后无法继续）。

这点我们可以在每个点维护一个出边到达的点的可重集合，需要做集合的单点插入和删除，并且维护所有入度为

1

的点搞一个类似拓扑排序的玩意。

集合的合并可以写线段树合并。

然后就是一二类点的递推。

对于一类点的递推来说，我们维护覆盖

fa_u \to u

的唯一返祖边是什么，这点可以简单树上差分维护，此时

u

的一类点状态就跟这个返祖边指向的点的一类点状态相同。

如果

u

是一类点，我们还要记录这条唯一的返祖边，标记为不可删返祖边。

接下来考虑二类点们，根据我们的结论，如果两条以上不可删返祖边覆盖

fa_v \to v

，那么

v

只能是三类点。如果恰好一条不可删返祖边覆盖

fa_v \to v

，我们只能走这条返祖边，那么

v

可以类似一类点来递推。

否则没有不可删返祖边覆盖

fa_v \to v

，我们也可以用个树上差分，维护覆盖了

fa_v \to v

的可删返祖边集合，对于这些可删返祖边集合，我们维护它们终点的一类点和二类点个数，就可以简单 check 了。

时间复杂度

\Theta((n + m) \log n)

，实际上对寻找第一个类点的过程精细分析可以有一个

\Theta(n + m)

的做法，不过较为复杂。

总结一下这题的难点吧

想到一类点和二类点都在根 SCC 内，这点是很显然的，毕竟弱化一类点的条件，那么至少它们之间是两两有路径的，而这正是 SCC 的定义。所以 A 性质应当是不难想到的。

首先第一个难点是找到判断一类点的好的充要条件，也就是以该点为根的 dfs 树没有横叉边。这点需要不少的注意力和经验，对于连通性问题考虑 dfs 生成树一般是不劣的想法，而且这个恰好只有一条简单路径更让我们想到树的性质，类比推理大概可以想到。

第二个难点是怎么优化复杂度，你很可能直接考虑到处碰壁，都是因为无法处理横叉边，那如果我们只有返祖边你会发现问题好考虑了很多，这点就是基于我们之前得到的判断方法来做的。如果我们能先找到一个一类点当根，剩下的问题对于 NOI 级别的选手来说，是完全在能力范围内可以做到的。

个人认为最大的难点是怎么寻找第一个一类点，能注意到缩一度点这个问题是真的很不简单，至少是需要很多题目的历练和一些奇思妙想的，这应该也是这题在场上场切极少的原因之一（其实主要原因应该是~~大家都去做登山了~~）。

以下是参考代码，关键部分会有注释，当然由于是宿舍床上着急写的，所以可能有不少优化空间。

CPP

int T, n, m, dfn[maxn], low[maxn], dct, st[maxn], tp, vis[maxn], scc[maxn], N, ans[maxn], Q[maxn], rd[maxn], pa[maxn], id[maxn], c[3][maxn], hd, tl, RT;
vec<int> g[maxn], rg[maxn], h[maxn], r[maxn]; 
inline void add(int o, int x, int d) { while (x <= n) c[o][x] += d, x += x & -x; }
inline int qsum(int o, int x) { int s = 0; while (x) s += c[o][x], x -= x & -x; return s; }
struct Node { int l, r, v; } t[maxn * 20]; int rt[maxn], tot;
#define ls(x) (t[x].l)
#define rs(x) (t[x].r)
#define w(x) (t[x].v)
void mdf(int l, int r, int v, int p, int& x) {
	if (!x) x = ++tot; w(x) += p; if (l == r) return;
	v <= mid ? mdf(l, mid, v, p, ls(x)) : mdf(mid + 1, r, v, p, rs(x));
}
int qry(int l, int r, int v, int x) {
	if (!x) return 0; if (l == r) { int k = w(x); w(x) = 0; return k; }
	return v <= mid ? qry(l, mid, v, ls(x)) : qry(mid + 1, r, v, rs(x));
}
void mg(int& x, int& y) {
	if (!w(x) || !w(y)) return void(x |= y);
	else w(x) += w(y), mg(ls(x), ls(y)), mg(rs(x), rs(y));
}
void tj(int u) {
	dfn[u] = low[u] = ++dct; vis[st[++tp] = u] = 1;
	for (int v : g[u]) {
		if (!dfn[v]) tj(v), low[u] = min(low[u], low[v]);
		else if (vis[v]) low[u] = min(low[u], dfn[v]);
	}
	if (dfn[u] == low[u]) {
		++N;
		do scc[st[tp]] = N, vis[st[tp]] = 0; while (st[tp--] != u);
	}
}
int fd(int x) { return pa[x] == x ? x : pa[x] = fd(pa[x]); }
int getrt() {
	hd = 1, tl = 0;
	rep(i, 1, n) {
		if (rd[i] == 1) Q[++tl] = i;
		for (int v : g[i]) mdf(1, n, v, 1, rt[i]);
	}
	// 合并是对于 u -> v 将 v 保留出边合并到 u 上
	while (hd <= tl) {
		int v = Q[hd++], u = 0;
		if (pa[v] != v || rd[v] != 1) continue;
		for (int x : rg[v]) if (v != fd(x)) { u = fd(x); break; }
		qry(1, n, v, rt[u]);
		int k = qry(1, n, u, rt[v]);
		if (k && (rd[u] -= k) == 1) Q[++tl] = u;
		mg(rt[u], rt[v]); pa[v] = RT = u;
	}
	//cout << RT << "\n"; exit(0);
	if (tl < n - 1) return -1;
	else return RT;
}
int fr[maxn], to[maxn], sz[maxn], p; // 标号为 i 的返祖边是什么
void prework(int u, int f) {
	// 先建立以 RT 为根的 DFS 树
	dfn[u] = ++dct; sz[u] = 1;
	for (int v : g[u]) {
		if (!dfn[v]) h[u].pb(v), prework(v, u), sz[u] += sz[v];
		else {
			// 否则 u -> v 是一个返祖边，给它一个标号
			++p; fr[p] = u, to[p] = v; r[v].pb(p);
			add(0, dfn[u], 1), add(0, dfn[v], -1);
			add(1, dfn[u], p); add(1, dfn[v], -p);
			// 转到子树树上差分，接下来我们要做的就是区分可删返祖边和不可删返祖边
		}
	}
}
int FC_, GC_, FS_, ndl[maxn];  //
inline ll SUM(int o, int u) { return qsum(o, dfn[u] + sz[u] - 1) - qsum(o, dfn[u] - 1); }
void dfs1(int u) {
	// 求出所有一类点和不可删返祖边
	// 一个点 u 是一类点，当且仅当 u = RT 或 fa[u] \to u 被恰好一条返祖边覆盖，该返祖边指向的点是一类点
	// dfs1 的时候 FC_ 是当前覆盖 fa[u] \to u 的返祖边数量，FS_ 是根据差分结果得到的唯一的返祖边编号
	FC_ = SUM(0, u), FS_ = SUM(1, u);
	//if (u == 1) cout << FC_ << " " << FS_ << "\n";
	if (FC_ == 1 && ans[to[FS_]] == 1) ans[u] = 1, ndl[FS_] = 1;
	for (int v : h[u]) dfs1(v);
}
void prework_2() {
	rep(i, 1, p) {
		if (ndl[i]) {
			int u = fr[i], v = to[i];
			add(0, dfn[u], 1), add(0, dfn[v], -1);
			add(1, dfn[u], i), add(1, dfn[v], -i);
		}
	}
}
void dfs2(int u) {
	// 求出所有二类点和可删返祖边
	// 具体来说我们要求出 fa[u] \to u 被多少条不可删返祖边覆盖，这也是树上差分，如果没有被不可删返祖边覆盖，则根据我们维护的可删返祖边情况判断 u 的类型
	// 我们维护经过 fa[u] \to u 有多少个可删返祖边终点是一类点或二类点
	// 一次 dfs，两个树上差分，三个树状数组
	FC_ = SUM(0, u), FS_ = SUM(1, u), GC_ = SUM(2, u);
	if (!ans[u]) {
		//if (u == 3) cout << FC_ << " " << FS_ << " " << GC_ << "\n";
		// 判定 u 是否是二类点
		if (FC_ >= 2) ans[u] = 3;
		else if (FC_ == 1) ans[u] = (ans[to[FS_]] != 3 ? 2 : 3); // 看唯一不可删返祖边指向的点，当然我们已经排除 u 是一类点了
		else ans[u] = (GC_ > 0 ? 2 : 3);
	}
	if (ans[u] == 1 || ans[u] == 2) for (int y : r[u]) if (!ndl[y]) add(2, dfn[fr[y]], 1), add(2, dfn[u], -1);
	for (int v : h[u]) dfs2(v);
}
void clear() {
	rep(i, 1, n) rd[i] = ans[i] = dfn[i] = low[i] = st[i] = vis[i] = scc[i] = rd[i] = rt[i] = id[i] = c[0][i] = c[1][i] = c[2][i] = sz[i] = ndl[i] = 0, g[i].clear(), rg[i].clear(), h[i].clear(), r[i].clear();
	rep(i, 1, tot) t[i].l = t[i].r = t[i].v = 0; p = tot = dct = tp = N = 0;
}
void putans() { rep(i, 1, n) printf("%d", ans[i]); puts(""); clear(); }
void solve() {                                                                                                  
	scanf("%d%d", &n, &m); rep(i, 1, n) pa[i] = i;
	for (int i = 1, u, v; i <= m; i++) scanf("%d%d", &u, &v), g[u].pb(v), rg[v].pb(u), ++rd[v];
	rep(i, 1, n) if (!scc[i]) tj(i); hd = 1, tl = 0;
	rep(i, 1, n) if (scc[i] == N) Q[++tl] = i, vis[i] = 1; else vis[i] = 0; // Tarjan 得到的 SCC 编号是拓扑序逆序，Kosaraju 得到的 SCC 编号是拓扑序正序
	while (hd <= tl) { int u = Q[hd++]; for (int v : g[u]) if (!vis[v]) Q[++tl] = v, vis[v] = 1; }
	rep(i, 1, n) if (!vis[i]) { rep(j, 1, n) ans[j] = 3; putans(); return; } // 根 SCC 到不了所有结点
	RT = getrt(); // cout << RT << "\n";
	if (RT == -1) { rep(i, 1, n) ans[i] = scc[i] == N ? 2 : 3; putans(); return; } // 没有找到一类点
	rep(i, 1, n) dfn[i] = 0; dct = 0; prework(RT, 0);
	rep(i, 1, p) {
		int u = fr[i], v = to[i];
		if (dfn[u] < dfn[v] || dfn[u] + sz[u] > dfn[v] + sz[v]) RT = -1;
	}
	if (RT == -1) { rep(i, 1, n) ans[i] = scc[i] == N ? 2 : 3; putans(); return; } 
	ans[RT] = 1; dfs1(RT); FC_ = FS_ = 0; 
	rep(i, 1, n) c[0][i] = c[1][i] = c[2][i] = 0; prework_2();
	dfs2(RT); FC_ = FS_ = GC_ = 0; putans();
}
int main() {
	scanf("%*d%d", &T);
	while (T--) solve();
	return 0;
}

文章操作

题目大意

相关推荐

评论

星洒姐姐可爱