专栏文章

当树剖和倍增同时闪耀——O(log log n) LCA

wwsy_I
算法·理论参与者 17已保存评论 18

文章操作

快速查看文章及其快照的属性，并进行相关操作。

当前评论
18 条
当前快照
1 份
快照标识符
@mj5z2tla
此快照首次捕获于
2025/12/15 01:02
2 个月前
此快照最后确认于
2026/02/16 01:30
4 天前
查看原文

前置知识

倍增 LCA，树剖 LCA。

引入

众所周知，LCA（最近公共祖先）是一个很常见的算法问题，有倍增，树剖，欧拉序，dfs 序等在线做法，还有 tarjan 这种离线做法。
但是……
给定一棵树，求 LCA，要求在线，预处理时间复杂度低于 O(nlog⁡n)O(n \log n)，单次查询时间低于 O(log⁡n)O(\log n)。
那好像这些算法都不行。
就真的没有办法了吗？有的。

树剖LCA

这是一种常见的 LCA，常数很小，跑的很快。
但是查询依旧是 O(log⁡n)O(\log n) 的。
先放一个代码：
代码CPP
#include <bits/stdc++.h>
using namespace std;
const int N = 5e5 + 10;
int n, m, s, fa[N], siz[N], top[N], son[N], dep[N];
vector<int> vt[N];
bool vis[N];
void dfs1(int x, int d) {
	dep[x] = d;
	vis[x] = true;
	siz[x] = 1;
	for(int i = 0; i < vt[x].size(); i++) {
		if(!vis[vt[x][i]]) {
			fa[vt[x][i]] = x;
			dfs1(vt[x][i], d + 1);
			siz[x] += siz[vt[x][i]];
			if(siz[vt[x][i]] > siz[son[x]]) son[x] = vt[x][i];
		}
	}
}
void dfs2(int x, int tp)
{
	top[x] = tp;
	vis[x] = true;
	if(son[x]) dfs2(son[x], tp);
	for(int i = 0; i < vt[x].size(); i++) {
		if(!vis[vt[x][i]]) dfs2(vt[x][i], vt[x][i]);
	}
}
int lca(int a, int b) {
	while(top[a] != top[b]) {
		if(dep[top[a]] < dep[top[b]]) swap(a, b);
		a = fa[top[a]];
	}
	if(dep[a] < dep[b]) return a;
	else return b;
}
int main()
{
	ios :: sync_with_stdio(0);
	cin.tie(0); cout.tie(0);
	cin >> n >> m >> s;
	for(int i = 1; i <= n - 1; i++) {
		int u, v;
		cin >> u >> v;
		vt[u].push_back(v);
		vt[v].push_back(u);
	}
	dfs1(s, s);
	memset(vis, false, sizeof vis);
	dfs2(s, s);
	for(int i = 1; i <= m; i++) {
		int a, b;
		cin >> a >> b;
		cout << lca(a, b) << endl;
	}
	return 0;
}
注意到这里的 lca 函数很有暴力跳的意思啊，只不过从跳父亲节点变成了跳链顶，能否优化？

优化

先画一个图：
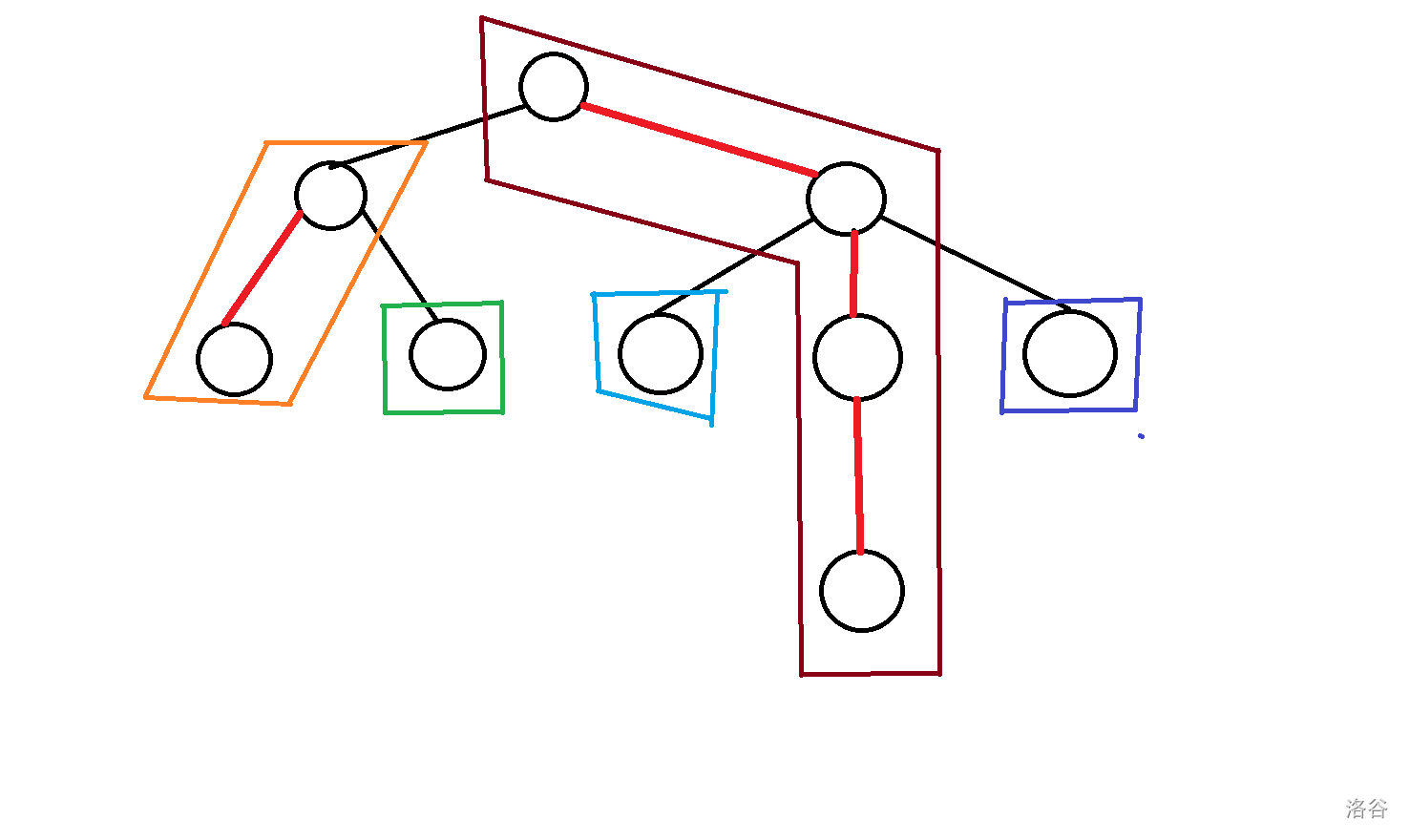
其中黑色为轻边，红色为重边，不同颜色框出了不同的重链。
跳重链的本质是什么？
其实是从一条重链上跳自己链顶的父亲，也就是跳到另一条重链上，于是我们可以想到把每一条重链缩成一个点，每一条重链的父亲就是它链顶的父亲所在的重链。比如说上面的图，我们就可以转化成这样：
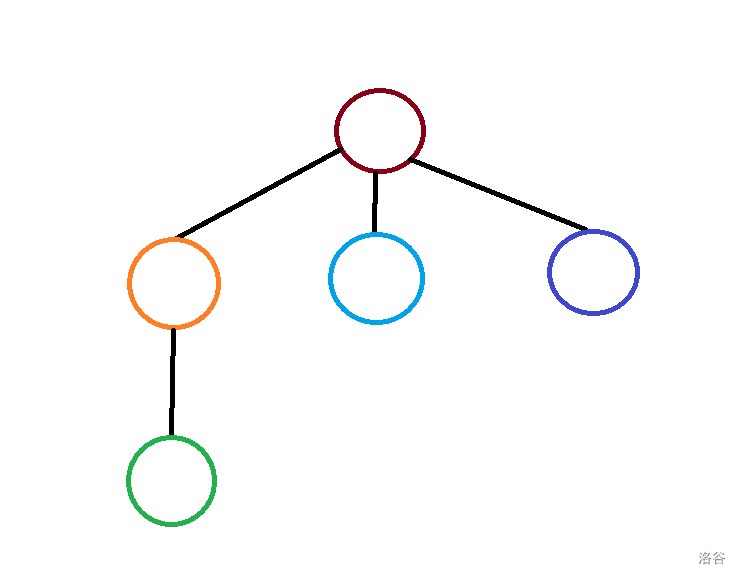
颜色与不同重链一一对应。由于重链剖分必定会把每个点到根节点切成不超过 log⁡n\log n 条链，所以这棵树的树高最多是 log⁡n\log n。
在树剖求 LCA 中，我们反复把两个节点往上跳，直到跳到同一条重链上。在我们把重链缩成一个点的图中，也就是跳到两个点所在重链的 LCA 上。树剖 LCA 对于这棵树的跳法显然是暴力跳，因为一次只跳一条重链，也就是图中的一条边。但是树高只有 log⁡n\log n，所以时间复杂度还是 O(log⁡n)O(\log n) 的。
可不可以更快的求出这个 LCA？由于树剖最多会剖出 O(n)O(n) 条链，所以这个树是 O(n)O(n) 个节点，O(log⁡n)O(\log n) 深度的一棵树。
我们回顾之前的 LCA 算法。为了表述简洁，用 dd 来表示树的高度。
  • 欧拉序，dfs 序 LCA。这两种 LCA 因为需要预处理长度为 O(n)O(n) 的 ST 表，所以树的深度对这两种方法的复杂度没有影响，ST 表必须要有 log⁡n\log n 层。于是用这种算法求 LCA 会在重链很多的时候复杂度被卡退化，比如一棵深度为 22 的树，所有叶子节点都指向同一个根，这样就会有 n−1n-1 条重链。
  • 树剖求 LCA。树剖剖出来的跳到根节点所需的链不是 O(log⁡d)O(\log d) 的，而是 O(log⁡n)O(\log n) 的，想象一棵完全二叉树，必定有一个节点到根节点的路径全都是轻边。于是这种做法也会被卡退化（你可以画一个完全三叉树试一试，两次树剖，把重链缩成一个点之后树的高度还是不变）。
  • 倍增求 LCA。正解出场！倍增每个节点的倍增数组的意义是“从这个节点往上跳 2i2^i 步会到达的节点”，所以树很浅的时候，自然可以开少一点倍增数组。比如高度为 log⁡n\log n 的时候，对于每个节点我们只需要开 log⁡log⁡n\log\log n 长度的倍增数组，求 LCA 的时候也只需要从 log⁡log⁡n\log\log n 层往下枚举。所以倍增 LCA 其实是空间复杂度 O(nlog⁡d)O(n\log d)，求 LCA O(log⁡d)O(\log d) 的。
于是，我们可以对这一棵把重链缩成一个点的树倍增求 LCA。由于树的高度是 log⁡n\log n，所以倍增预处理 O(nlog⁡log⁡n)O(n\log \log n)，求 LCA O(log⁡log⁡n)O(\log\log n)。

代码

写了一点注释，应该还是比较好理解的。
代码 11CPP
#include<bits/stdc++.h>
using namespace std;
const int N = 5e5 + 10;
int n, m, s, top[N][6] , dep[N], ldep[N], fa[N], siz[N], son[N], rtop[N];
vector<int> vt[N];
void dfs1(int x) {//重剖 
	siz[x] = 1;
	dep[x] = dep[fa[x]] + 1;//节点的真实深度，判定LCA那个是更浅的节点 
	for(int i = 0; i < vt[x].size(); i++) {
		if(vt[x][i] != fa[x]) {
			fa[vt[x][i]] = x;
			dfs1(vt[x][i]);
			siz[x] += siz[vt[x][i]];
			if(siz[vt[x][i]] > siz[son[x]]) son[x] = vt[x][i];
		}
	}
}
void dfs2(int x, int tp) {
	ldep[x] = ldep[fa[tp]] + 1;//链深，到根节点需要跳的链数 
	top[x][0] = fa[tp];//下一条链 
	rtop[x] = tp;
	if(son[x]) dfs2(son[x], tp);
	for(int i = 0; i < vt[x].size(); i++) {
		if(vt[x][i] != fa[x] && vt[x][i] != son[x]) dfs2(vt[x][i], vt[x][i]);
	}
}
void init_lca() {
	//log log n在n<=2^32的时候都<=5。所以5够了。 
	for(int i = 1; i <= 5; i++) {
		for(int j = 1; j <= n; j++) {
			top[j][i] = top[top[j][i - 1]][i - 1];
		}
	}
}
int lca(int u, int v) {
	if(ldep[u] < ldep[v]) swap(u, v);//让u成为链深更深的节点 
	for(int i = 5; i >= 0; i--) {//让u,v同一链深
		if(ldep[u] - (1 << i) >= ldep[v]) {
			u = top[u][i];
		}
	}
	if(rtop[u] == rtop[v]) return dep[u] < dep[v] ? u : v;
	for(int i = 5; i >= 0; i--) {//跳到链顶相同 
		if(rtop[top[u][i]] != rtop[top[v][i]]) {
			u = top[u][i]; v = top[v][i];
		}
	}
	u = top[u][0];
	v = top[v][0];
	return dep[u] < dep[v] ? u : v; 
}
int main() {
	ios :: sync_with_stdio(0);
	cin.tie(0); cout.tie(0);
	cin >> n >> m >> s;
	for(int i = 1; i <= n - 1; i++) {
		int u, v;
		cin >> u >> v;
		vt[u].push_back(v);
		vt[v].push_back(u);
	}
	dfs1(s);
	dfs2(s, s);
	init_lca();
	for(int i = 1; i <= m; i++) {
		int a, b;
		cin >> a >> b;
		cout << lca(a, b) << endl;
	}
	return 0;
}
下面这个代码有调试输入输出，可以帮理解执行过程：
代码2CPP
#include<bits/stdc++.h>
using namespace std;
const int N = 5e5 + 10;
const int debug = 0;//调试开关，0为关， 1为开 
int n, m, s, top[N][6] , dep[N], ldep[N], fa[N], siz[N], son[N], rtop[N];
vector<int> vt[N];
void dfs1(int x) {//重剖 
	siz[x] = 1;
	dep[x] = dep[fa[x]] + 1;//节点的真实深度，判定LCA那个是更浅的节点 
	for(int i = 0; i < vt[x].size(); i++) {
		if(vt[x][i] != fa[x]) {
			fa[vt[x][i]] = x;
			dfs1(vt[x][i]);
			siz[x] += siz[vt[x][i]];
			if(siz[vt[x][i]] > siz[son[x]]) son[x] = vt[x][i];
		}
	}
}
void dfs2(int x, int tp) {
	ldep[x] = ldep[fa[tp]] + 1;//链深，到根节点需要跳的链数 
	top[x][0] = fa[tp];//下一条链 
	rtop[x] = tp;
	if(son[x]) dfs2(son[x], tp);
	for(int i = 0; i < vt[x].size(); i++) {
		if(vt[x][i] != fa[x] && vt[x][i] != son[x]) dfs2(vt[x][i], vt[x][i]);
	}
}
void init_lca() {
	//log log n在n<=2^32的时候都<=5。所以5够了。 
	for(int i = 1; i <= 5; i++) {
		for(int j = 1; j <= n; j++) {
			top[j][i] = top[top[j][i - 1]][i - 1];
		}
	}
}
int lca(int u, int v) {
	if(debug == 1) cout << u << " " << v << " " << ldep[u] << " " << ldep[v] << endl;
	if(ldep[u] < ldep[v]) swap(u, v);//让u成为链深更深的节点 
	for(int i = 5; i >= 0; i--) {//让u,v同一链深
		if(ldep[u] - (1 << i) >= ldep[v]) {
			u = top[u][i];
			if(debug == 1) cout << "adjust u:" << u << endl;
		}
	}
	if(rtop[u] == rtop[v]) return dep[u] < dep[v] ? u : v;
	for(int i = 5; i >= 0; i--) {//跳到链顶相同 
		if(rtop[top[u][i]] != rtop[top[v][i]]) {
			if(debug == 1) cout << "jump:" << "u=" << u << ",v=" << v << endl;
			u = top[u][i]; v = top[v][i];
		}
	}
	u = top[u][0];
	v = top[v][0];
	return dep[u] < dep[v] ? u : v; 
}
void print() {
	cout << "fa:"; for(int i = 1; i <= n; i++) cout << fa[i] << " "; cout << endl;
	cout << "siz:"; for(int i = 1; i <= n; i++) cout << siz[i] << " "; cout << endl;
	cout << "dep:"; for(int i = 1; i <= n; i++) cout << dep[i] << " "; cout << endl;
	cout << "ldep:"; for(int i = 1; i <= n; i++) cout << ldep[i] << " "; cout << endl;
	cout << "son:"; for(int i = 1; i <= n; i++) cout << son[i] << " "; cout << endl; 
	cout << "top:\n"; 
	for(int i = 0; i <= 1; i++) {for(int j = 1; j <= 5; j++) cout << top[j][i] << " ";  cout << endl;}
}
int main() {
	ios :: sync_with_stdio(0);
	cin.tie(0); cout.tie(0);
	cin >> n >> m >> s;
	for(int i = 1; i <= n - 1; i++) {
		int u, v;
		cin >> u >> v;
		vt[u].push_back(v);
		vt[v].push_back(u);
	}
	dfs1(s);
	dfs2(s, s);
	init_lca();
    if(debug == 1) print();
	for(int i = 1; i <= m; i++) {
		int a, b;
		cin >> a >> b;
		cout << lca(a, b) << endl;
	}
	return 0;
}
但是令人疑惑的是为什么第二份代码跑的比第一份代码快。

总结

我们实现了一个O(nlog⁡log⁡n)O(n\log\log n) 预处理，O(log⁡log⁡n)O(\log\log n) 求 LCA 的代码（虽然常数有点大只能勉强跑过树剖）。
这份代码的理论时间复杂度仅劣于四毛子这种神奇的算法，而且常数小得多，好写的多。希望我的研究（其实是写完树剖 LCA 之后突然想出来的东西）对大家有帮助。

评论

共 18 条评论，欢迎与作者交流。

正在加载评论...