专栏文章

题解：P9061 [Ynoi2002] Optimal Ordered Problem Solver

PPizzaYY
P9061题解参与者 2已保存评论 1

文章操作

快速查看文章及其快照的属性，并进行相关操作。

当前评论
1 条
当前快照
1 份
快照标识符
@min5vkf5
此快照首次捕获于
2025/12/01 21:04
3 个月前
此快照最后确认于
2025/12/01 21:04
3 个月前
查看原文

思路

首先发现，被操作过的点一定会形成一段轮廓线，且随着 x 坐标的增加，y 坐标单调不升。如下图所示。
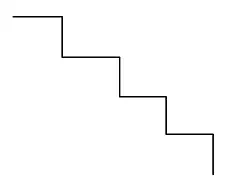
还剩下一些散点在轮廓线之外，我们把这两部分分开做。
首先对于轮廓线上的点，使用 FHQ-Treap 维护每个点的坐标 (x,y)(x,y)。修改操作一定是修改一段区间，把这段区间分裂出来，打上对 x 坐标或者 y 坐标覆盖标记。
然后修改的时候会有一些点加入轮廓线，显然每个点最多加入一次，所以直接将这些点修改后的坐标插入平衡树即可。
查询的时候轮廓线上的点也是一段区间，把这段区间求出来即可。
对于轮廓线外的点，设第 ii 个点第一次被修改到轮廓线上的时间为 tit_i，这个东西类似于二维偏序，离线扫描线即可。
那么对当前第 kk 次操作之后有贡献当且仅当 ti>k,xi≤Xi,yi≤Yit_i>k,x_i\le X_i,y_i\le Y_i，这是一个三维偏序的形式，可以离线做 CDQ 分治。复杂度为 O(nlog⁡2n)O(n\log^2 n)。
然而这显然不够优秀，考虑优化。
首先查询的点在轮廓线的下方答案就是 00，可以忽略。
否则考虑计算不合法的个数，这个相当于 ti>k,xi>Xi,yi≥Yit_i>k,x_i>X_i,y_i\ge Y_i 并上 ti>k,xi≥Xi,yi>Yit_i>k,x_i\ge X_i,y_i>Y_i 的个数。
使用容斥拆分为 ti>k,xi>Xit_i>k,x_i>X_i 的个数加上 ti>k,yi>Yit_i>k,y_i>Y_i 的个数减去 ti>k,xi>Xi,yi>Yit_i>k,x_i>X_i,y_i>Y_i 的个数。由于在满足 xi>Xi,yi>Yix_i>X_i,y_i>Y_i 时一定满足 ti>kt_i>k，所以就是三个二维数点，也可以用离线扫描线解决。
时间复杂度 O(nlog⁡n)O(n\log n)，但是得注意常数。

卡常

这可是 Ynoi 的题还能不卡常？
首先一定要使用快读。
扫描线中，不能使用 vector 存储挂在当前扫到的数下的点，正确的做法是把所有点存到一个数组里然后排序，扫描线中使用双指针求这些点。
每一次修改会插入一些点，若每次都分裂一次再合并，也是不优的。更优秀的做法是先全部分裂开，然后插入这些点后再合并。不过这一点不是特别需要。
查询时不能将这个区间分裂出来然后输出这颗树的大小，然后把分裂出来的树合并。正确的做法是不分裂，直接求。
具体的，由于 xx 小的是一段前缀，yy 小的是一段后缀，现在要求交集的大小，可以单独求出这个前缀和后缀，然后容斥求出答案。

代码

CPP
#include<bits/stdc++.h>
using namespace std;
namespace IO{
    const int BUF=1<<22;
    char buff[BUF],*p1=buff,*p2=buff;
    #define gc() (p1==p2&&(p2=((p1=buff)+fread(buff,1,BUF,stdin)),p1==p2)?EOF:*p1++)
    template<typename T>inline void read(T &x){
        char ch=gc();x=0;int f=1;
        while(!isdigit(ch)){if(ch=='-')f=-1;ch=gc();}
        while(isdigit(ch)) x=(x<<1)+(x<<3)+(ch^48),ch=gc();
        x*=f;
    }
    char obuf[BUF],*p3=obuf;
    inline void pc(char ch){
        if(p3-obuf<BUF) *p3++=ch;
        else fwrite(obuf,p3-obuf,1,stdout),p3=obuf,*p3++=ch;
    }
    inline void put(const char *s){while(*s) pc(*s),++s;}
    char ch[32];int ctop;
    template<typename T>inline void write(T x){
    	if(x<0) x=~x+1,pc('-');
        if(!x) return pc(48);
        while(x) ch[++ctop]=x%10^48,x/=10;
        while(ctop) pc(ch[ctop--]);
    }
    inline void flush(){fwrite(obuf,p3-obuf,1,stdout);p3=obuf;}
}
using namespace IO;
const int N = 1e6+5;
int n,m;
mt19937 rnd(1145141);
struct node{
	int x,y,sz,ls,rs,key,tagx,tagy;
}t[N];
int rt,x,y,z,cnt;
int make(int x,int y)
{
	++cnt;
	t[cnt].sz = 1;
	t[cnt].tagx = t[cnt].tagy = -1;
	t[cnt].x = x,t[cnt].y = y;
	t[cnt].key = rnd();
	return cnt;
}
inline void pushup(int k){t[k].sz = t[t[k].ls].sz+t[t[k].rs].sz+1;}
inline void coverx(int k,int v){t[k].tagx = t[k].x = v;}
inline void covery(int k,int v){t[k].tagy = t[k].y = v;}
inline void down(int k)
{
	if(t[k].tagx!=-1)
	{
		if(t[k].ls) coverx(t[k].ls,t[k].tagx);
		if(t[k].rs) coverx(t[k].rs,t[k].tagx);
		t[k].tagx = -1;
	}
	if(t[k].tagy!=-1)
	{
		if(t[k].ls) covery(t[k].ls,t[k].tagy);
		if(t[k].rs) covery(t[k].rs,t[k].tagy);
		t[k].tagy = -1;
	}
}
int merge(int x,int y)
{
	if(!x||!y) return x+y;
	if(t[x].key<t[y].key)
	{
		down(x),t[x].rs = merge(t[x].rs,y),pushup(x);
		return x;
	}
	else
	{
		down(y),t[y].ls = merge(x,t[y].ls),pushup(y);
		return y;
	} 
}
void splitx(int k,int v,int &x,int &y)
{
	if(!k) return x = y = 0,void();
	down(k);
	if(t[k].x<=v) x = k,splitx(t[k].rs,v,t[k].rs,y);
	else y = k,splitx(t[k].ls,v,x,t[k].ls);
	pushup(k);
}
void splity(int k,int v,int &x,int &y)
{
	if(!k) return x = y = 0,void();
	down(k);
	if(t[k].y>=v) x = k,splity(t[k].rs,v,t[k].rs,y);
	else y = k,splity(t[k].ls,v,x,t[k].ls);
	pushup(k);
}
void split(int k,int v1,int v2,int &x,int &y)
{
	if(!k) return x = y = 0,void();
	down(k);
	if(t[k].x<v1||(t[k].x==v1&&t[k].y>v2)) x = k,split(t[k].rs,v1,v2,t[k].rs,y);
	else y = k,split(t[k].ls,v1,v2,x,t[k].ls);
	pushup(k);
}
int askx(int k,int v)
{
	if(!k) return 0;
	down(k);
	if(t[k].x<=v) return t[t[k].ls].sz+1+askx(t[k].rs,v);
	else return askx(t[k].ls,v);
}
int asky(int k,int v)
{
	if(!k) return 0;
	down(k);
	if(t[k].y<=v) return t[t[k].rs].sz+1+asky(t[k].ls,v);
	else return asky(t[k].rs,v);
}
#define lowbit(x) (x&(-x)) 
namespace t1{
	int t[N];
	inline void add(int x,int v)
	{
		for(;x&&t[x]>v;x-=lowbit(x))
			t[x] = v;
	}
	inline int ask(int x)
	{
		int res = m+1;
		for(;x<=n;x+=lowbit(x))
			res = min(res,t[x]);
		return res;
	}
}
namespace t2{
	int t[N];
	inline void add(int x,int v)
	{
		for(;x;x-=lowbit(x))
			t[x]+=v;
	}
	inline int ask(int x)
	{
		int res = 0;
		for(;x<=n;x+=lowbit(x))
			res+=t[x];
		return res;
	}
}
int O[N],A[N],B[N],X[N],Y[N];
struct node1{
	int w,x;
	inline friend bool operator < (node1 x,node1 y)
	{
		return x.w<y.w;
	}
}vec2[N],vec3[N],vec4[N];
int cnt2,cnt3,cnt4;
struct node2{
	int w,x,y;
	inline friend bool operator < (node2 x,node2 y)
	{
		return x.w<y.w;
	}
}vec1[N];
int cnt1;
bool ok[N];
int ans[N];
int p[N];
pair<int,int> now[N];
inline bool cmp(pair<int,int> x,pair<int,int> y){return (x.first==y.first)?(x.second>y.second):(x.first<y.first);}
signed main()
{
	read(n),read(m);
	for(int i = 1,x,y;i<=n;i++)
		read(x),read(y),vec2[++cnt2] = {x,y};
	for(int i = 1;i<=m;i++)
	{
		read(O[i]),read(A[i]),read(B[i]),read(X[i]),read(Y[i]);
		vec3[++cnt3] = {A[i],i},vec4[++cnt4] = {X[i],i};
	}
	sort(vec2+1,vec2+cnt2+1);
	sort(vec3+1,vec3+cnt3+1);
	sort(vec4+1,vec4+cnt4+1);
	for(int i = 1;i<=n;i++) t1::t[i] = m+1;
	int p2 = cnt2,p3 = cnt3,p4 = cnt4;
	for(int i = n;i;i--)
	{
		while(p3&&vec3[p3].w>=i)
		{
			int j = vec3[p3].x;
			t1::add(B[j],j);
			p3--;
		}
		while(p2&&vec2[p2].w>=i)
		{
			int j = vec2[p2].x;
			vec1[++cnt1] = {t1::ask(j),i,j};
			p2--;
		}
		while(p4&&vec4[p4].w>=i-1)
		{
			int j = vec4[p4].x;
			if(j>=t1::ask(Y[j]+1)) ok[j] = 1;
			p4--;
		}
	}
	sort(vec1+1,vec1+cnt1+1);
	int p1 = cnt1;
	for(int i = m;i;i--)
	{
		while(p1&&vec1[p1].w>=i+1) t2::add(vec1[p1].x,1),p1--;
		ans[i]+=t2::ask(X[i]+1);
	}
	for(int i = 1;i<=n;i++) t2::t[i] = 0;
	p1 = cnt1;
	for(int i = m;i;i--)
	{
		while(p1&&vec1[p1].w>=i+1) t2::add(vec1[p1].y,1),p1--;
		ans[i]+=t2::ask(Y[i]+1);
	}
	for(int i = 1;i<=n;i++) t2::t[i] = 0;
	p2 = cnt2,p4 = cnt4;
	for(int i = n;i;i--)
	{
		while(p2&&vec2[p2].w>=i+1)
		{
			int j = vec2[p2].x;
			t2::add(j,1);
			p2--;
		}
		while(p4&&vec4[p4].w>=i)
		{
			int j = vec4[p4].x;
			ans[j]-=t2::ask(Y[j]+1);
			p4--;
		}
	}
	int tmp = 0;
	p1 = 1;
	for(int i = 1;i<=m;i++)
	{
		splitx(rt,A[i],x,z);
		splity(x,B[i]+1,x,y);
		if(y)
		{
			if(O[i]==2) coverx(y,A[i]);
			else covery(y,B[i]);
		}
		rt = merge(x,merge(y,z));
		int tot = 0; 
		while(p1<=cnt1&&vec1[p1].w<=i)
		{
			tmp++;
			int X = vec1[p1].x,Y = vec1[p1].y;
			if(O[i]==2) X = A[i];
			else Y = B[i];
			now[++tot] = {X,Y};
			p1++;
		}
		sort(now+1,now+tot+1,cmp);
		p[0] = rt;
		for(int i = 1;i<=tot;i++)
		{
			split(p[i-1],now[i].first,now[i].second,p[i-1],p[i]);
			p[i-1] = merge(p[i-1],make(now[i].first,now[i].second));
		}
		rt = 0;
		for(int i = 0;i<=tot;i++)
			rt = merge(rt,p[i]);
		if(!ok[i]) ans[i] = n-tmp-ans[i]+max(askx(rt,X[i])+asky(rt,Y[i])-tmp,0);
	}
	for(int i = 1;i<=m;i++)
	{
		if(ok[i]) ans[i] = 0;
		write(ans[i]),pc('\n'); 
	}
	flush();
	return 0;
}

评论

共 1 条评论，欢迎与作者交流。

正在加载评论...