如何运用人类力量暴力破解 2025 浙江中考数学 T24

省流：我是唐龙，力大无穷。抛弃大脑，暴力求导。

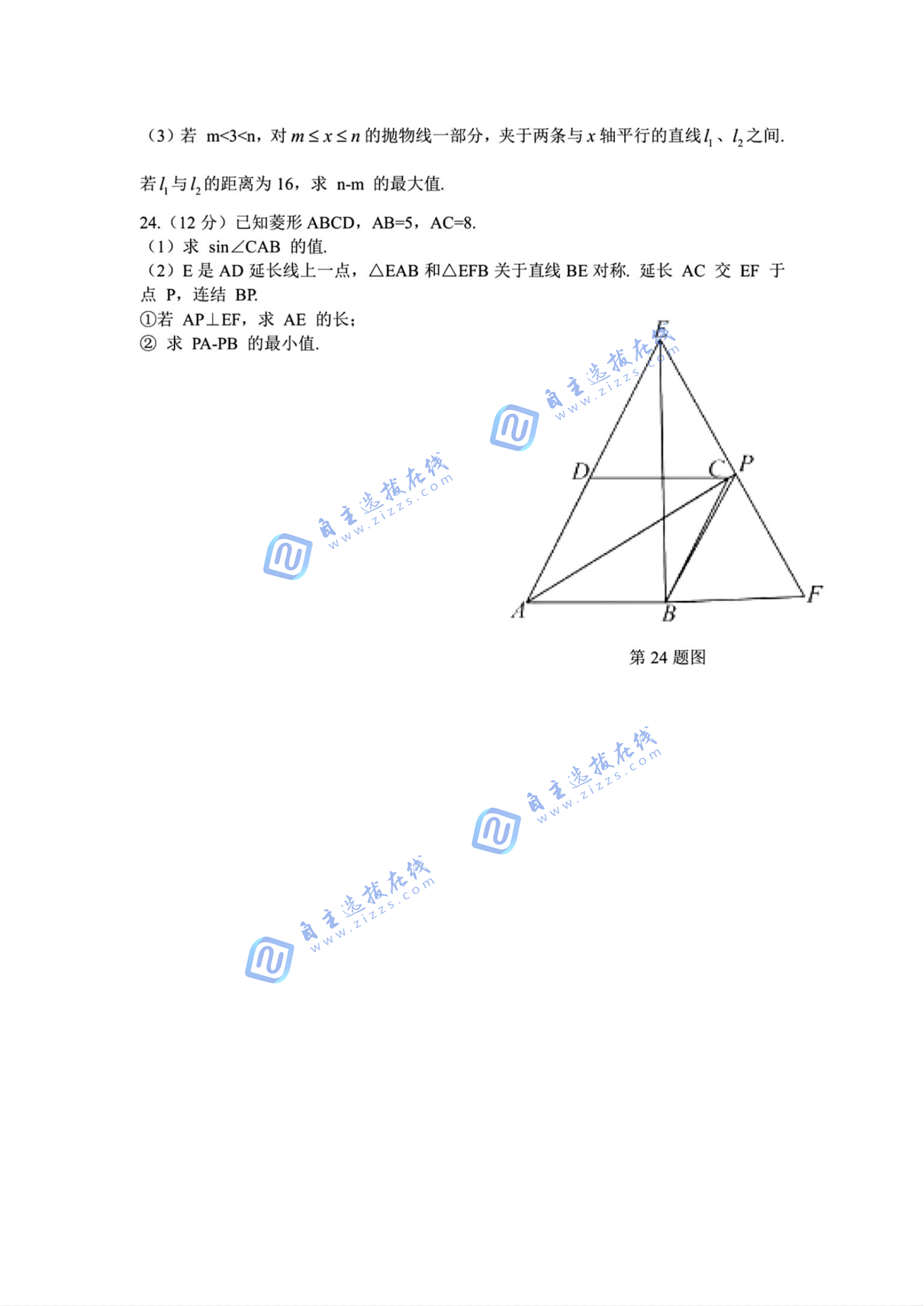
直接看最后一问。$P$ 在 $\text{AC}$ 延长线的情况是容易的。答案为 $3$。仅考虑 $P$ 在 $\text{AC}$ 上的情况。

令 $\angle \text{CAB}=\theta,\text{AP}=x$。则 $\text{PC}=8-x$。在 $\triangle\text{PCB}$ 中运用余弦定理得到 $\text{PB}=\sqrt{x^2-8x+25}$。那么 $\text{PA}-\text{PB}=x-\sqrt{x^2-8x+25}$。

令 $f(x)=x-\sqrt{x^2-8x+25}$，求导得到 $f'(x)=1-\dfrac{x-4}{\sqrt{x^2-8x+25}}$。注意到：

所以 $f'(x)>0$ 恒成立。即 $f(x)$ 在 $\mathbb{R}$ 上单调递增。只需求出 $x$ 的最小值。

接下来令 $\angle\text{AEB}=\varphi$。可以通过构造外角来证明 $\varphi$ 随着 $\text{DE}$ 变长而减小。且 $\text{DE}$ 趋近于正无穷的时候 $\varphi$ 趋近于 $0$。因此 $\varphi\in\left(0,\dfrac{\pi}{2}-\theta\right)$。

在 $\triangle\text{ABE}$ 中，由正弦定理：

解得 $\text{AE}=\dfrac{5\sin(2\theta+\varphi)}{\sin\varphi}$。在 $\triangle\text{AEP}$ 中由正弦定理：

运用和角公式和二倍角公式整理后可得 $x=\dfrac{24+24\cos2\varphi+7\sin2\varphi}{4\sin2\varphi+3\cos2\varphi}$。

令 $t=2\varphi$，则 $t\in(0,\pi-2\theta)$。令 $g(t)=\dfrac{24+24\cos t+7\sin t}{4\sin t+3\cos t}$。考虑求解 $g(t)$ 的单调区间，令 $g'(t)>0$，整理后可得 $24\sin t-32\cos t>25$。运用辅助角公式得到 $\sin(t-\alpha)>\dfrac{5}{8}$，其中 $\alpha\in\left(0,\dfrac{\pi}{2}\right)$，且 $\sin\alpha=\dfrac{4}{5},\cos\alpha=\dfrac{3}{5}$。可以发现 $\theta+\alpha=\dfrac{\pi}{2}$。所以 $t-\alpha\in(-\alpha,\alpha)\sube\left(-\dfrac{\pi}{2},\dfrac{\pi}{2}\right)$。

再令 $\beta\in\left(0,\dfrac{\pi}{2}\right)$，且 $\sin\beta=\dfrac{5}{8},\cos\beta=\dfrac{\sqrt{39}}{8}$。由于 $\sin\beta<\dfrac{4}{5}=\sin\alpha$。结合正弦函数在 $\left(-\dfrac{\pi}{2},\dfrac{\pi}{2}\right)$ 上的单调性可得 $\beta<\alpha$。所以 $\beta\in(-\alpha,\alpha)$。同时 $\sin(t-\alpha)$ 在 $(0,\pi-2\theta)$ 上单调递增。且当 $t=\alpha+\beta$ 时 $\sin(t-\alpha)=\dfrac{5}{8}$。因此 $g(t)$ 的单调递减区间为 $(0,\alpha+\beta)$，单调递增区间为 $(\alpha+\beta,\pi-2\theta)$。因此最小值在 $t=\alpha+\beta$ 时取到。将其代入原函数。注意 $\sin\beta>\sin\theta$，结合单调性可以知道 $\beta>\theta$。因此 $\alpha+\beta>\dfrac{\pi}{2}$，余弦值应当取负值。有：

可以计算出此时 $g(t)=4+\dfrac{3\sqrt{39}}{5}$。因此 $\text{AP}$ 的最小值为 $4+\dfrac{3\sqrt{39}}{5}$。将其代入 $f(x)$ 可以得到答案为 $\dfrac{3\sqrt{39}-4}{5}$。

做完了。没有任何难度。去年考这个我不赢麻了？