专栏文章

树上启发式合并

ssuperkkkeee
算法·理论参与者 1已保存评论 0

文章操作

快速查看文章及其快照的属性，并进行相关操作。

当前评论
0 条
当前快照
1 份
快照标识符
@minjw7mt
此快照首次捕获于
2025/12/02 03:37
3 个月前
此快照最后确认于
2025/12/02 03:37
3 个月前
查看原文

树上启发式合并

这次更新了一些例题
题单

问题导入

CF600E

题意

给点一个 nn 个点有颜色的的树，
定义 重要地位 为：以 vv 为子树的树出现次数最多的颜色
有 mm 次询问，求以 vv 为子树的所有的 重要地位的编号之和
1≤n≤1051 \le n \le 10^5

思路

如果直接暴力会 O(N2)O(N^2)
所以我们要考虑一种新方法：
树上启发式合并
树上启发式合并一般是解决一类不带修的子树查询问题
其本质为利用重链剖分的性质优化子树贡献的计算
我们会先跑轻儿子，然后把贡献累加到重儿子身上，在通过重儿子，具体操作如下：
  1. 若该点为轻儿子，则算该轻儿子的 ansans，然后清空该儿子 cntcnt 的贡献
  2. 若该点为重儿子，则算该重儿子的 ansans，但是不用清空 cntcnt 贡献
  3. 再枚举轻儿子，加入轻儿子的贡献就得到了xx 的答案
Q：为什么不会 cntcnt 算重
A：应为轻儿子的 cntcnt 都清空了，在步骤 33 中跳过了重儿子，所以不会算重
代码如下：
CPP
#include<bits/stdc++.h>
using namespace std;
#define int long long
int n;
vector<int> p[100001];
int siz[100001];
int son[100001];
int cnt[100001];
int col[100001];
int ans[100001];
int maxx;
int sum;
void df(int x,int fa) //求出重儿子
{
	siz[x]=1;
	for(int xx:p[x])
	{
		if(xx==fa) continue;
		df(xx,x);
		siz[x]+=siz[xx];
		if(siz[xx]>siz[son[x]]||son[x]==0) son[x]=xx;
	}
}
void add(int x,int fa,int son) //加入贡献并统计答案
{
	cnt[col[x]]++;
	if(cnt[col[x]]>maxx) 
	{
		maxx=cnt[col[x]];
		sum=col[x];
	}
	else if(cnt[col[x]]==maxx)
	{
		sum+=col[x];
	}
	for(int xx:p[x])
	{
		if(xx==fa||xx==son) continue;
		add(xx,x,son);
	}
}
void del(int x,int fa) //删除轻儿子的贡献
{
	cnt[col[x]]--;
	for(int xx:p[x]) 
	{
		if(xx==fa) continue;
		del(xx,x);
	}
}
void ds(int x,int fa,bool flag)
{
	for(int xx:p[x])
	{
		if(xx==fa||xx==son[x]) continue;
		ds(xx,x,0);
	} //先枚举轻儿子并统计答案
	if(son[x]) ds(son[x],x,1); //再枚举重儿子
	add(x,fa,son[x]); //统计答案
	ans[x]=sum;
	if(!flag) //删除轻儿子的贡献
	{
		del(x,fa);
		sum=0;
		maxx=0;
	}
}
对于每一个询问，我们直接输出 ansvans_v 即可
最终代码如下：
CPP
#include<bits/stdc++.h>
using namespace std;
#define int long long
int n;
vector<int> p[100001];
int siz[100001];
int son[100001];
int cnt[100001];
int col[100001];
int ans[100001];
int maxx;
int sum;
void df(int x,int fa)
{
	siz[x]=1;
	for(int xx:p[x])
	{
		if(xx==fa) continue;
		df(xx,x);
		siz[x]+=siz[xx];
		if(siz[xx]>siz[son[x]]||son[x]==0) son[x]=xx;
	}
}
void add(int x,int fa,int son)
{
	cnt[col[x]]++;
	if(cnt[col[x]]>maxx) 
	{
		maxx=cnt[col[x]];
		sum=col[x];
	}
	else if(cnt[col[x]]==maxx)
	{
		sum+=col[x];
	}
	for(int xx:p[x])
	{
		if(xx==fa||xx==son) continue;
		add(xx,x,son);
	}
}
void del(int x,int fa)  
{
	cnt[col[x]]--;
	for(int xx:p[x]) 
	{
		if(xx==fa) continue;
		del(xx,x);
	}
}
void ds(int x,int fa,bool flag)
{
	for(int xx:p[x])
	{
		if(xx==fa||xx==son[x]) continue;
		ds(xx,x,0);
	}
	if(son[x]) ds(son[x],x,1);
	add(x,fa,son[x]);
	ans[x]=sum;
	if(!flag)
	{
		del(x,fa);
		sum=0;
		maxx=0;
	}
}
signed main()
{
	ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
	cin>>n;
	for(int i=1;i<=n;i++) cin>>col[i];
	for(int i=1;i<n;i++)
	{
		int u,v; cin>>u>>v;
		p[u].push_back(v);
		p[v].push_back(u);
	}
	df(1,0);
	ds(1,0,0);
	for(int i=1;i<=n;i++) cout<<ans[i]<<" ";
	return 0;
}

习题1

U41492

题意

给点一个 nn 个点有颜色的的树，求所有子树出现的颜色数目

思路

与第一题相同，可以用树上启发式合并，统计答案就修改即可
代码：
CPP
#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,m;
vector<int> p[100001];
int siz[100001];
int son[100001];
int cnt[100001];
int col[100001];
int ans[100001];
int maxx;
int sum;
void df(int x,int fa)
{
	siz[x]=1;
	for(int xx:p[x])
	{
		if(xx==fa) continue;
		df(xx,x);
		siz[x]+=siz[xx];
		if(siz[xx]>siz[son[x]]||son[x]==0) son[x]=xx;
	}
}
void add(int x,int fa,int son)
{
	cnt[col[x]]++;
	if(cnt[col[x]]==1) sum++;
	for(int xx:p[x])
	{
		if(xx==fa||xx==son) continue;
		add(xx,x,son);
	}
}
void del(int x,int fa)
{
	cnt[col[x]]--;
	for(int xx:p[x]) 
	{
		if(xx==fa) continue;
		del(xx,x);
	}
}
void ds(int x,int fa,bool flag)
{
	for(int xx:p[x])
	{
		if(xx==fa||xx==son[x]) continue;
		ds(xx,x,0);
	}
	if(son[x]) ds(son[x],x,1);
	add(x,fa,son[x]);
	ans[x]=sum;
	if(!flag)
	{
		del(x,fa);
		sum=0;
		maxx=0;
	}
}
signed main()
{
	ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
	cin>>n;
	for(int i=1;i<n;i++)
	{
		int u,v; cin>>u>>v;
		p[u].push_back(v);
		p[v].push_back(u);
	}
	for(int i=1;i<=n;i++) cin>>col[i];
	df(1,0);
	ds(1,0,0);
	cin>>m;
	while(m--)
	{
		int x; cin>>x;
		cout<<ans[x]<<'\n';
	}
	return 0;
}

习题2

CF1709E

闲话

感觉这题应该评紫

题面

给定一颗有 nn 个点的树，点有点权 aia_i
每次操作可以修改一个点权，求最少多少次修改可以使不存在任意一条路径上点权的异或和为 00
1≤n≤2×105,1≤ai≤2301 \le n \le 2 \times 10^5,1 \le a_i \le 2^{30}

思路

我们可以先对这棵树做一个前缀和sumisum_i，为 11 到 ii 的点权异或和
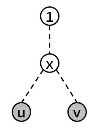
如果有一条非法路径（u→vu \to v，xx为 u,vu,v的 lcalca），即au⊗⋯⊗ax⊗⋯⊗av=0a_u \otimes \cdots \otimes a_x \otimes \cdots \otimes a_v = 0
用 sumsum 表示则为
sumu⊗sumv⊗ax=0sum_u \otimes sum_v \otimes a_x = 0
sumu=sumv⊗axsum_u = sum_v \otimes a_x
若我们向修改点权使得这条式子不成立，我们自然就把 axa_x 改一下，我们可以把 axa_x 改成一个大于 2302^{30} 的数，这样就可以使任何 ai⊗axa_i \otimes a_x  /=\mathrlap{\,/}{=} 00
改完以后，我们就可以把 xx 看为一个断点，xx 的祖先都无法通过 xx 这条路找到非法路径，那我们就把 xx 的子树集合清空，不用算贡献了
对于维护，我们可以使用树上启发式合并，
对于每个点，我们都单开一个 setset 储存 xx 子树的 sumsum
对于一个节点 xx 的子树
  • 如果没有发现非法路径，则将儿子 yy 的 setyset_y 合并到 setxset_x （启发式合并）
  • 若发现了，则将 ans+1ans + 1，并且将 setxset_x 清空
寻找非法路径也很简单：
根据上面的柿子 sumu=sumv⊗axsum_u = sum_v \otimes a_x
我们只要在枚举的 setyset_y 中枚举 sumvsum_v 再在 setxset_x 中寻找 sumv⊗axsum_v \otimes a_x，如果找到了，就说明存在一条非法路径 u→x→vu \to x \to v
代码如下:
CPP
#include<bits/stdc++.h>
using namespace std;
int n;
int a[200001];
int sum[200001];
vector<int> p[200001];
set<int> s[200001];
int ans;
void dfs(int x,int fa)
{
	s[x].insert(sum[x]);
	bool flag=0;
	for(int xx:p[x])
	{
		if(xx==fa) continue;
		sum[xx]=sum[x]^a[xx];
		dfs(xx,x);
		if(s[x].size()<s[xx].size()) swap(s[x],s[xx]);
		for(int xxx:s[xx])
		{
			if(s[x].find(xxx^a[x])!=s[x].end()) 
			{
				flag=1; break;
			}
		}
		for(int xxx:s[xx]) s[x].insert(xxx);
	}
	if(flag)
	{
		ans++; set<int>().swap(s[x]);
	}
}
signed main()
{
	ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
	cin>>n;
	for(int i=1;i<=n;i++) cin>>a[i];
	for(int i=1;i<n;i++)
	{
		int u,v; cin>>u>>v;
		p[u].push_back(v);
		p[v].push_back(u);
	}
	dfs(1,0);
	cout<<ans;
	return 0;
}
加上 setset 的总时间复杂度为 O(nlog⁡2n)O(n \log^2n)，但实际跑不满

习题3

CF208E

题面

有一颗以 00 为根的树。
有 mm 次询问，求 xx 与多少个点拥有相同的 的 kk 级祖先
1≤n,m≤1051 \le n,m \le 10^5

思路

暴力显然是不现实的，我们需要做一下转化
首先，我们可以通过倍增求出 xx 的 2k2^k 级祖先，设 xx 的 kk 级祖先为 yy
转化：本题可以转化为 yy 有多少个 kk 级儿子
我们自然要对询问做改变：
我们可以把 xx 的询问挂在 yy 上离线统计贡献，可该如何统计呢？
我们不妨设 cnticnt_i 为以 xx 为子树中，深度为的 ii 的点有多少个
显然我们更新时要用到 树上启发式合并
我们来复习一下其过程
  1. 先枚举轻儿子，统计答案，但清空 cntcnt 的贡献
  2. 枚举重儿子，统计答案，cntcnt 直接继承到当前节点
  3. 枚举轻儿子，统计 cntcnt
添加和删除可以写一个函数，引入一个参数 zz，直接把 cntdepx+zcnt_{dep_x}+z 即可
当我们跑到一个挂有查询的节点是，当前节点的答案就为 cntdepx+k−1cnt_{dep_x+k}-1
因为离线，所以最后结果输出 ansians_i 就可以了
Q：如何求 xx 的 kk 级祖先？
A：现将 kk 二进制分解，从最低为开始（第 00 位），若该位 ii为 11，则将当前的 xx 往上跳 2i2^i 级，最后的 xx 就是 xx 的 kk 级祖先
时间复杂度应为 O(nlog⁡n)O(n \log n)
代码如下：
CPP
#include<bits/stdc++.h>
using namespace std;
int n,m;
vector<int> p[100001];
int dep[100001];
int son[100001];
int siz[100001];
int bz[100001][21];
int cnt[100001];
int ans[100001];
struct node
{
	int x,id;
};
vector<node> pp[100001];
void df(int x,int fa)
{
	dep[x]=dep[fa]+1;
	siz[x]=1;
	bz[x][0]=fa;
	for(int i=1;i<=20;i++) bz[x][i]=bz[bz[x][i-1]][i-1];
	for(int xx:p[x])
	{
		if(xx==fa) continue;
		df(xx,x);
		siz[x]+=siz[xx];
		if(siz[son[x]]<siz[xx]||son[x]==-1) son[x]=xx;
	}
}
void add(int x,int fa,int k)
{
	cnt[dep[x]]+=k;
	for(int xx:p[x])
	{
		if(xx==fa) continue;
		add(xx,x,k);
	}
}
void ds(int x,int fa,bool flag)
{
	for(int xx:p[x])
	{
		if(xx==fa||xx==son[x]) continue;
		ds(xx,x,1);
	}
	if(son[x]!=-1) ds(son[x],x,0);
	cnt[dep[x]]++;
	for(int xx:p[x])
	{
		if(xx==fa||xx==son[x]) continue;
		add(xx,x,1);
	}
	for(node xx:pp[x]) ans[xx.id]=cnt[dep[x]+xx.x]-1;
	if(flag) add(x,fa,-1);
}
signed main()
{	
	ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		int x; cin>>x;
		p[x].push_back(i);
		son[i]=-1;
	}
	son[0]=-1;
	df(0,0);
	cin>>m;
	for(int q=1;q<=m;q++)
	{
		int x,k; cin>>x>>k;
		int fa=x;
		for(int i=0;(1<<i)<=k;i++)
		{
			if(((1<<i)&k)==(1<<i)) fa=bz[fa][i];
		}
		if(fa==0) ans[q]=0;
		else pp[fa].push_back({k,q});
	}
	ds(0,0,0);
	for(int i=1;i<=m;i++) cout<<ans[i]<<" ";
	return 0;
}

习题4

CF570D

题面

有一颗 nn 个节点的树，每个节点有一个字母
有 mm 次询问，每次询问求以 xx 为根的子树中，（全局）深度为 yy 的节点上的数字是否可以组成回文数
1≤n,m≤5000001 \le n,m \le 500000，字母均为小写英文字母

思路

我们先对题目做一下转化:
对于回文，我们知道回文数是由 00 或 11 个奇数次出现字符和若干个偶数次出现字符组成
也就是说，只要我当前的字符集里又出现超过 11 次的奇数，那么这个数肯定不是回文数，反之则是
转化为 cntcnt，即 cnticnt_i %\% 2==12 == 1 的 ii 数量不能超过 11
那么我们的问题就转化为求 cntcnt 数组
因为询问是按照深度分层，所以我们的 cntcnt 数组应该是二维的，第一维是深度，第二维是字母
那我们的问题就转化为静态无修改树求 cntcnt，不难想象到用树上启发式合并
步骤和习题3 差不多，add 的操作也一样
那我们就展示代码
CPP
#include<bits/stdc++.h>
using namespace std;
int n,m;
vector<int> p[500001];
int a[500001];
int cnt[500001][31];
int dep[500001];
int siz[500001];
int son[500001];
int ans[500001];
struct node
{
	int x,id;
};
vector<node> pp[500001];
void df(int x,int fa)
{
	dep[x]=dep[fa]+1;
	siz[x]=0;
	for(int xx:p[x])
	{
		if(xx==fa) continue;
		df(xx,x);
		siz[x]+=siz[xx];
		if(siz[son[x]]<siz[xx]||son[x]==0) son[x]=xx;
	}
}
void add(int x,int fa,int k)
{
	cnt[dep[x]][a[x]]+=k;
	for(int xx:p[x])
	{
		if(xx==fa) continue;
		add(xx,x,k);
	}
	
}
void ds(int x,int fa,bool flag)
{
	for(int xx:p[x])
	{
		if(xx==fa||xx==son[x]) continue;
		ds(xx,x,1);
	}
	if(son[x]) ds(son[x],x,0);
	cnt[dep[x]][a[x]]++;
	for(int xx:p[x])
	{
		if(xx==fa||xx==son[x]) continue;
		add(xx,x,1);
	}
	for(node xx:pp[x])
	{
		int f=xx.x;
		int id=xx.id;
		bool q=1;
		int c=0;
		for(int i=0;i<26;i++)
		{
			//cout<<"Qqqqqqqq "<<f<<" "<<i<<" "<<cnt[f][i]<<endl;
			if(cnt[f][i]%2==1) c++;
			if(c>1) 
			{
				q=0; break;
			}
		}
		ans[id]=q;
	}
	if(flag) add(x,fa,-1);
}
signed main()
{	
	ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
	cin>>n>>m;
	for(int i=2;i<=n;i++)
	{
		int x; cin>>x;
		p[x].push_back(i);
	}
	for(int i=1;i<=n;i++)
	{
		char x; cin>>x;
		a[i]=x-'a';
	}
	df(1,0);
	for(int i=1;i<=m;i++)
	{
		int x,y; cin>>x>>y;
		if(dep[x]>y) 
		{
			ans[i]=1; continue;
		}
		if(dep[x]==y)
		{
			ans[i]=1; continue;
		}
		pp[x].push_back({y,i});
	}
	ds(1,0,0);
	for(int i=1;i<=m;i++)
	{
		if(ans[i]) cout<<"Yes";
		else cout<<"No";
		cout<<'\n';
	}
	return 0;
}
/*

6 1
1 1 1 3 3
zacccd
3 3

5 1
1 1 2 3
cbcab
1 3

*/

习题5

CF375D

题面

有一颗 nn 个点带颜色的树，有 mm 次询问
每次询问求以 xx 的子树中有多少个颜色出现的次数大于等于 kk
2≤n≤1052 \le n \le 10^5，1≤m≤1051 \le m \le 10^5
颜色 cic_i 不超过 10510^5

思路

注意到 ci≤105c_i \le 10^5，那我们可以设一个 fif_i 为出现 ii 次的颜色数。
设最大颜色为 tt
这个 ff 数组可以在处理颜色数 cntcnt，时同时完成
统计答案就是求 ∑i=ktfi\displaystyle\sum_{i=k}^{t} f_i
但每一次查询时间复杂度是 O(t)O(t)
我们可以使用线段树来维护？
但每一次修改时 O(log⁡n)O(\log n)，总时间复杂的就为 O(nlog⁡2n)O(n \log^2n)，再加上一些常数，有点极限
（下面是正解）
那我们可以重新定义 ff，定义 cntticntt_i 为大于等于 ii 的颜色数
修改 cnttcntt 时就可以像莫队一样修改
维护 cntcnt 可以用树上启发式合并，在节点上挂查询
答案 ansians_i 就是 cnttkicntt_{k_i}
树上启发式合并的复杂的是 O(nlog⁡n)O(n \log n)，查询是 O(1)O(1) 的，总时间复杂的就是 O(nlog⁡n)O(n \log n)
代码：
CPP
#include<bits/stdc++.h>
using namespace std;
int n,m;
int c[100001];
vector<int> p[100001];
int siz[100001];
int son[100001];
struct node
{
	int x,id;
};
vector<node> pp[100001];
int cnt[100001];
int cntt[100001];
int ans[100001];
void df(int x,int fa)
{
	siz[x]=1;
	for(int xx:p[x])
	{
		if(xx==fa) continue;
		df(xx,x);
		siz[x]+=siz[xx];
		if(siz[son[x]]<siz[xx]||son[x]==0) son[x]=xx;
	}
}
void add(int x,int k)
{
	if(k==1)
	{
		cnt[c[x]]++;
		cntt[cnt[c[x]]]++;
	}
	else
	{
		cntt[cnt[c[x]]]--;
		cnt[c[x]]--;
	}
}
void addd(int x,int fa,int k)
{
	add(x,k);
	for(int xx:p[x])
	{
		if(xx==fa) continue;
		addd(xx,x,k);
	}
}
void ds(int x,int fa,bool flag)
{
	for(int xx:p[x])
	{
		if(xx==fa||xx==son[x]) continue;
		ds(xx,x,1);
	}
	if(son[x]) ds(son[x],x,0);
	add(x,1);
	for(int xx:p[x])
	{
		if(xx==fa||xx==son[x]) continue;
		addd(xx,x,1);
	}
	for(node xx:pp[x])
	{
		int k=xx.x;
		int id=xx.id;
		ans[id]=cntt[k];
	}
	if(flag) addd(x,fa,-1);
}
signed main()
{	
	ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
	cin>>n>>m;
	for(int i=1;i<=n;i++) cin>>c[i];
	for(int i=1;i<n;i++)
	{
		int u,v; cin>>u>>v;
		p[u].push_back(v);
		p[v].push_back(u);
	}
	for(int i=1;i<=m;i++)
	{
		int x,k; cin>>x>>k;
		pp[x].push_back({k,i});
	}
	df(1,0);
	ds(1,0,0);
	for(int i=1;i<=m;i++) cout<<ans[i]<<'\n';
	return 0;
}

习题6

CF246E

题面

给点一颗 nn 个点的森林，用超级源点 00 链接，每个点有名字（名字可能相同），有 mm 次询问
每次询问求 xx 的 kk 级后代有多少个不同的名字
1≤n,m≤1051 \le n,m \le 10^5

思路

这道题不难想到树上启发式合并，但如何维护贡献是个问题
如果把 cnti,jcnt_{i,j} 定义为 ii 的点名字 jj 出现的次数，那么时间和空间都会爆炸
我们可以换一个思路，如果我们把出现的名字都加入一个数组里，然后去重，剩下的数量就是答案了
想到这里，我们可以用 set 来维护
设 ss为一个set， setxset_x 为深度为 xx 的点中出现的名字（已去重）
我们把询问挂在节点上，每次询问的答案就是 setx+kset_{x+k} 的size()
注意：
x+kx+k 可能会大于 nn 所以要开 22 倍数组或判断
如果以 00 为根，那么最大的深度是 n+1n+1，判断时要判断 x+k≤n+1x+k \le n+1，而不是 nn
那么代码：
CPP
#include<bits/stdc++.h>
using namespace std;
int n,m;
vector<int> p[200001];
int dep[200001];
int siz[200001];
int son[200001];
string c[200001];
set<string> s[200001];
struct node
{
	int x,id;
};
vector<node> pp[200001];
int ans[200001];
void df(int x,int fa)
{
	siz[x]=1;
	dep[x]=dep[fa]+1;
	for(int xx:p[x])
	{
		if(xx==fa) continue;
		df(xx,x);
		siz[x]+=siz[xx];
		if(siz[son[x]]<siz[xx]||son[x]==-1) son[x]=xx;
	}
}
void add(int x,int fa)
{
	s[dep[x]].insert(c[x]);
	for(int xx:p[x])
	{
		if(xx==fa) continue;
		add(xx,x);
	}
}
void del(int x,int fa)
{
	//set<string>().swap(s[dep[x]]);
	s[dep[x]].clear();
	for(int xx:p[x])
	{
		if(xx==fa) continue;
		del(xx,x);
	}
}
void ds(int x,int fa,bool flag)
{
	for(int xx:p[x])
	{
		if(xx==fa||xx==son[x]) continue;
		ds(xx,x,1);
	}
	if(son[x]!=-1) ds(son[x],x,0);
	s[dep[x]].insert(c[x]);
	for(int xx:p[x])
	{
		if(x==fa||xx==son[x]) continue;
		add(xx,x);
	}
	for(node xx:pp[x])
	{
		int k=xx.x;
		int id=xx.id;
		//if(dep[x]+k>n+1) continue;
		ans[id]=s[dep[x]+k].size();
	}
	if(flag) del(x,fa);
}
signed main()
{	
	ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		int x; cin>>c[i]>>x;
		p[x].push_back(i);
	}
	for(int i=0;i<=n;i++) son[i]=-1;
	df(0,0);
	cin>>m;
	for(int i=1;i<=m;i++)
	{
		int x,k; cin>>x>>k;
		pp[x].push_back({k,i});
	}
	ds(0,0,0);
	for(int i=1;i<=m;i++) cout<<ans[i]<<'\n';
	return 0;
}

习题7

CF741D
本题较精彩，请耐心观看

题面

有一颗 nn 个点的树，边有一个字母
定义“好”的路径为：路径上的字母通过排列可以组成回文数
求以 xx 为根的子树中，最长的“好”的路径最长是多少。x∈[1,n]x \in [1,n]
1≤n≤5×1051 \le n \le 5 \times 10^5，字母范围从 aa 到 vv

思路

根据回文的性质，回文数最多只会有一个字母出现奇数次
那么一个数是否是回文数就只关心字母出现次数的奇偶
我们对于每一颗子树都开一个 cnt 数组记录每一个字母出现次数，但时间复杂度不能接受
注意到奇偶数的性质：奇数+奇数=偶数+偶数=偶数，奇数+偶数=奇数
这个性质是不是似曾相识呢？
没错，就是异或！
我们设偶数为 00，奇数为 11，那么合并两个数 x,yx,y，就是 x⊗yx \otimes y
注意到字母范围很小，那我们对于每一颗子树做一个类似状压做法
如果要快速求路径 u→vu \to v 的奇偶性？
我们可以先定义一个数组 disxdis_x ，为 1→x1 \to x 的奇偶，那么 disxdis_x 的递推式就是：
disx=disfa⊗wdis_x=dis_{fa} \otimes w
那么 u→vu \to v 的路径就是
disu,v=disu⊗dislca⊗disv⊗dislcadis_{u,v}=dis_u \otimes dis_{lca} \otimes dis_v \otimes dis_{lca}
disu,v=disu⊗disvdis_{u,v}=dis_u \otimes dis_v
如果 u→vu \to v 的路径可以组成回文数，那 disu,vdis_{u,v} 当且仅当等于 00 或 2x2^x
那么对于节点 uu，合法的 vv 的 disvdis_v 只能是 disudis_u 或 disu⊗2xdis_u \otimes 2^x
那我们找合法的 vv 就只用枚举 2x2^x 就可以了
对于合法路径 u→vu \to v，其它对 lcalca 的贡献就是 depu+depv−2×deplcadep_u + dep_v - 2 \times dep_{lca}
那我们求最大贡献肯定要是 depudep_u 和 depvdep_v 最大
那我们就可以记录奇偶性为 disxdis_x 的节点最大的深度为 cntdisxcnt_{dis_x}
设 lcalca 为 xx 吧
那 xx 的贡献就是：
  1. 若以 xx 为端点，则贡献为 cntdisx−depxcnt_{dis_x}-dep_x
  2. 若路径经过 xx，则加上递归取max
  3. 若路径不经过 xx，即路径在 xx 的某个子树内，则贡献就为子树的最大贡献
那 xx 的最大贡献就是以上的最大值
第 22 中情况的代码如下：
CPP
void add(int x,int fa,int k)
{
	if(cnt[dis[x]])
	{
		ans[k]=max(ans[k],cnt[dis[x]]+dep[x]-2*dep[k]);
	}
	for(int i=0;i<=21;i++)
	{
		if(cnt[dis[x]^(1<<i)])
		{
			ans[k]=max(ans[k],cnt[dis[x]^(1<<i)]+dep[x]-2*dep[k]);	
		}
	}
	for(node xx:p[x])
	{
		int v=xx.v;
		if(v==fa) continue;
		add(v,x,k);
	}
}
若直接统计 cntcnt 是 O(n2)\Omicron (n^2) 的
那统计 cntcnt 就可以使用树上启发式合并，时间复杂度是 O(nlog⁡n)\Omicron(n \log n)
代码：
CPP
#include<bits/stdc++.h>
using namespace std;
int n;
struct node
{
	int v,w;
};
vector<node> p[2000001];
int dis[2000001];
int siz[2000001];
int dep[2000001];
int son[2000001];
int cnt[20000001];
int ans[2000001];
void df(int x,int fa)
{
	siz[x]=1;
	dep[x]=dep[fa]+1;
	for(node xx:p[x])
	{
		int v=xx.v;
		int w=xx.w;
		if(v==fa) continue;
		dis[v]=dis[x]^w;
		df(v,x);
		siz[x]+=siz[v];
		if(siz[son[x]]<siz[v]||son[x]==0) son[x]=v;
	}
}
void add(int x,int fa,int k)
{
	if(cnt[dis[x]])
	{
		ans[k]=max(ans[k],cnt[dis[x]]+dep[x]-2*dep[k]);
	}
	for(int i=0;i<=21;i++)
		{
			if(cnt[dis[x]^(1<<i)])
			{
				ans[k]=max(ans[k],cnt[dis[x]^(1<<i)]+dep[x]-2*dep[k]);	
			}
		}
	for(node xx:p[x])
	{
		int v=xx.v;
		if(v==fa) continue;
		add(v,x,k);
	}
}
void del(int x,int fa)
{
	cnt[dis[x]]=0;
	for(node xx:p[x])
	{
		int v=xx.v;
		if(v==fa) continue;
		del(v,x);
	}
}
void addd(int x,int fa)
{
	cnt[dis[x]]=max(cnt[dis[x]],dep[x]);
	for(node xx:p[x])
	{
		int v=xx.v;
		if(v==fa) continue;
		addd(v,x);
	}
}
void ds(int x,int fa,bool flag)
{
	for(node xx:p[x])
	{
		int v=xx.v;
		if(v==fa||v==son[x]) continue;
		ds(v,x,1);
		ans[x]=max(ans[x],ans[v]);
	}
	if(son[x])
	{
		ds(son[x],x,0);
		ans[x]=max(ans[x],ans[son[x]]);
	}
	if(cnt[dis[x]]) ans[x]=max(ans[x],cnt[dis[x]]-dep[x]);
	for(int i=0;i<=21;i++)
	{
		if(cnt[dis[x]^(1<<i)])
		{
			ans[x]=max(ans[x],cnt[dis[x]^(1<<i)]-dep[x]);
		}
	}
	cnt[dis[x]]=max(cnt[dis[x]],dep[x]);
	for(node xx:p[x])
	{
		int v=xx.v;
		if(v==fa||v==son[x]) continue;
		add(v,x,x);
		addd(v,x);
	}
	if(flag) del(x,fa);
}
signed main()
{	
	ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
	cin>>n;
	for(int i=2;i<=n;i++)
	{
		int x;
		char ox; cin>>x>>ox;
		int w=ox-'a';
		p[x].push_back({i,(1ll<<w)});
	}
	df(1,0);
	ds(1,0,0);
	for(int i=1;i<=n;i++) cout<<ans[i]<<" ";
	return 0;
}

总结

本题的转化十分巧妙，将字母出现的奇偶性转化为二进制，并且使用异或来合并
在统计贡献是也要想全面，不能漏情况
总的来说这题是一道十分巧妙的好题，适合读者思考研究

评论

共 0 条评论，欢迎与作者交流。

正在加载评论...