Solution of AT_tenka1_2018_e Equilateral

Consider drawing the Huffman distance of three points.

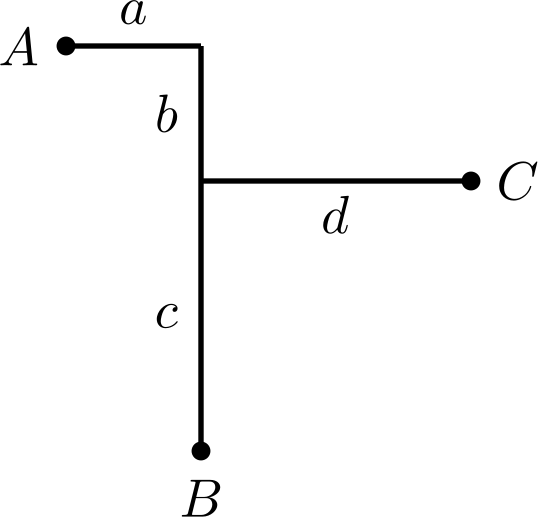
Then we have $a+b+c=a+b+d=c+d$, i.e. $a+b=c=d$. This means that the slope of $\overline{BC}$ is $\pm1$ and $A$ is on a line parallel to it.

We might as well $\mathcal{O}(n^2)$ enumerate $B$, $\mathcal{O}(n)$ enumerate $C$, and compute the number of legal $A$ by difference $\mathcal{O}(1)$. Complexity $\mathcal{O}(n^3)$ with large constants.

Specifically, we enumerate $(i,j)$ and $k<i$, and the problem translates into finding the number of $a_{x,y}=1$ on the four lines. It is sufficient to preprocess the prefix sum for each line with slope $\pm1$.

Note that to avoid double counting , it may be worthwhile to count the special endpoint positions separately.