专栏文章
P14302 基础倍增练习题 6 - 斜二进制倍增
P14302题解参与者 4已保存评论 3
文章操作
快速查看文章及其快照的属性,并进行相关操作。
- 当前评论
- 3 条
- 当前快照
- 1 份
- 快照标识符
- @minhttd1
- 此快照首次捕获于
- 2025/12/02 02:39 3 个月前
- 此快照最后确认于
- 2025/12/02 02:39 3 个月前
参考:斜二进制倍增。
Update:10.31 更改了之前表述不严谨的地方。
斜二进制倍增
斜二进制倍增,应用在树上问题,可以做到:
- 在线 加叶子;
- 单次 查询树链信息,信息不需要可差分(但需要满足结合律);
- 单点修改;
- 空间复杂度是小常数 。
原理
像树状数组一样,每个点记录包含自己的一段前缀信息。同时每个点也开一个数组记录自己的信息。
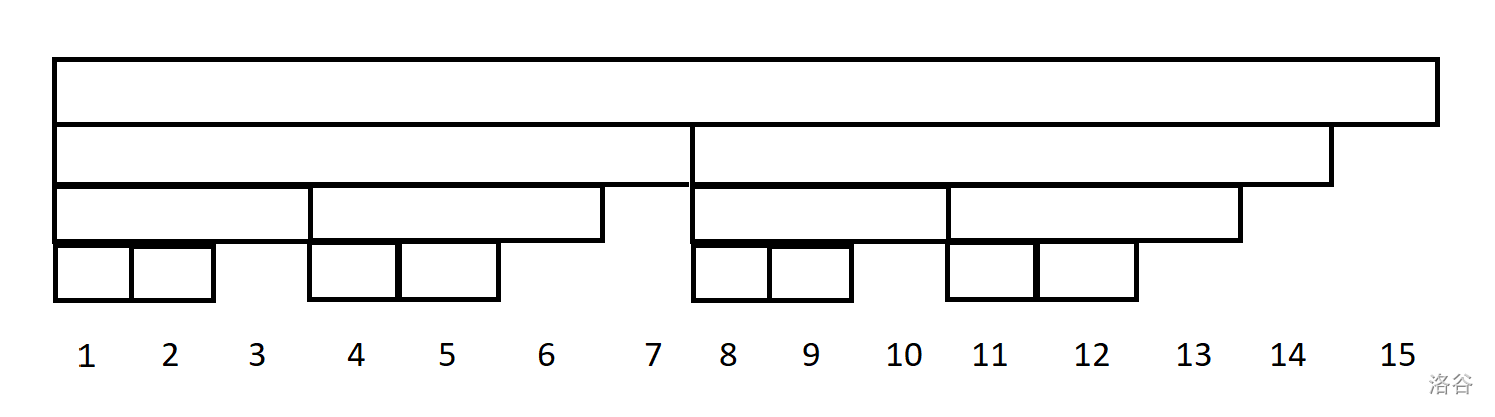
设 管辖的范围 。 管辖的范围:
- 如果 管辖的区间与 长度相同,那么 就管辖 管辖的、 管辖的,以及自己的信息;
- 这里称 管辖的区间是 管辖的、 管辖的区间的上一级区间;
- 否则 就只管辖自己的信息。
声明一些数组:
- 表示 。 是 管辖的区间左端点。这个数组帮助我们在查询时,跳到上一个与当前区间紧挨着的区间;
- 表示 的上一级区间中恰好包含 的区间的管辖点。这个数组帮助我们跳到上一级父亲;
- 表示某个点管辖区间的信息;
- 表示某个点自己的信息。
实现
单点修改:往 跳,不断修改当前点的信息。
区间查询:往 跳。若当前点 管辖区间完全包含询问区间,那么用 更新,并跳到 。否则用 更新,并跳到 。
后缀加点:实现定义即可。
- 如果 管辖的区间与 长度相同,那么 就管辖 管辖的、 管辖的,以及自己的信息;
- 否则 就只管辖自己的信息。
时间复杂度
这里主要讲区间查询的复杂度。
考虑第一次满足 管辖区间不完全包含询问区间的时刻 。
在时刻 之前,每次跳跃要么往同级区间跳,要么往上一级区间跳。且跳 次同级区间就会往上一级区间跳。
在时刻 及之后,每次跳跃要么往同级区间跳,要么往下一级区间跳。且跳 次同级区间就会往下一级区间跳。
两部分时间复杂度都是 ,故单次查询的时间复杂度为 。
树上问题
可以很好迁移。具体的,用每个点的深度(根结点深度为 )来之前区间问题中的下标 。每个点相当于维护从祖先到自己这一条树链的信息。
发现某两条树链的信息若有交,那么交的这一部分信息可以共用。
实现时将区间问题的 换作树上问题的 即可。
树上 LCA
两个点中,深度大的点先跳到和深度小的点同级的位置,然后再两个点同时向上跳跃。
树链信息
深度较浅的点跳到 LCA 的深度,深度较深的点跳到 LCA 深度加 的深度。将两部分拼起来即可。
题解
题目:P14302 基础倍增练习题 6。
一开始 个带点权的孤立点。每次操作要么是连边,要么查询树链点权的最大子段和。 和询问次数 。强制在线。内存 MB。
发现树链剖分不能处理在线连边,ST 表式倍增内存会爆。所以可以用斜二进制倍增。
下面默认 和 同阶。
每次连边时,考虑将 小的那一边的每一个点加到 大的那一边。启发式合并均摊是 的。调用动态加点函数即可。每一次加点是 的,这部分是 的。
每次查询,两边分别往上跳,跳到 LCA 的位置,并把沿途信息记录下来。这一部分也是 。
所以总体是 的。瓶颈在于查询时向上跳时信息合并,这里常数会比较大。
代码
最大子段和部分:
CPPstruct Max_Seq {
LL vl, vr, va, sum;
Max_Seq(LL vl, LL vr, LL va, LL sum):
vl(vl), vr(vr), va(va), sum(sum) {}
Max_Seq() {}
friend Max_Seq operator + (const Max_Seq & a,const Max_Seq & b) {
return Max_Seq(
max(a.vl, a.sum + b.vl),
max(b.vr, b.sum + a.vr),
max({a.va,b.va,a.vr + b.vl}),
a.sum + b.sum
);
}
}tr[N], val[N];
Max_Seq get_rev(Max_Seq x) {
return Max_Seq(x.vr, x.vl, x.va, x.sum);
}
斜二进制的部分:
CPPint fa[N], dth[N], tf[N], lb[N];
void push_up(int x) {
int p = fa[x];
if (p == lb[x]) {
tr[x] = val[x];
} else {
tr[x] = (val[x] + tr[p]) + tr[lb[p]];
}
}
void append(int cu, int pa) {
int p = pa, q = lb[p], r = lb[q];
if (q == 0 || dth[p] - dth[q] != dth[q] - dth[r]) {
lb[cu] = pa;
} else {
tf[p] = tf[q] = cu;
lb[cu] = r;
}
push_up(cu);
}
int get_lca(int x, int y) {
if (dth[x] > dth[y]) {
swap(x, y);
}
while (dth[y] > dth[x]) {
int p = lb[y];
if (dth[p] <= dth[x] - 1) {
y = fa[y];
} else {
y = p;
}
}
while (x != y) {
if (lb[x] != lb[y]) {
x = lb[x], y = lb[y];
} else {
x = fa[x], y = fa[y];
}
}
return x;
}
查询部分:
CPPMax_Seq get_seq(int cu, int d) {
Max_Seq ans = Max_Seq(-inf, 0, -inf, 0);
while (dth[cu] >= d) {
int p = lb[cu];
if (dth[p] < d - 1) {
ans = ans + val[cu];
cu = fa[cu];
} else {
ans = ans + tr[cu];
cu = p;
}
}
return ans;
}
LL query(int x, int y) {
int lca = get_lca(x, y);
if (x == y) return val[x].va;
if (dth[x] > dth[y]) swap(x, y);
Max_Seq p1 = get_seq(x, dth[lca]);
Max_Seq p2 = get_seq(y, dth[lca] + 1);
return (p1 + get_rev(p2)).va;
}
连边部分:(其中
CPPB 是并查集结构体)void dfs(int cu, int pa) {
dth[cu] = dth[pa] + 1;
fa[cu] = pa; //注意先更新再 append
append(cu, pa);
for (int to: e[cu]) {
if (to == pa) continue;
dfs(to, cu);
}
}
void unite(int x, int y) {
int tx = B.bcj(x), ty = B.bcj(y);
if (B.sz[tx] < B.sz[ty]) swap(tx, ty), swap(x, y);
dfs(y, x);
e[x].pb(y);
e[y].pb(x);
B.merge(x, y);
}
相关推荐
评论
共 3 条评论,欢迎与作者交流。
正在加载评论...