P3374 (树状数组1)

思路

题意要求给出一个数列，实现以下操作：

1.将序列内某一个数加 $k$
2.得到某一个区间的数字和

对于单个操作，我们可以使用差分和前缀和，这样可以实现一个操作

O(1)

，另外一个操作

O(n)

，可是两个操作一起上，时间会变成

O(n^2)

了，显然会炸。

所以说我们需要用一个算法来达到

2

个操作之间的平衡，以

O(n\log_n)

的时间复杂度通过这题。

所以说我们需要一个数据结构，以实现区间查询和单点修改的功能。

现在来思考如何实现。

数据结构：

考虑建立一种数据结构，使其可以实现对区间加和的查询和对单个节点的修改。

有一种思路，我们可以构造一颗二叉树，其叶子结点即为其原来数组的值。

再往上走，每两个子结点所对的父节点即为其加和，这样即可实现查询一个节点就实现区间查询。

此时进行优化，由于父节点和左子节可以推出其右子节点，所以我们可以砍去右子节点，此时空间降为

\log_n

。

对于单点修改，只需要对该节点所联系的节点依次加上（或者减去）一个值即可。

这种数据结构叫做树状数组。

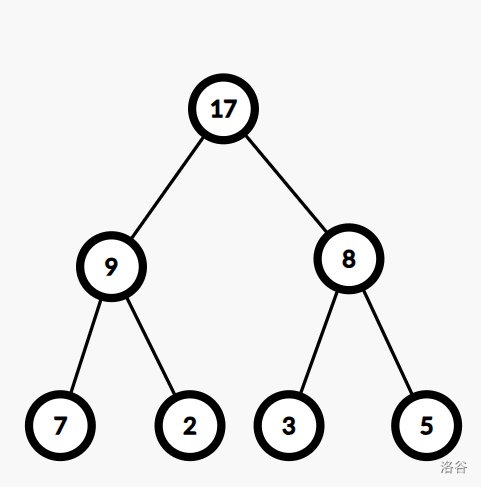
这是一个树状数组的概念图

lowbit

实现树状数组，我们应该思考应该如何查询其节点，lowbit(x) 函数用于获取 ( x ) 的二进制表示中最低位的 1 所对应的值。例如，lowbit(6) 返回 2，因为 6 的二进制是 110，最低位的 1 对应的值是 10（即 2）,借此我们可以表示出每一个节点。

CPP

int lowbit(int x) {
    return x & (-x);

add

对于添加值，我们需要给每一个节点加上这个值，即可视为添加一个节点，从下到上，依次加。

get

对于得到区间和，从上到下，加上每一个值即可。

由于

get(x)

求出的是一到

x

的区间和，所以说这里要用

get(y)-get(x-1)

得到

x

到

y

区间之和。

code:

CPP

#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,m;
int a[8000001];
int c[2000001];
int lowbit(int x){
	return x&(-x);
} 
void add(int x,int k){
	while(x<=n){
		c[x]+=k;
		x+=lowbit(x);
	}
}
int get(int x){
	int ans=0;
	while(x>0){
		ans+=c[x];
		x-=lowbit(x);
	}
	return ans;
}
signed main(){
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		cin>>a[i];	
		add(i,a[i]);	
	}
	for(int i=1;i<=m;i++){
		int opt;
		cin>>opt;
		int x,y;
		cin>>x>>y;
		if(opt==1){
			add(x,y);
		} 
		else{
			if(y<x) swap(x,y);
			cout<<get(y)-get(x-1)<<endl;
		}
	}
    return 0;
}

文章操作

思路