专栏文章

矩阵快速幂入门

mmaichong
算法·理论参与者 20已保存评论 23

文章操作

快速查看文章及其快照的属性，并进行相关操作。

当前评论
23 条
当前快照
1 份
快照标识符
@mkh4lyse
此快照首次捕获于
2026/01/17 01:02
上个月
此快照最后确认于
2026/02/19 01:17
14 小时前
查看原文

参考文章

  1. 矩阵加速：「学习笔记」矩阵快速幂
  2. 图上加速：矩阵类优化 dp——矩阵加速优化

概念

矩阵乘法

设矩阵 C=A×BC=A \times B，则：
  1. 若 AA 是一个 n×pn \times p 的矩阵，BB 是一个 p×mp \times m 的矩阵，则 CC 是一个 n×mn \times m 的矩阵。
  2. C[i][j]C[i][j] 为 A[i][k]×B[k][j]A[i][k] \times B[k][j] 之和（k∈[1,p]k \in [1,p]）。
如图，这是两个 2×22 \times 2 的矩阵相乘的过程：
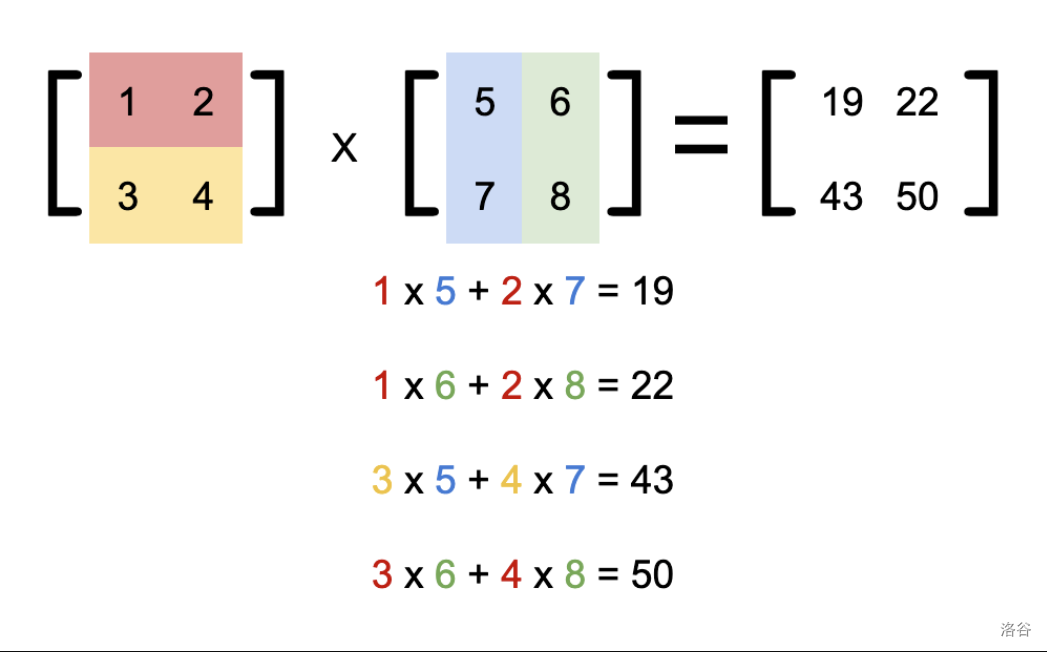
哎呀图怎么挂了
代码CPP
node cheng(node x,node y){//矩阵x和矩阵y相乘 
	node re;//re为两矩阵相乘所得到的结果
	for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)re.a[i][j]=0;//初始化矩阵re 
	for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)for(int k=1;k<=n;k++)re.a[i][j]=(re.a[i][j]+x.a[i][k]*y.a[k][j]%p)%p;
	return re;
}

矩阵快速幂

为了快速求方阵 AnA ^ n，我们可以使用快速幂来优化时间复杂度。

例题：【模板】矩阵快速幂

代码CPP
//这是一份快速求矩阵a的m次方的代码 
#include <bits/stdc++.h>
using namespace std;
const int MAXN=100+10;
long long n,m,p=1e9+7;
struct node{
	long long a[MAXN][MAXN];
}a,ans;
node cheng(node x,node y){//矩阵相乘 
	node re;
	for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)re.a[i][j]=0;
	for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)for(int k=1;k<=n;k++)re.a[i][j]=(re.a[i][j]+x.a[i][k]*y.a[k][j]%p)%p;
	return re;
}
node qpow(node x,long long y){//快速幂 
	if(y==1)return x;
	node tt=qpow(x,y/2);
	node re=cheng(tt,tt);
	if(y%2)re=cheng(re,x);
	return re;
}
int main(){
	cin>>n>>m;
	for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)scanf("%lld",&a.a[i][j]);
	ans=qpow(a,m);
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++)printf("%lld ",ans.a[i][j]);
		printf("\n");
	}
	return 0;
}

应用

矩阵加速

我们可以使用矩阵来加速线性递推式的转移。

例题：斐波那契数列

我们发现，由于 nn 是在 long long 范围以内，所以 O(n)O(n) 的暴力递推肯定不行。
于是，我们考虑用矩阵来加速递推。
设答案矩阵为 A(n)=[f(n)f(n−1)]A(n) = \begin{bmatrix} f(n) & f(n-1) \end{bmatrix}，则 A(n−1)=[f(n−1)f(n−2)]A(n-1) = \begin{bmatrix} f(n-1) & f(n-2) \end{bmatrix}。
现在，我们需要构造一个转移矩阵 VV，使 A(n)=A(n−1)×VA(n)=A(n-1) \times V。
VV 的第一列为 [11]\begin{bmatrix} 1 \\ 1 \end{bmatrix}，因为 f(n)=1×f(n−1)+1×f(n−2)f(n) = 1 \times f(n-1)+1 \times f(n-2)。
V 的第二列为 [10]\begin{bmatrix} 1 \\ 0 \end{bmatrix}，因为 f(n−1)=1×f(n−1)+0×f(n−2)f(n-1) = 1 \times f(n-1)+0 \times f(n-2)。
所以，V=[1110]V = \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix}。
因为 f(2)=1f(2)=1,f(1)=1f(1)=1，所以初始矩阵 A(2)=[11]A(2) = \begin{bmatrix} 1 & 1 \end{bmatrix}。
因为每乘以一遍 VV 就往前推一项，所以我们只需要将 A(2)A(2) 乘上 Vn−2V ^ {n-2} 就可以得到 A(n)A(n) 了。
代码CPP
#include <bits/stdc++.h>
using namespace std;
long long n,p=1e9+7;
struct node{
	long long a[3][3];
}a,v;
node cheng(node x,node y,long long w){//矩阵乘法 
	node re;
	for(int i=1;i<=2;i++)for(int j=1;j<=2;j++)re.a[i][j]=0;
	for(int i=1;i<=w;i++)for(int j=1;j<=2;j++)for(int k=1;k<=2;k++)re.a[i][j]=(re.a[i][j]+x.a[i][k]*y.a[k][j]%p)%p;
	return re;
}
node qpow(node x,long long y){//快速幂 
	if(y==1)return x;
	node tt=qpow(x,y/2);
	node re=cheng(tt,tt,2);
	if(y%2)re=cheng(re,x,2);
	return re;
}
int main(){
	cin>>n;
	if(n<=2){
		cout<<1;
		return 0;
	}
	a.a[1][1]=1,a.a[1][2]=1;//初始化初始矩阵a 
	v.a[1][1]=1,v.a[1][2]=1,v.a[2][1]=1,v.a[2][2]=0;//初始化转移矩阵v 
	cout<<cheng(a,qpow(v,n-2),1).a[1][1]%p;
	return 0;
}

例题：矩阵加速（数列）

设答案矩阵为 A(n)=[f(n)f(n−1)f(n−2)]A(n) = \begin{bmatrix} f(n) & f(n-1) & f(n-2) \end{bmatrix}，所以 A(n−1)=[f(n−1)f(n−2)f(n−3)]A(n-1) = \begin{bmatrix} f(n-1) & f(n-2) & f(n-3) \end{bmatrix}。
经过推导后，我们可以得出转移矩阵 V=[110001100]V = \begin{bmatrix} 1 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \end{bmatrix}。
因为 f(3)=1f(3)=1,f(2)=1f(2)=1,f(1)=1f(1)=1，所以初始矩阵 A(3)=[111]A(3) = \begin{bmatrix} 1 & 1 & 1 \end{bmatrix}，所以 A(n)=A(3)×Vn−3A(n) = A(3) \times V ^ {n-3}。

例题：广义斐波那契数列

设答案矩阵为 A(n)=[f(n)f(n−1)]A(n) = \begin{bmatrix} f(n) & f(n-1) \end{bmatrix}，则 A(n−1)=[f(n−1)f(n−2)]A(n-1) = \begin{bmatrix} f(n-1) & f(n-2) \end{bmatrix}。
转移矩阵 V=[p1q0]V = \begin{bmatrix} p & 1 \\ q & 0 \end{bmatrix}。
初始矩阵 A(2)=[a2a1]A(2)=\begin{bmatrix} a2 & a1 \end{bmatrix}，所以 A(n)=A(2)×Vn−2A(n) = A(2) \times V ^ {n-2}。

例题：[NOI2012] 随机数生成器

设答案矩阵为 A(n)=[Xnc]A(n) = \begin{bmatrix} X_n & c \end{bmatrix}， 则 A(n−1)=[Xn−1c]A(n-1) = \begin{bmatrix} X_{n-1} & c \end{bmatrix}。
经过推导后，我们可以得到转移矩阵 V=[a011]V = \begin{bmatrix} a & 0 \\ 1 & 1 \end{bmatrix}。
初始矩阵 A(0)=[X0c]A(0) = \begin{bmatrix} X_0 & c \end{bmatrix}，所以 A(n)=A(0)×VnA(n) = A(0) \times V ^ n。
注意：由于数据较大，容易爆 long long，本题在做乘法时要使用龟速乘。

图上加速

众所周知，邻接矩阵也是一种矩阵。
联系上文中矩阵乘法的式子和加法原理以及乘法原理，易得出：设 BB 为一个图的邻接矩阵，则在 BkB ^ k 中，B[i][j]B[i][j] 表示节点 ii 经过 kk 步到节点 jj 的方案数。

例题：[TJOI2017] 可乐

对于行为：前往相邻城市，我们可以直接建出图的邻接矩阵 AA，然后在计算出 AkA ^ k 后统计所有的 Ak[1][i]A ^ k [1][i] 之和。
对于行为：停在原地，我们将其看做自环即可。
对于行为：爆炸，我们可以新建一个不存在的节点 00，然后从每个点（包括 00 自己）都向它连一条有向边，到达节点 00 即为爆炸。
代码CPP
#include <bits/stdc++.h>
using namespace std;
const int MAXN=30+10;
int n,m,p=2017,t,ans;
struct node{
	int a[MAXN][MAXN];
}a,v;
node cheng(node x,node y){
	node re;
	for(int i=0;i<=n;i++)for(int j=0;j<=n;j++)re.a[i][j]=0;
	for(int i=0;i<=n;i++)for(int j=0;j<=n;j++)for(int k=0;k<=n;k++)re.a[i][j]=(re.a[i][j]+x.a[i][k]*y.a[k][j])%p;
	return re;
}
node qpow(node x,int y){
	if(y==1)return x;
	node tt=qpow(x,y/2);
	node re=cheng(tt,tt);
	if(y%2)re=cheng(re,x);
	return re;
}
int main(){
	cin>>n>>m;
	for(int i=1;i<=m;i++){
		int x,y;
		scanf("%d%d",&x,&y);
		a.a[x][y]=a.a[y][x]=1;
	}
	for(int i=0;i<=n;i++)a.a[i][0]=1,a.a[i][i]=1;//建爆炸和停在原地的边 
	cin>>t;
	v=qpow(a,t);
	for(int i=0;i<=n;i++)ans=(ans+v.a[1][i])%p;
	cout<<ans;
	return 0;
}

例题：[SCOI2009] 迷路

我们发现，这题与板子的不同之处在于这题有边权，不能直接由邻接矩阵的乘方得出答案。
我们发现边权极小，只在 1−91-9 之间，于是，我们考虑通过拆边或拆点，将本题转化为板子题来做。
先考虑拆边，将一条长为 ww 的边拆为 w−1w-1 个点所组成的链，这样一来，边权就全变为 11 了，就可以直接套版子做了。
但是，我们发现：在拆完边后，最多会出现 10001000 个点，矩阵乘法会 TLE。
于是，我们考虑拆点。设 uu 为图上一点，我们将 uu 拆为 99 个点，每个点分别负责 uu 的一种边权的出边，边权为 11 的出边连在负责边权为 11 的节点上，边权为 22 的出边连在负责边权为 22 的节点上，以此类推。
同时，所有负责边权为 ii 的节点也要向负责边权为 i+1i+1 的节点连边。这样一来，边权再次全部变为了 11，就可以套板子做了：跑一遍新图的邻接矩阵的 tt 次方，记为 ansans。ans[1][n的负责边权为1的节点的编号]ans[1][n的负责边权为1的节点的编号] 即为答案。

评论

共 23 条评论，欢迎与作者交流。

正在加载评论...