字典序最小的最小割

怎么都用跑

n

遍网络流来解决字典序最小的最小割呢？

所以本题解就来介绍（且只介绍）跑完一次网络流后用

O(n+m)

来求出字典序最小的最小割的方法，对于原题的建模转换，可以去看看其他题解。

先跑一次网络流，随后我们在残余网络（即只把有流量的边拿出来建的新图）上跑一遍 Tarjan，会得到一张 DAG，并且这张 DAG 上只有满流边（否则其与其反边都有流量，就会被缩掉）。

考虑最小割在这张 DAG 表现出来什么特征，容易发现一个割集

\{S,T\}

是最小割，当且仅当不存在

T\to S

的满流边，割这种边一定不优。

于是考虑按编号从小到大枚举每条边

(u,v)

来贪心构造

\{S,T\}

，具体的，查看这条边是不是确定了

u\in T

或

v\in S

，如果是，那么它肯定不能存在于最小割中；否则就将其加入最小割，并把

u

的前驱标记为属于

S

，

v

的后继标记为属于

T

。

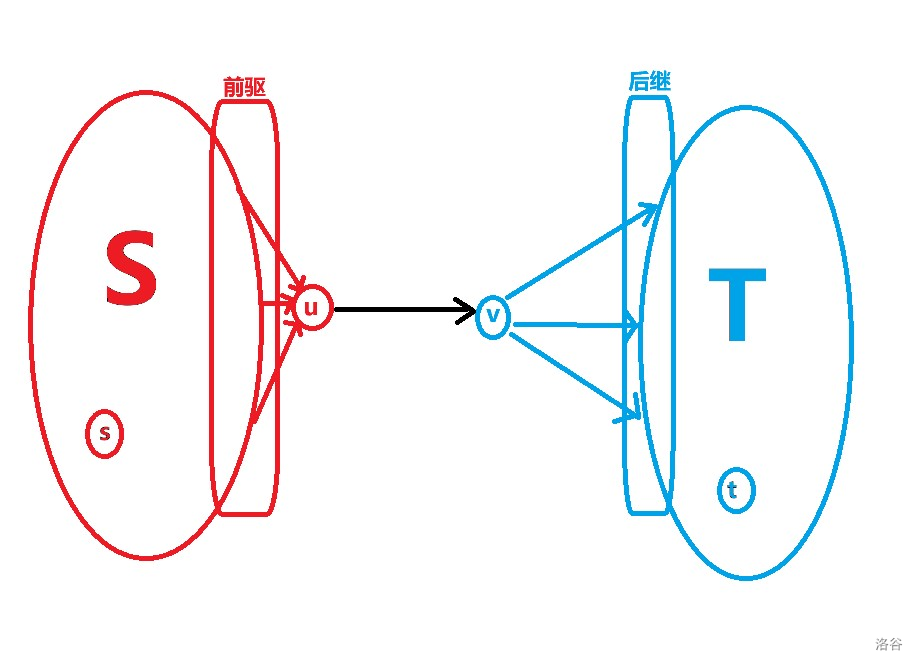
（拙劣的示意图）

因为每个点只会被遍历一次所以这个地方复杂度

O(n+m)

。

CPP

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
const int N=705*2;
int n,a[N],b[N];struct Item{int c,id;bool operator<(const Item&_)const{return c<_.c;}}c[N];
int f[N],S,T,id[N];
struct Edge{int v;ll c;int ne;}e[N*N];int h[N],cur[N],ecnt;
void add(int u,int v,ll c){
    e[++ecnt]={v,c,h[u]};h[u]=cur[u]=ecnt;
    e[++ecnt]={u,0,h[v]};h[v]=cur[v]=ecnt;
}
int gap[N],dis[N];
ll dfs(int u,ll lim){
    if(u==T)return lim;
    int sum=0;
    for(int &i=cur[u];i;i=e[i].ne){
        if(e[i].c&&dis[u]==dis[e[i].v]+1){
            ll res=dfs(e[i].v,min(lim,e[i].c));
            e[i].c-=res;e[i^1].c+=res;sum+=res;lim-=res;
            if(!lim)return sum;
        }
    }
    if(!--gap[dis[u]])dis[S]=T+2;
    gap[++dis[u]]++;
    cur[u]=h[u];
    return sum;
}
ll Dinic(){
    ll ans=0;rep(i,0,T+2)gap[i]=dis[i]=0;
    gap[0]=T+1;
    while(dis[S]<T+2)ans+=dfs(S,1e14);
    return ans;
}
int tim,dfn[N],low[N],sta[N],tp;bool in[N];
int cnt,bel[N];
void dfs2(int x){
    dfn[x]=low[x]=++tim;
    sta[++tp]=x;in[x]=1;
    for(int i=h[x];i;i=e[i].ne){
        if(!e[i].c)continue;
        if(!dfn[e[i].v]){
            dfs2(e[i].v);
            low[x]=min(low[x],low[e[i].v]);
        }else if(in[e[i].v])low[x]=min(low[x],dfn[e[i].v]);
    }
    if(dfn[x]==low[x]){
        cnt++;
        while(in[x]){
            in[sta[tp]]=0;
            bel[sta[tp]]=cnt;tp--;
        }
    }
}
int col[N];
void dfs3(int x,int co){
    if(col[x])return ;
    col[x]=(co?1:-1);
    for(int i=h[x];i;i=e[i].ne){
        if((co?e[i^1].c:e[i].c)||bel[x]==bel[e[i].v])dfs3(e[i].v,co);
    }
}
void solve(){
    scanf("%d",&n);
    rep(i,1,n)scanf("%d",&a[i]);
    rep(i,1,n)scanf("%d",&b[i]);
    rep(i,1,n)scanf("%d",&c[i].c),c[i].id=i;
    f[0]=0;int mx=0;
    rep(i,1,n){
        f[i]=0;
        rep(j,0,i-1)if(a[j]<a[i])f[i]=max(f[i],f[j]+1);
        mx=max(mx,f[i]);
    }
    ecnt=1;S=0;T=2*n+1;
    rep(i,1,n){
        if(f[i]==1)add(S,i*2-1,1e14);
        if(f[i]==mx)add(i*2,T,1e14);
        rep(j,1,i-1)if(f[j]==f[i]-1&&a[j]<a[i])add(j*2,i*2-1,1e14);
        add(i*2-1,i*2,b[i]);id[i]=ecnt-1;
    }
    ll ans=Dinic(),sum=0;
    printf("%lld ",ans);vector<int>tans;
    sort(c+1,c+n+1);
    rep(i,S,T)if(!dfn[i])dfs2(i);
    dfs3(S,0);dfs3(T,1);
    rep(i,1,n){
        if(e[id[c[i].id]].c)continue;
        int u=c[i].id*2-1,v=c[i].id*2;
        if(bel[u]==bel[v])continue;
        //col=1表示归属于T，col=-1表示归属于S
        if(col[u]!=1&&col[v]!=-1)tans.push_back(c[i].id),dfs3(u,0),dfs3(v,1);
    }
    sort(tans.begin(),tans.end());
    printf("%d ",tans.size());puts("");
    for(auto j:tans)printf("%d ",j);puts("");
    rep(i,S,T)h[i]=dfn[i]=low[i]=in[i]=sta[i]=bel[i]=col[i]=0;tp=cnt=tim=0;
}
int main(){
    int T;scanf("%d",&T);
    while(T--)solve();
    return 0;
}

跑得比较快，目前最优解。

字典序最小的最小割

文章操作

相关推荐

评论

字典序最小的最小割