专栏文章
题解:P5018 [NOIP2018 普及组] 对称二叉树
P5018题解参与者 9已保存评论 11
文章操作
快速查看文章及其快照的属性,并进行相关操作。
- 当前评论
- 11 条
- 当前快照
- 1 份
- 快照标识符
- @miqn9k41
- 此快照首次捕获于
- 2025/12/04 07:34 3 个月前
- 此快照最后确认于
- 2025/12/04 07:34 3 个月前
前言
这么简单的 T4。
思路
只需要判断每个节点的子树是否为对称二叉树,然后计算该子树的节点个数就行了。
怎么判断是否为对称二叉树呢?先看一个图。
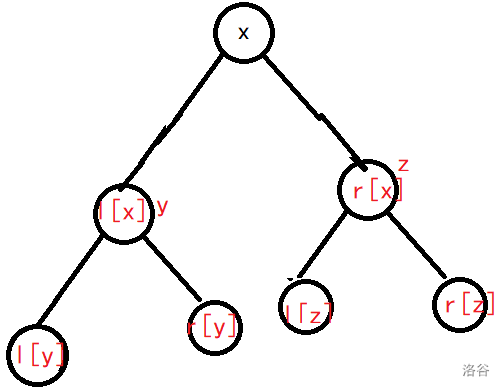

当到节点 时,需要满足 。到节点 和 时,需要满足 和 。若其中 其中一个的值为 或 不相等,那么它就不是对称二叉树。
AC 代码
CPP#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10;
int n,v[N],l[N],r[N],son[N];
bool dfs(int x,int y){
if(x==-1&&y==-1) return true;//都是叶子节点时满足条件
if(x==-1||y==-1) return false;//其中一个为叶子节点不满足
if(v[x]!=v[y]) return false;//v值不同不满足
return dfs(l[x],r[y])&&dfs(r[x],l[y]);
}
int count(int x){
if(x==-1) return 0;
son[x]=count(l[x])+count(r[x])+1;
return son[x];
}
int main(){
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&v[i]);
for(int i=1;i<=n;i++) scanf("%d%d",&l[i],&r[i]);
count(1); //计算子树的节点个数
int sum=0;
for(int i=1;i<=n;i++) if(dfs(i,i)) sum=max(sum,son[i]);
printf("%d\n",sum);
return 0;
}
相关推荐
评论
共 11 条评论,欢迎与作者交流。
正在加载评论...