题解：CF982F The Meeting Place Cannot Be Changed

https://www.luogu.com.cn/problem/CF982F

trick：对于环求交问题，可以先找到一个主环，然后对于环上的每一个节点找到不经过环上的边能够走到最远的节点，将这两个节点之间的点标记为不合法，只需要遍历每个节点一次。

由于某人会任意选择起点然后走无穷多步，说明图上的每一个节点都能够走到一个环上，要求必经之路相当于就是求这个有向图所有环的交。

求有关于环的问题，第一时间可能会想到 DFS 生成树，但有向图的 DFS 生成树并没有什么很好的性质，我们不得不抛弃这一想法。

有一步非常套路的想法是现在图上随便找一个环（题目保证一定有环），接着进行某些处理得到答案，笔者正是卡在了这一步。思考如何找到交是非常不容易的，正难则反，考虑能否找到不是交的边。

对于主环上每一个节点，我们可以找到其不经过环上的边能够走到的最远的节点，然后将这两个节点之间的节点标记为不合法，正确性是显然的，直接暴力做的时间复杂度是 $O(n^2)$。实际上每个节点第一次被访问到才是有意义的。如果一个节点第二次被访问，那么第二次访问到达的最远的节点一定是第一次访问到达的，所以我们证明了一个节点至多只会被访问一次。

但请读者认真思考一下便会发现上述证明其实是有误的，因为对于两个不同的节点 $A$ 和 $B$ 他们对“远”的定义不同，对于一个在 $A$ 和 $B$ 之间的节点 $C$，在 $A$ 作为起点时 $dis(A, C)$ 是要小于 $dis(B, C)$ 的，但在第一次访问的时候 $C$ 并不是访问到最远的节点，如下图所示：

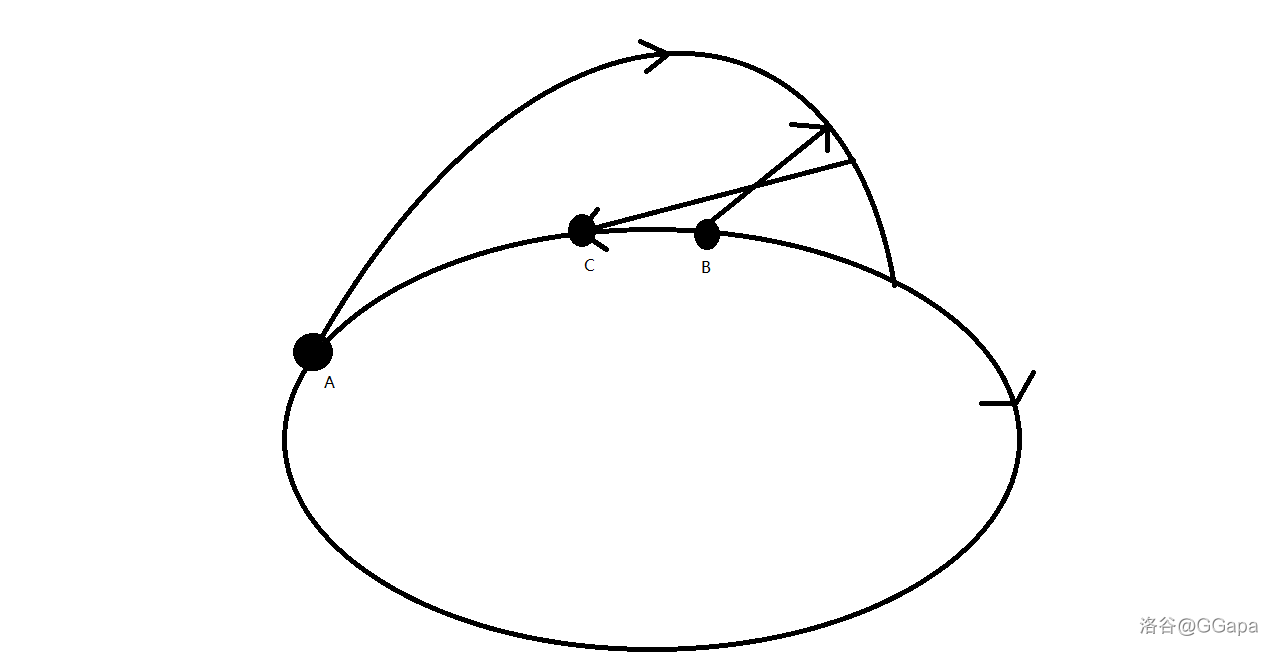
为了解决这个问题，我们不妨钦定原图一定有交，若原图一定有交那么上述策略可以得证，如果最终找到的交删去之后依然有环存在，则说明问题无解，需要在结尾加一个 check。