专栏文章

浅谈 ST 表

OOtachi
算法·理论参与者 3已保存评论 2

文章操作

快速查看文章及其快照的属性，并进行相关操作。

当前评论
2 条
当前快照
1 份
快照标识符
@mklf033r
此快照首次捕获于
2026/01/20 01:04
上个月
此快照最后确认于
2026/02/19 01:19
15 小时前
查看原文
ST 表（Sparse Table，稀疏表）是用于解决可重复贡献问题的数据结构。——OI Wiki

一维 RMQ

例题

P3865 【模板】ST 表 & RMQ 问题
显然，单次查询的时间复杂度应为 O(1)O(1)，并且预处理时间复杂度不能是 O(n2)O(n^2)。这个时候就可以考虑 ST 表了。
ST 表基于倍增思想。我们令 stj,ist_{j,i} 为区间 [i,i+2j−1][i,i+2^j-1] 的最大值，显然 st0,ist_{0,i} 为 aia_i。
为什么是 stj,ist_{j,i} 而不是 sti,jst_{i,j}？
在 stj,ist_{j,i} 中：内层循环变量是 ii，它是数组的最后一个维度。这意味着在内层循环时，CPU 访问的是一片连续的内存地址。这会极大提高 Cache Hit（缓存命中率），CPU 不需要频繁去主存（RAM）里抓数据。
在 sti,jst_{i,j} 中：内层循环变量是 ii，但 ii 是数组的第一个维度。每次循环，内存地址都会跳跃 21×421 \times 4 字节。这种“跳跃访问”对缓存非常不友好。

预处理

初始值方面显然 st0,i=aist_{0,i}=a_i。
作为倍增的一种实现，ST 表的思想和倍增可谓是一模一样。我们可以把 2j2^j 拆成 2j−1+2j−12^{j-1}+2^{j-1}，也就是把 [i,i+2j−1][i,i+2^j-1] 拆成 [i,i+2j−1−1][i,i+2^{j-1}-1] 和 [i+2j−1,i+2j−1][i+2^{j-1},i+2^j-1] 两部分，那么 stj,i=max⁡(stj−1,i,stj−1,i+2j−1)st_{j,i}=\max(st_{j-1,i},st_{j-1,i+2^{j-1}})。

查询

对于每个询问 [l,r][l,r]，可以拆成两部分：[l,l+2s−1][l,l+2^s-1] 和 [r−2s+1,r][r-2^s+1,r]。其中 s=⌊log⁡2(r−l+1)⌋s=\left \lfloor \log_2 (r-l+1) \right \rfloor。两部分的最大值就是答案。

代码实现

请注意，如果你要求 ⌊log⁡2n⌋\left \lfloor \log_2 n \right \rfloor，不建议使用 log2(n)，因为该函数常数较大，而且有潜在的精度误差风险，所以建议使用 __lg(n)。
AC CodeCPP
int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++)
		scanf("%d",&st[0][i]);
	for(int j=1;j<=__lg(n);j++)
		for(int i=1;i+(1<<j)-1<=n;i++)
			st[j][i]=max(st[j-1][i],st[j-1][i+(1<<j-1)]);
	while(m--)
	{
		int l,r;
		scanf("%d%d",&l,&r);
		int k=__lg(r-l+1);
		printf("%d\n",max(st[k][l],st[k][r-(1<<k)+1]));
	}
	return 0;
}

时空复杂度

预处理时间复杂度 O(nlog⁡n)O(n \log n)，单次查询时间复杂度 O(1)O(1)。
空间复杂度 O(nlog⁡n)O(n \log n)。

习题

P1890 gcd 区间
因为满足 gcd⁡(x,x)=x\gcd(x,x)=x，所以可以用 ST 表维护。
P1886 【模板】单调队列 / 滑动窗口
你说得对，这道题正解应该是单调队列，但是也没人拦我用 ST 表啊！

二维 RMQ

关于二维 RMQ 的实现方法
其实二维 RMQ 有两种实现：一种是分步合并（先算行再合并列），一种是四项合并。理论上是分步合并更好，但是我选择的是四项合并。两者的优缺点显示如下：
分步合并四项合并
比较次数较少。11 次 max⁡\max 即可。较多。33 次 max⁡\max 导致常数较大。
代码实现极其简洁。逻辑线性，不需要处理复杂的边界。较为繁琐。必须手动处理边界的情况。
逻辑直观度略显抽象。先处理宽再处理长。非常直观。四个小方块拼成大方块，符合几何直觉。
鲁棒性高。不容易出现数组越界或逻辑遗漏。中。初始化边界条件时极易出错。

例题（正方形）

P2216 [HAOI2007] 理想的正方形
令 stk,i,jst_{k,i,j} 为以 (i,j)(i,j) 为左上角，大小 2k×2k2^k \times 2^k 的正方形的最值。

预处理

我们可以分别把长和宽拆成 2k−1+2k−12^{k-1}+2^{k-1}，所以可以得到：
stk,i,j=max⁡{stk−1,i,jstk−1,i,j+2k−1stk−1,i+2k−1,jstk−1,i+2k−1,j+2k−1st_{k,i,j}=\max\left\{\begin{matrix}st_{k-1,i,j} \\st_{k-1,i,j+2^{k-1}} \\st_{k-1,i+2^{k-1},j} \\st_{k-1,i+2^{k-1},j+2^{k-1}} \end{matrix}\right.

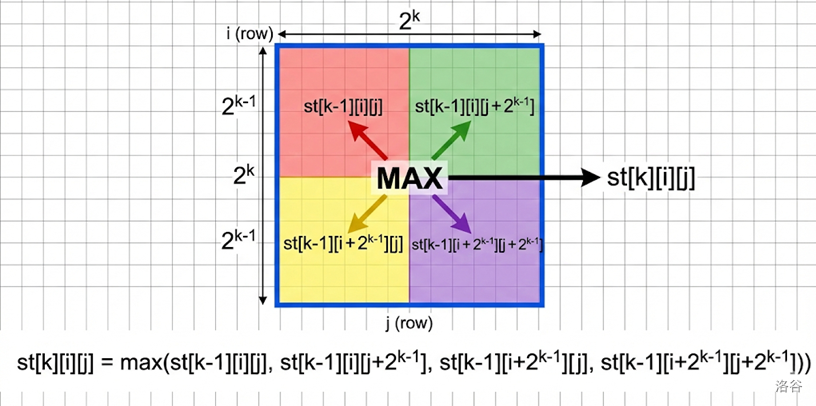
查询

假设要求左上角 (x1,y1)(x1,y1)，右下角 (x2,y2)(x2,y2) 的正方形的最值。 令 k=⌊log⁡2L⌋k=\lfloor \log_2 L \rfloor。这里 LL 是正方形的边长。依旧把长和宽拆成 2k−1+2k−12^{k-1}+2^{k-1}，可以得到所求值应为：
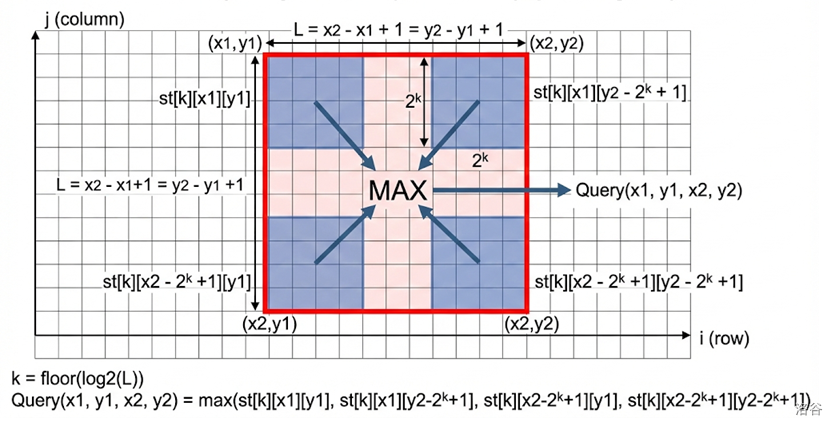
Ans=max⁡{stk,x1,y1stk,x1,y2−2k+1stk,x2−2k+1,y1stk,x2−2k+1,y2−2k+1Ans=\max\left\{\begin{matrix}st_{k,x1,y1} \\st_{k,x1,y2-2^k+1} \\st_{k,x2-2^k+1,y1} \\st_{k,x2-2^k+1,y2-2^k+1} \end{matrix}\right.

代码实现

AC CodeCPP
#include<bits/stdc++.h>
using namespace std;
const int N=1005;
int a,b,n;
int stmax[15][N][N],stmin[15][N][N];
int ans=INT_MAX;
int main()
{
    scanf("%d%d%d",&a,&b,&n);
    for(int i=1;i<=a;i++)
        for(int j=1;j<=b;j++)
        {
            int x;
            scanf("%d",&x);
            stmax[0][i][j]=stmin[0][i][j]=x;
        }
    for(int k=1;k<=__lg(min(a,b));k++)
        for(int i=1;i+(1<<k)-1<=a;i++)
            for(int j=1;j+(1<<k)-1<=b;j++)
            {
                stmax[k][i][j]=max({stmax[k-1][i][j],stmax[k-1][i][j+(1<<k-1)],stmax[k-1][i+(1<<k-1)][j],stmax[k-1][i+(1<<k-1)][j+(1<<k-1)]});
                stmin[k][i][j]=min({stmin[k-1][i][j],stmin[k-1][i][j+(1<<k-1)],stmin[k-1][i+(1<<k-1)][j],stmin[k-1][i+(1<<k-1)][j+(1<<k-1)]});
            }
    for(int i=1;i+n-1<=a;i++)
        for(int j=1;j+n-1<=b;j++)
        {
            int k=__lg(n);
            int maxn=max({stmax[k][i][j],stmax[k][i][j+n-(1<<k)],stmax[k][i+n-(1<<k)][j],stmax[k][i+n-(1<<k)][j+n-(1<<k)]});
            int minn=min({stmin[k][i][j],stmin[k][i][j+n-(1<<k)],stmin[k][i+n-(1<<k)][j],stmin[k][i+n-(1<<k)][j+n-(1<<k)]});
            ans=min(ans,maxn-minn);
        }
    printf("%d\n",ans);
    return 0;
}
不得不说，虽然 ST 表相较于正解单调队列多了一个 log⁡\log，但是胜在简洁，代码好调试。
其实这段代码是可以用滚动数组优化的（即把第一维舍掉），读者可以自行了解。其实也就是空间复杂度少了个 log⁡\log。

习题（正方形）

P2701 [USACO5.3] 巨大的牛棚 Big Barn
发现边长满足单调性，因此考虑二分答案结合 ST 表。
时间复杂度较正解 DP 多了一个 log⁡\log。
AC CodeCPP
#include<bits/stdc++.h>
using namespace std;
const int N=1005;
int n,m;
bool st[15][N][N];
bool check(int mid)
{
    for(int i=1;i+mid-1<=n;i++)
        for(int j=1;j+mid-1<=n;j++)
        {
            int k=__lg(mid);
            bool flag=st[k][i][j]||st[k][i+mid-(1<<k)][j]||st[k][i][j+mid-(1<<k)]||st[k][i+mid-(1<<k)][j+mid-(1<<k)];
            if(!flag)
                return true;
        }
    return false;
}
int main()
{
    scanf("%d%d",&n,&m);
    while(m--)
    {
        int x,y;
        scanf("%d%d",&x,&y);
        st[0][x][y]=true;
    }
    for(int k=1;k<=10;k++)
        for(int i=1;i+(1<<k)-1<=n;i++)
            for(int j=1;j+(1<<k)-1<=n;j++)
            {
                st[k][i][j]|=st[k-1][i][j];
                st[k][i][j]|=st[k-1][i+(1<<k-1)][j];
                st[k][i][j]|=st[k-1][i][j+(1<<k-1)];
                st[k][i][j]|=st[k-1][i+(1<<k-1)][j+(1<<k-1)];
            }
    int l=1,r=n,mid;
    while(l<r)
    {
        mid=l+r+1>>1;
        if(check(mid))
            l=mid;
        else
            r=mid-1;
    }
    printf("%d\n",l);
    return 0;
}

例题（长方形）

Check Corners
令 stki,kj,i,jst_{ki,kj,i,j} 为以 (i,j)(i,j) 为左上角，大小 2ki×2kj2^{ki} \times 2^{kj} 的长方形的最大值。

预处理

把长拆成 2ki−1+2ki−12^{ki-1}+2^{ki-1}，宽拆成 2kj−1+2kj−12^{kj-1}+2^{kj-1}。可以得到：
stki,kj,i,j=max⁡{stki−1,kj−1,i,jstki−1,kj−1,i+2ki−1,jstki−1,kj−1,i,j+2kj−1stki−1,kj−1,i+2ki−1,j+2kj−1st_{ki,kj,i,j}=\max\left\{\begin{matrix}st_{ki-1,kj-1,i,j} \\st_{ki-1,kj-1,i+2^{ki-1},j} \\st_{ki-1,kj-1,i,j+2^{kj-1}} \\st_{ki-1,kj-1,i+2^{ki-1},j+2^{kj-1}} \end{matrix}\right.
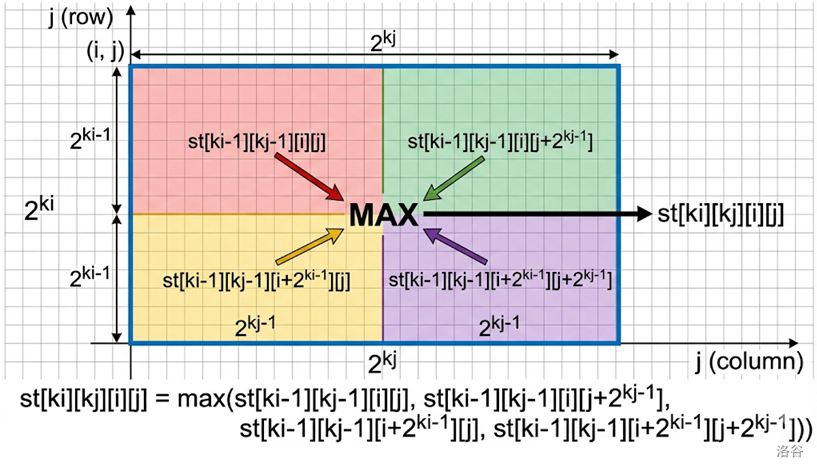
还有注意处理边界情况：st0,0,i,j=ai,jst_{0,0,i,j}=a_{i,j}，对任意的 st0,kj,i,jst_{0,kj,i,j} 和 stki,0,i,jst_{ki,0,i,j} 再分别跑一遍一维 RMQ。

查询

假设要求左上角 (x1,y1)(x1,y1)，右下角 (x2,y2)(x2,y2) 的正方形的最值。 令 ki=⌊log⁡2Li⌋,kj=⌊log⁡2Lj⌋ki=\lfloor \log_2 L_i \rfloor,kj=\lfloor \log_2 L_j \rfloor。这里 LiL_i 是长方形的长，LjL_j 是长方形的宽。还是把长和宽拆开，可以得到：
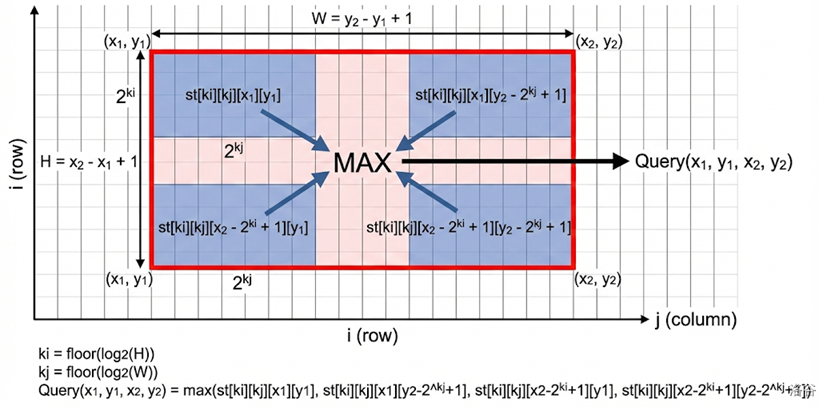
Ans=max⁡{stki,kj,x1,y1stki,kj,x1,y2−2kj+1stki,kj,x2−2ki+1,y1stki,kj,x2−2ki+1,y2−2kj+1Ans=\max\left\{\begin{matrix}st_{ki,kj,x1,y1} \\st_{ki,kj,x1,y2-2^{kj}+1} \\st_{ki,kj,x2-2^{ki}+1,y1} \\st_{ki,kj,x2-2^{ki}+1,y2-2^{kj}+1} \end{matrix}\right.

代码实现

注意 HDU 非常坑。多组数据，不能用 __lg()，也不能用万能头。
AC CodeCPP
#include<cstdio>
#include<algorithm>
using namespace std;
const int N=305;
int n,m,q;
int lg[N];
int st[10][10][N][N]; 
int main()
{
	lg[1]=0;
	for(int i=2;i<=300;i++)
		lg[i]=lg[i>>1]+1;
	while(~scanf("%d%d",&n,&m))
	{	
		for(int i=1;i<=n;i++)
			for(int j=1;j<=m;j++)
				scanf("%d",&st[0][0][i][j]);
		//处理1*2^kj 
		for(int kj=1;kj<=lg[m];kj++)
			for(int i=1;i<=n;i++)
				for(int j=1;j+(1<<kj)-1<=m;j++)
					st[0][kj][i][j]=max(st[0][kj-1][i][j],st[0][kj-1][i][j+(1<<kj-1)]);
		//处理2^ki*1
		for(int ki=1;ki<=lg[n];ki++)
			for(int i=1;i+(1<<ki)-1<=n;i++)
				for(int j=1;j<=m;j++)
					st[ki][0][i][j]=max(st[ki-1][0][i][j],st[ki-1][0][i+(1<<ki-1)][j]);
		//处理正常情况
		for(int ki=1;ki<=lg[n];ki++)
			for(int kj=1;kj<=lg[m];kj++)
				for(int i=1;i+(1<<ki)-1<=n;i++)
					for(int j=1;j+(1<<kj)-1<=m;j++)
						st[ki][kj][i][j]=max({st[ki-1][kj-1][i][j],st[ki-1][kj-1][i+(1<<ki-1)][j],st[ki-1][kj-1][i][j+(1<<kj-1)],st[ki-1][kj-1][i+(1<<ki-1)][j+(1<<kj-1)]});
		scanf("%d",&q);
		while(q--)
		{
			int x1,y1,x2,y2;
			scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
			int ki=lg[x2-x1+1],kj=lg[y2-y1+1];
			int maxn=max({st[ki][kj][x1][y1],st[ki][kj][x2-(1<<ki)+1][y1],st[ki][kj][x1][y2-(1<<kj)+1],st[ki][kj][x2-(1<<ki)+1][y2-(1<<kj)+1]});
			printf("%d %s\n",maxn,max({st[0][0][x1][y1],st[0][0][x1][y2],st[0][0][x2][y1],st[0][0][x2][y2]})==maxn?"yes":"no");
		}	
	} 
	return 0;
}

时空复杂度

正方形：预处理时间复杂度 O(n2log⁡n)O(n^2 \log n)，单次查询时间复杂度 O(1)O(1)。空间复杂度 O(nmlog⁡min(n,m))O(nm \log min(n,m))
长方形：预处理时间复杂度 O(nmlog⁡nlog⁡m)O(nm \log n \log m)，单次查询时间复杂度 O(1)O(1)。空间复杂度 O(nmlog⁡nlog⁡m)O(nm \log n \log m)。

局限性

ST 表的优点是好写而且单次 O(1)O(1)；缺点是只能维护静态，而且二维 RMQ 有巨大的空间开销，需要预防潜在的 MLE。与同样静态的猫树相比，它只能维护可重复贡献的运算。如果有修改的话，建议用树状数组/线段树。
顺便安利一下自己的树状数组。

评论

共 2 条评论，欢迎与作者交流。

正在加载评论...