专栏文章

题解： AT_abc391_d [ABC391D] Gravity

FFlowerAccepted
AT_abc391_d题解参与者 27已保存评论 29

文章操作

快速查看文章及其快照的属性，并进行相关操作。

当前评论
29 条
当前快照
1 份
快照标识符
@miqcvffy
此快照首次捕获于
2025/12/04 02:43
3 个月前
此快照最后确认于
2025/12/04 02:43
3 个月前
查看原文

解题思路

注意到落下的正方形们满一行才会被消除，之后的正方形才会落下来。所以能清除多少行正方形和正方形们初始的高度无关，而是等于同一个 XX 中最少有多少个正方形。如图 S-AT_abc391_d-1\text{S-AT\_abc391\_d-1} 所示，没有正方形会被消除：
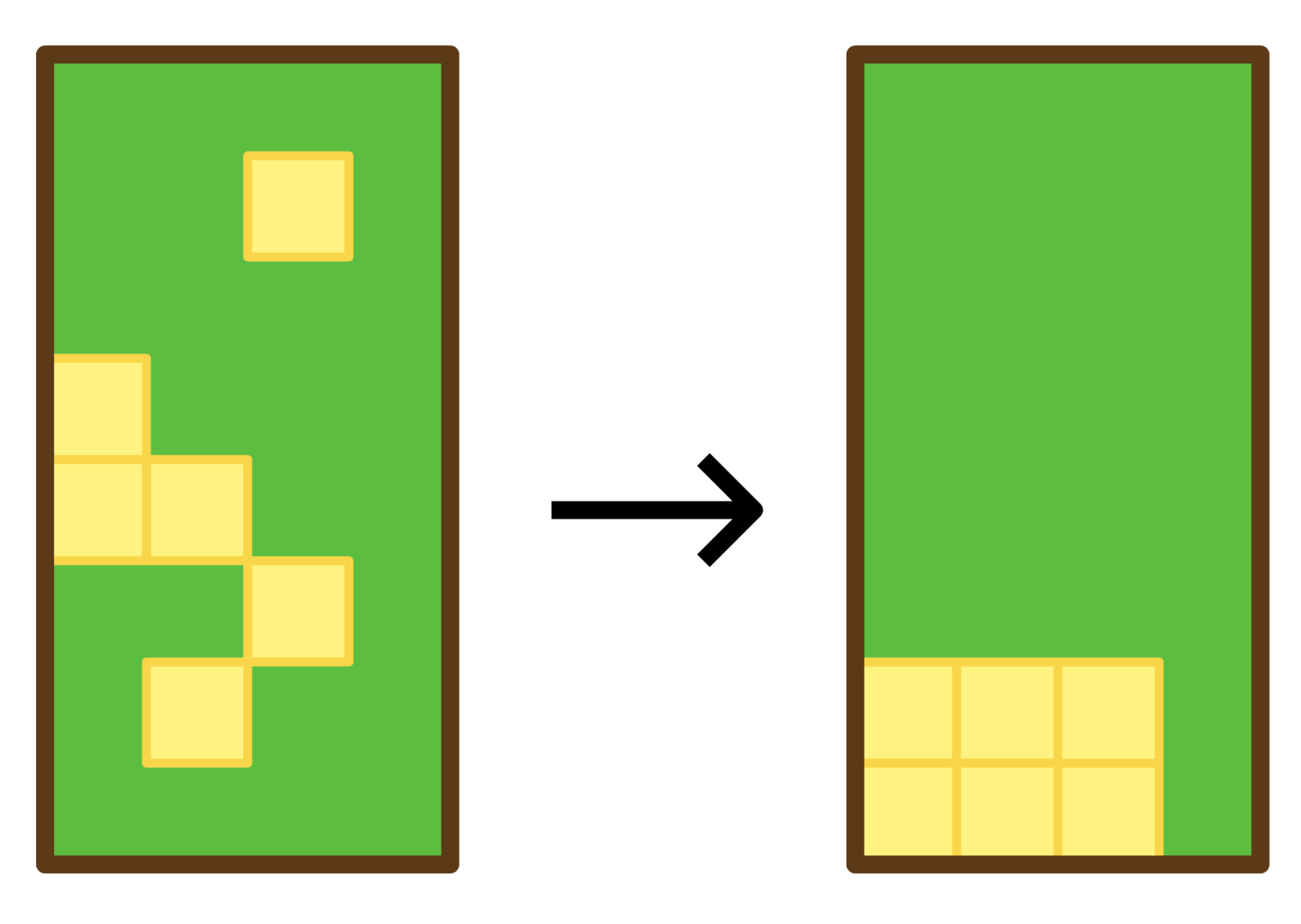
图 S-AT_abc391_d-1这个形状，这个颜色.....也许有些熟悉\footnotesize \text{图 S-AT\_abc391\_d-1} \\ \text{这个形状，这个颜色.....也许有些熟悉}
在加入一个绿色正方形后，最底部的一行才会被消除，如图 S-AT_abc391_d-2\text{S-AT\_abc391\_d-2} 所示：
图 S-AT_abc391_d-2送走底部正方形，你想到了什么？\footnotesize \text{图 S-AT\_abc391\_d-2} \\ \text{送走底部正方形，你想到了什么？}
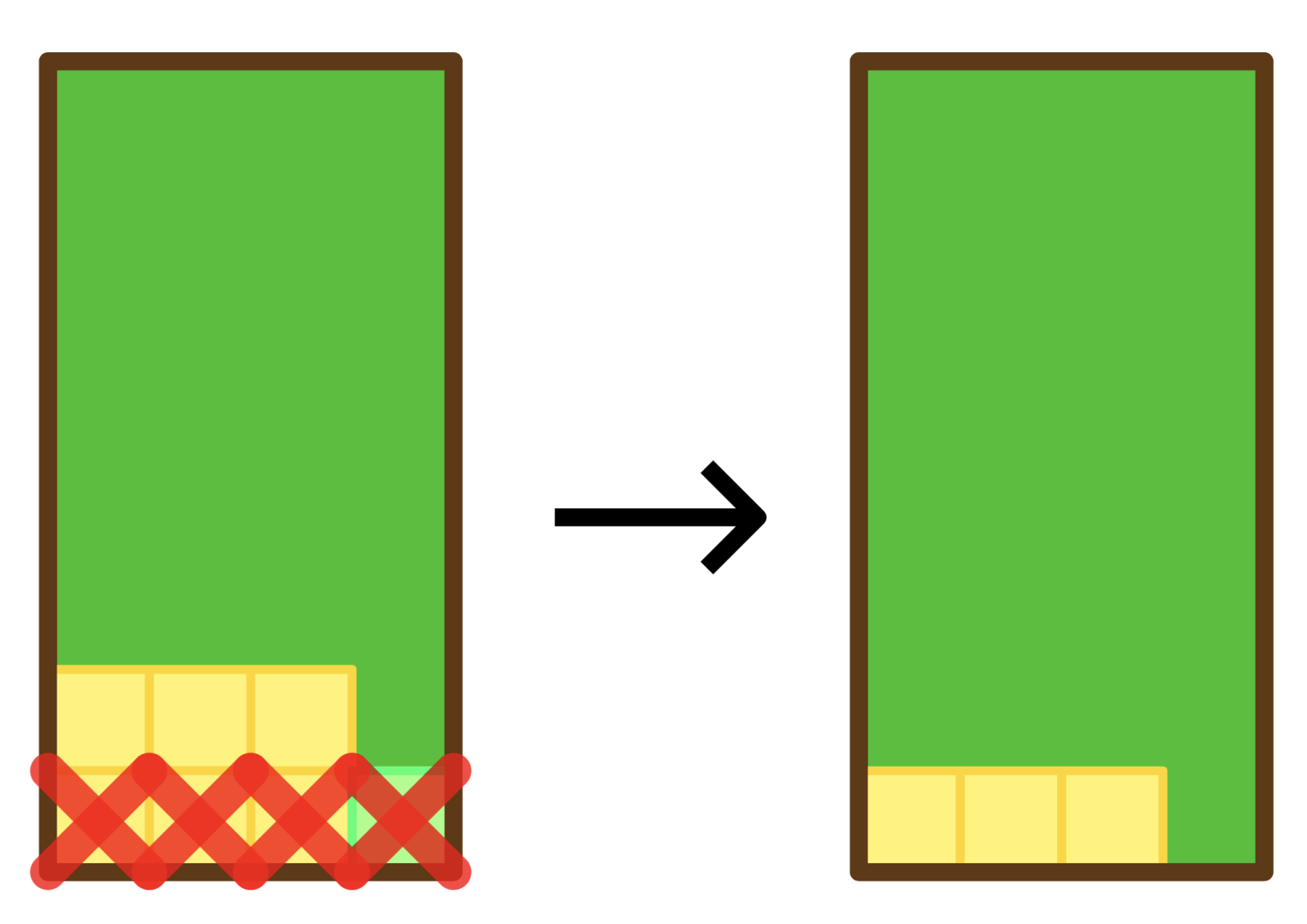
我们可以使用一个 vector<int> v[MAXM]v[MAXM] 来存储每一列从低到高的正方形。
具体的，可以按顺序输入到两个 pair<int, int> 数组 a[MAXN]a[MAXN] 和 b[MAXN]b[MAXN]，将 XiX_i 输入到 ai.firsta_i.first（）；将 YiY_i 输入到 ai.seconda_i.second，再将 aa 拷贝一份到 bb，以便后用。（当然输入到 bb，拷贝到 aa 也是一样的。）
再将 aa 按 secondsecond 不降序排序，这需要自定义比较函数
CPP
bool cmp(pair<int, int> x, pair<int, int> y) {
    return x.second < y.second;
}
再使用 sort(a + 1, a + n + 1, cmp) 进行排序。当然，你要愿意手搓 STL\tt STL 我也不会拦你。
然后按顺序遍历 aa 数组，∀1≤i≤N\forall 1 \le i \le N，在 vai.firstv_{a_i.first} 的尾部追加 ai.seconda_i.second，这样保证了表示每一列的向量中，下标越大的正方形越高，即正方形的高度呈升序排列，代码如下：
CPP
for (int i = 1; i <= n; i ++) {
    v[a[i].first].push_back(a[i].second);
}
图 S-AT_abc391_d-1\text{S-AT\_abc391\_d-1} 处理前后如图 S-AT_abc391_d-3\text{S-AT\_abc391\_d-3} 所示：
图 S-AT_abc391_d-3醍醐灌顶？\footnotesize \text{图 S-AT\_abc391\_d-3} \\ \text{醍醐灌顶？}
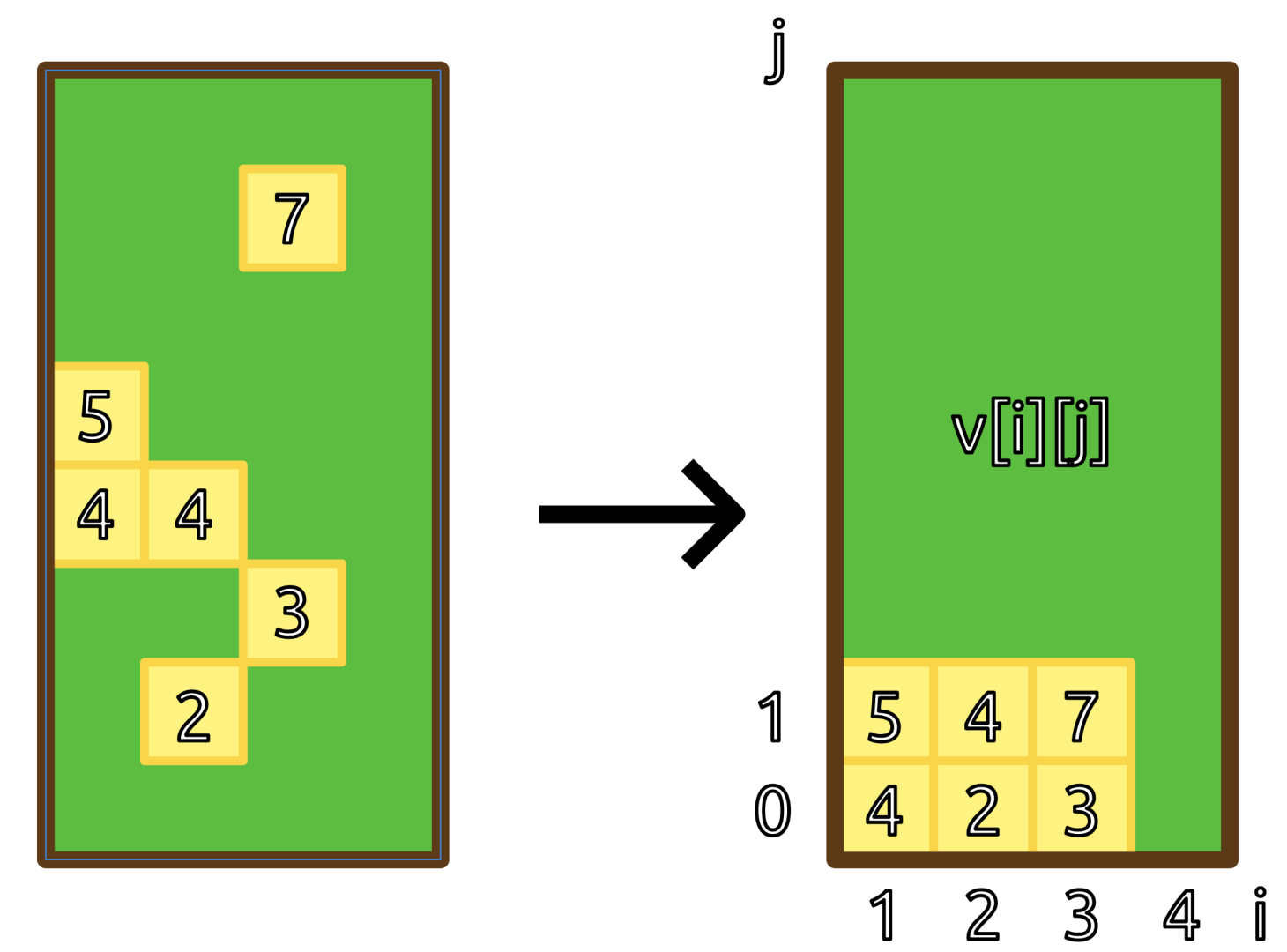
记 minsmins 为每个 viv_i 中最少有多少个正方形；maxsmaxs 为每个 viv_i 中最多有多少个正方形。
图 S-AT_abc391_d-1\text{S-AT\_abc391\_d-1} 中，mins=0mins = 0，maxs=2maxs = 2；图 S-AT_abc391_d-3\text{S-AT\_abc391\_d-3} 中，mins=1mins = 1，maxs=2maxs = 2;
我们开一个大小为 maxsmaxs 的向量 tt，记录每一层正方形的消失时间，
∀0≤i<maxs,ti={max⁡j=1Wvj,ii<minsinf⁡otherwise⁡\forall 0 \le i < maxs, \\ t_i = \begin{cases} \max\limits_{j = 1}^W v_{j, i} & i < mins \\ \inf & \operatorname{otherwise} \end{cases}
这里 inf⁡\inf 取 1e9+5 即可。
看不懂？上代码！
CPP
t.resize(maxs + 5); // 开大一点
for (int j = 1; j <= w; j ++) {
    for (int i = 0; i < mins; i ++) {
        t[i] = max(t[i], v[j][i]);
    }
}
for (int i = mins; i < maxs; i ++) {
    t[i] = 1e9 + 5;
}
还看不懂？上图片！
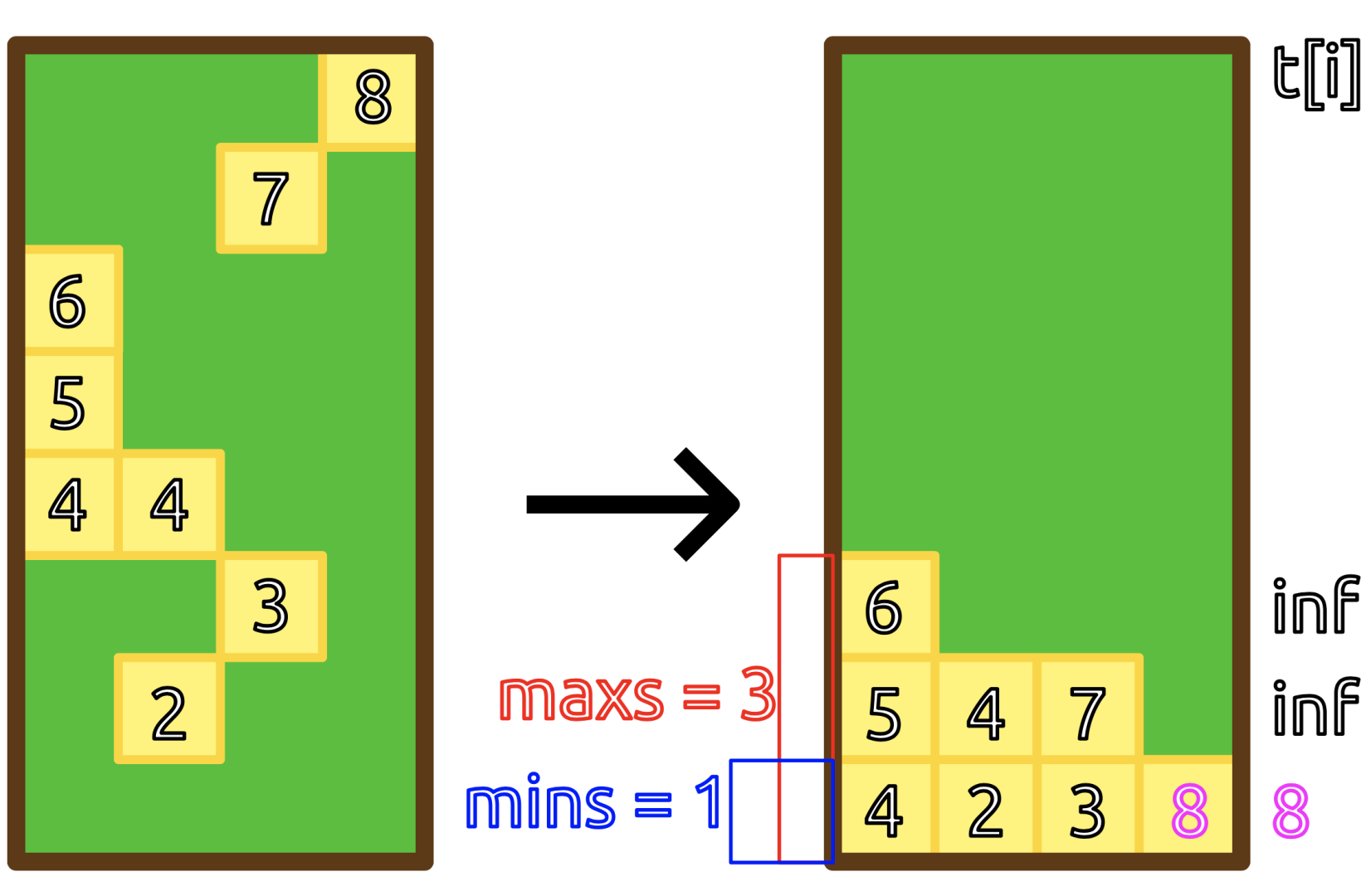
图 S-AT_abc391_d-4你，学会了吗？\footnotesize \text{图 S-AT\_abc391\_d-4} \\ \text{你，学会了吗？}
预处理完毕，开是处理询问。
对于每个询问，首先注意输入顺序。（编者被坑了！）
接着找到对应的正方形对应的层数 idid，一定要使用原来顺序的 bb 数组查找。这可以使用 lower_bound 来优化，返回的是指针，注意减去开头：
CPP
id = (int)(lower_bound(v[b[A].first].begin(), v[b[A].first].end(), b[A].second) - v[b[A].first].begin());
然后注意到正方形若在 TiT_i 时刻没有正在消失，那么它在 Ti+0.5T_i + 0.5 时刻就还存在。
最后，根据预处理的结论，判断 TiT_i 是否小于 tidt_{id} 即可。如果 id≥minsid \ge mins，说明这层没凑齐，正方形自然就不会下落了，TiT_i 不会超过 inf⁡\inf（109+510^9+5）。
这块内容如果不理解还请看看图 S-AT_abc391_d-4\text{S-AT\_abc391\_d-4}。

代码呈现

代码不丑，请参考。
CPP
#include <algorithm>
#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector> // 万能头不是 STL 成员，咱不用。
using namespace std;

pair<int, int> a[200005], b[200005];
vector<int> v[200005], t; // 防止越界，开大数组，从我做起

bool cmp(pair<int, int> x, pair<int, int> y) { // 比较数对
    return x.second < y.second;
}

int main() {
    int n, w, mins = 1e9+5, maxs = 0, q, A, T, id;
    cin >> n >> w;
    for (int i = 1; i <= n; i ++) {
        cin >> b[i].first >> b[i].second;
        a[i] = b[i];
    } // 输入
    sort(a + 1, a + n + 1, cmp);
    for (int i = 1; i <= n; i ++) {
        v[a[i].first].push_back(a[i].second);
    } // 离散化？？
    for (int i = 1; i <= w; i ++) {
        mins = min(mins, (int)v[i].size());
        maxs = max(maxs, (int)v[i].size());
    } // 计算层数
    t.resize(maxs + 5);
    for (int j = 1; j <= w; j ++) {
        for (int i = 0; i < mins; i ++) {
            t[i] = max(t[i], v[j][i]);
        }
    } // 计算每一层的消失时间
    for (int i = mins; i < maxs; i ++) {
        t[i] = 1e9 + 5;
    } // inf
    cin >> q;
    for (int i = 1; i <= q; i ++) {
        cin >> T >> A;
        id = (int)(lower_bound(v[b[A].first].begin(), v[b[A].first].end(), b[A].second) - v[b[A].first].begin()); // 二分
        cout << (T < t[id] ? "Yes\n" : "No\n"); // 换行！
    }
    return 0;
}
至此，本题 Accepted。

复杂度分析

预处理除排序外的均摊复杂度是 O(N)O(N)，这是因为无论单层还是双层的循环，总的循环次数也不会也不会超过 NN 次。
STL\tt STL 排序的时间复杂度是 O(Nlog⁡N)O(N \log N)。（当然，这个排序也许不会执行哒）
而每个询问也许会查询到一个有近乎 NN 个正方形的 XX 坐标，由于二分查找的优化，最坏情况下查询的总时间复杂度是 O(Qlog⁡N)O(Q \log N)，最好情况下则是只有 11 层，最好情况下查询的总时间复杂度就是 O(Q)O(Q)。
综合来看，程序的最好时间复杂度是 O(N+Q)O(N + Q)，最坏的则是 O((N+Q)log⁡N)O((N + Q) \log N)，轻松通过！
其实 STL\tt STL 在此题中发挥了挺大的作用，不然这题的代码就有上千行喽！STL\tt STL 好闪，拜谢 STL\tt STL！
这篇题解花了我一天的心血，求个赞！

评论

共 29 条评论，欢迎与作者交流。

正在加载评论...