专栏文章
P11239 [KTSC 2024 R2] 跳跃游戏 - Solution
P11239题解参与者 1已保存评论 0
文章操作
快速查看文章及其快照的属性,并进行相关操作。
- 当前评论
- 0 条
- 当前快照
- 1 份
- 快照标识符
- @minagfs1
- 此快照首次捕获于
- 2025/12/01 23:12 3 个月前
- 此快照最后确认于
- 2025/12/01 23:12 3 个月前
感觉有点不明所以的题。
以下序列均为 1-index,假设 ,如果不是那么将序列末尾补 即可,显然不影响复杂度。
首先 的 dp 是显然的,考虑类似序列最大权独立集的转移就行。 为只考虑前 个元素的得分,,令 。
然后我们要在一个长度极长的序列上做这个东西,当然只能离散化,然后将极长相邻 相同的元素缩在一起,最后会得到一个长度 的序列,这是显然的(每次区间加,该序列长度至多加 )。
直接对着原序列做,讨论非常复杂,考虑将原序列按下标模 分组,此时我们可以将原序列写为 个长度为 的序列,转移一个 的时候:
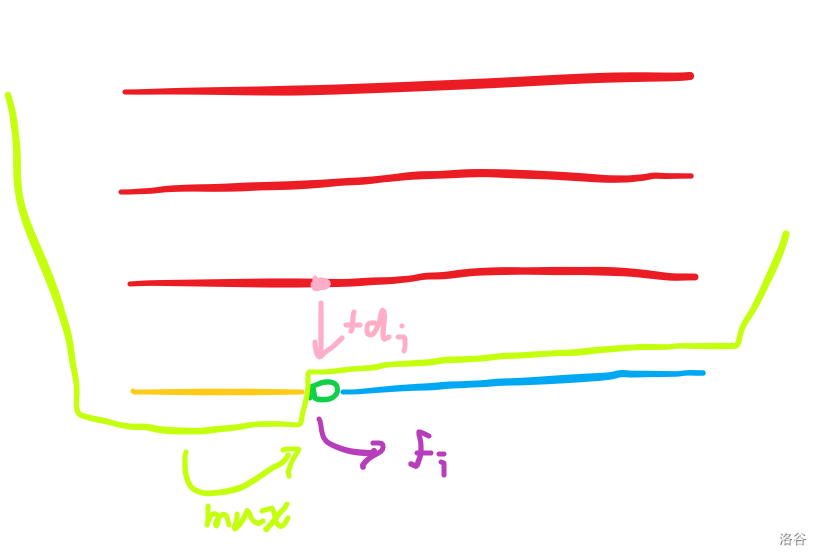
它可能来自上一层相同位置 ,也可能取自前面已计算完的所有 的最大值。
-
已计算完毕的 单调不降,这是显然的,所以我们只用考虑上一层的 。我们默认在线段树里面先将所有的 加好,这是若干个区间加,均摊 个。
-
我们的 要么来自上一层 ,要么来自本序列的前面的某个 。考虑这种差异的原因,当然是因为 (或者 继承过来的更大),导致 往后的一段 跟 相同的元素 取 更优秀。由于 具有单调性,这必然是 开头的一段区间,可以线段树上二分求出,然后做区间覆盖。
-
不难发现,对于 相同的相邻的 ,不可能后面的取 前面却不取,所以只考虑 等价段开头的 即可。
-
还有一个问题,我们现在的复杂度是 , 很小怎么办。
注意到有些层它们内部只有一个种类的 ,这时候我们就是线段树全局加若干个 ,来将一段非常长的相同的 快速做完。
时空复杂度 ,可以通过。
这个做法常数比较大而且细节不少,代码等有时间写的时候放在评论区。
相关推荐
评论
共 0 条评论,欢迎与作者交流。
正在加载评论...