专栏文章

题解：P12480 [集训队互测 2024] Classical Counting Problem

yyishanyi
P12480题解参与者 2已保存评论 1

文章操作

快速查看文章及其快照的属性，并进行相关操作。

当前评论
1 条
当前快照
1 份
快照标识符
@mior56l8
此快照首次捕获于
2025/12/02 23:47
3 个月前
此快照最后确认于
2025/12/02 23:47
3 个月前
查看原文

[Luogu P12480]/[QOJ9533] Classical Counting Problem

pro.

nn 个点的无根树，每次可以做以下操作若干次：
  • 选择当前树上编号最大或最小的点 uu，删去 uu 及其连边，保留任意一个连通块作为操作后的树。
令 minmin 为树上所有节点编号的最小值，maxmax 为树上所有节点编号的最大值，sizesize 为树上的节点个数，则一棵树的权值为 min⋅max⋅sizemin\cdot max\cdot size。
求所有能通过操作得到的非空树的权值和。
n≤1e5n\le1e5。3s,1024MB\mathrm{3s,1024MB}。

sol.

读完题后发现没有明显的多项式做法，考虑寻找性质。
不很容易发现：一对合法的 (min,max)(min,max) 可以确定唯一的一棵树。
证明：一对点 (u,v)(u,v) 能作为一棵合法树的 (min,max)(min,max) 当且仅当 uu 到 vv 的路径上的所有点都在 [u,v][u,v] 区间内，然后在这条路径上不断加入在 [u,v][u,v] 区间内且与当前联通块联通的点，即可得到 (u,v)(u,v) 对应的树 TT，显然树 TT 的形态与加点顺序无关，故每个合法 (u,v)(u,v) 对应唯一的一棵树。而对于一棵树 TT ，设其最小值和最大值分别为 (u,v)(u,v)，由于只对最大值或最小值操作，故再进行操作显然不对应 (u,v)(u,v) 。故合法 (min,max)(min,max) 与合法的树一一对应。
于是可以枚举 min,maxmin,max ，然后加入 [min,max][min,max] 区间内的点，判断是否联通并统计答案。暴力实现 O(n3)\mathcal{O}(n^3) ，固定 minmin 或 maxmax 再依次加入点，用并查集维护连通性，即可实现 O(n2)\mathcal{O}(n^2) 。
考虑优化。注意到一对合法 (min,max)(min, max) 的判断用到了路径信息，于是想到点分治。对于一个分治中心，记录每个点到其路径上的最大值 maxumax_u 和最小值 minumin_u，则对于 u=minu∧v=maxv∧minv≥u∧maxu≤vu=min_u\land v=max_v\land min_v\ge u\land max_u\le v 的 (u,v)(u,v) 即为合法对。如果没有 sizesize 可以二维数点维护，难点在于怎么处理 sizesize 这一项。
Trick：对于难处理的有限制联通块大小，可以考虑拆贡献，即维护有多少个 xx 能满足这样的限制。
于是可以转化为在每个分治中心下统计有多少个 (l,r,x)(l,r,x) 可以在同一个联通块里，对答案的贡献即为 l⋅rl\cdot r。
显然合法 l,rl,r 的限制依然成立，而 xx 需要满足的限制应该为 minx≥l∧maxx≤rmin_x\ge l\land max_x\le r。
即一对合法 (l,r,x)(l,r,x) 应满足：
{minl=lmaxr=rminl≤minxminl≤minrmaxx≤maxrmaxl≤maxr\begin{cases} min_l=l \\ max_r=r \\ min_l\le min_x \\ min_l\le min_r \\ max_x\le max_r \\ max_l\le max_r \end{cases}
观察到关键限制都是 minmin 或 maxmax 之间的偏序关系，于是不妨设每个点的坐标为 (minx,maxx)(min_x,max_x) ，发现合法三元组在二维平面上应满足：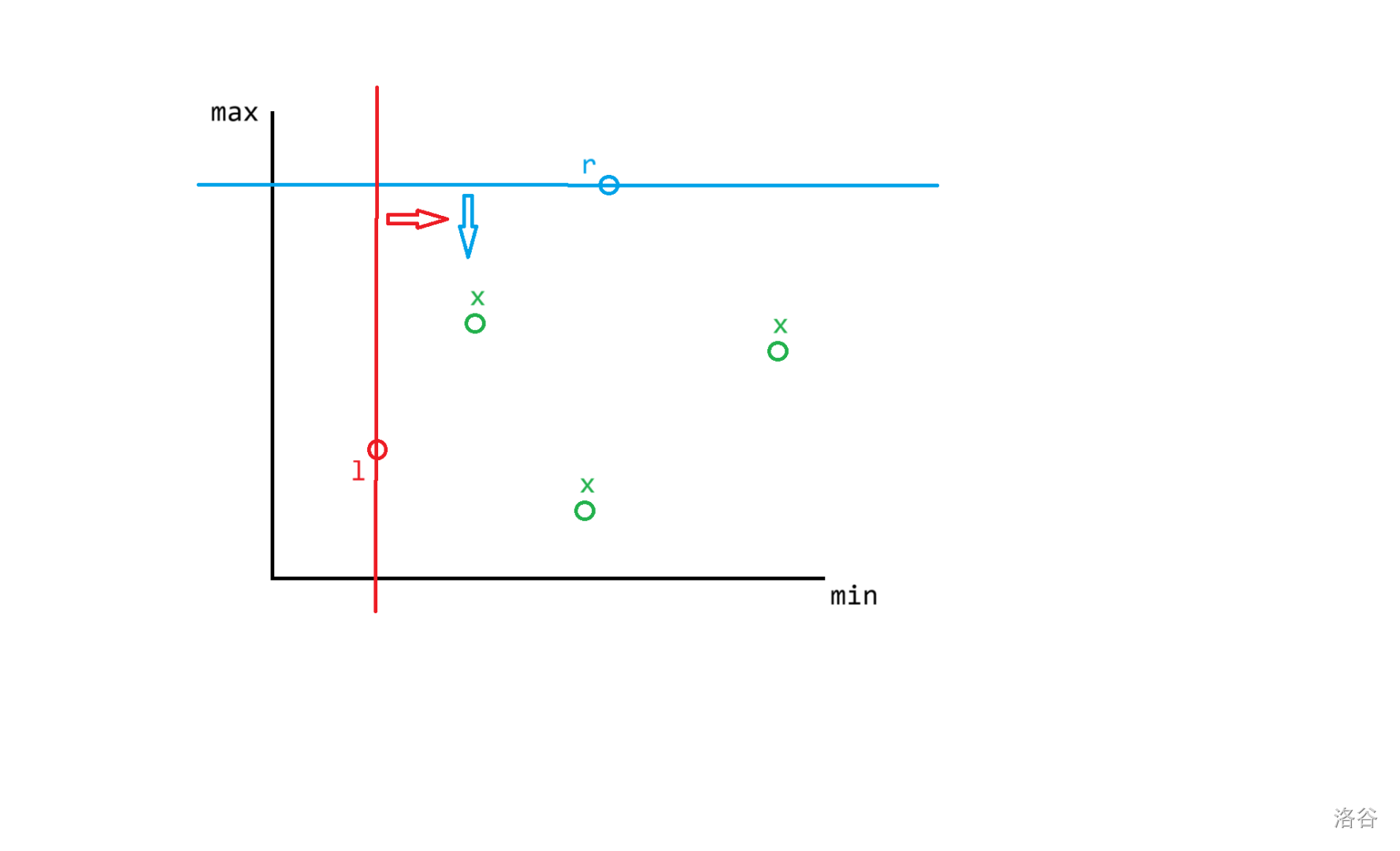
考虑对 maxmax 一维扫描线，线段树维护另一维。
于是当扫到某个 rr 时，能与 rr 匹配的 (l,x)(l,x) 一定已经加入了线段树。
而对于某个 rr ，能与它产生贡献的 ll 一定在 minrmin_r 左侧。设 ll 能与 cntlcnt_l 个 xx 匹配，则答案为 l⋅cntl⋅rl\cdot cnt_l\cdot r 。
所以线段树需要维护区间 ∑l⋅cntl\sum l\cdot cnt_l 。
我们设一段区间内可以作为 ll 的点的编号和为标准和 stdstd，要求的 ∑l⋅cntl\sum l\cdot cnt_l 为结果和 sumsum 。
则插入一个 ll 时，minl=lmin_l=l 处的标准和要增加 ll ，能与该点匹配的 cntcnt 不变，结果和要增加 l⋅cntll\cdot cnt_l；插入一个 xx 时，对于 minxmin_x 左侧的区间，标准和不变，能与区间中每处匹配的 cntcnt 增加 11，结果和要增加一个区间对应的标准和。
于是我们线段树中维护 std,cnt,sum,addstd,cnt,sum,add，分别为区间标准和，能与这段区间匹配的 xx 数量，区间结果和，（懒标记）区间加了多少次标准和，支持 stdstd 的单点加，cntcnt 的区间加，sumsum 的区间修改（cntcnt 及所谓区间加的定义其实并不严格，因为一段区间每个位置能匹配的 xx 的数量不尽相同，但由于 cntcnt 只在单点修改 ll 时由于需要补上之前加入的 xx 的贡献才使用，而一个单点能匹配的 xx 的数量是一定的，即 cntcnt 只需要下传，所以 cntcnt 才可以简单当作区间加处理定义是不知道该怎么描述）。
复杂度分析可以考虑点分治最坏情况下的形式就是一条链，形态类似线段树，相当于对线段树上每个点开一棵线段树，即树套树，故复杂度 O(nlog⁡2n)\mathcal{O}(n\log^2n) 。
一些实现细节：
  • 由于 (l,r,x)(l,r,x) 可以任意相等，所以可以作为 l,rl,r 的也可以作为 xx 。因此在同一高度的点的操作顺序应该是先插入 ll ，再插入 xx ，最后查询 rr 。
  • 子树去重时不能更新 minmin 和 maxmax ，仍然要保留原分治中心下的 minmin 和 maxmax 数值，否则起到的不是去重效果。
  • 对于每个分治中心需要离散化，不能直接扫描线 [1, n][1,~n] ，否则复杂度会退化至 O(n2log⁡2n)\mathcal{O}(n^2\log^2n) 。

cod.

CPP
#include <bits/stdc++.h>

#define file(name, suf) ""#name"."#suf""
#define input(name) freopen(file(name, in), "r", stdin)
#define output(name) freopen(file(name, out), "w", stdout)
#define map(type, x) static_cast<type>(x)

typedef unsigned int uint;

constexpr int N = 1e5 + 10;
int n, siz[N], son_siz[N], id[N], min[N], max[N];
std::vector<int> e[N], node;
bool arr[N];
uint ans;
struct Seg_Tree {
    struct Node { uint sum, std, cnt, add, clr; } t[N << 2];

#define ls (u << 1)
#define rs (u << 1 | 1)
#define mid ((l + r) >> 1)

    void up(int u) {
        t[u].sum = t[ls].sum + t[rs].sum;
        t[u].std = t[ls].std + t[rs].std;
    }

    void build(int u, int l, int r) {
        t[u] = {0, 0, 0, 0, false};
        if (l == r) return;
        build(ls, l, mid), build(rs, mid + 1, r);
    }

    void add(int u, uint x) { t[u].sum += t[u].std * x, t[u].cnt += x, t[u].add += x; }

    void down(int u) {
        if (t[u].add) add(ls, t[u].add), add(rs, t[u].add), t[u].add = 0;
    }

    void insert(int u, int l, int r, int k, uint x) {
        if (l == r) return t[u].std += x, t[u].sum += t[u].cnt * x, void();
        down(u);
        if (k <= mid) insert(ls, l, mid, k, x);
        else insert(rs, mid + 1, r, k, x);
        up(u);
    }

    void add(int u, int l, int r, int ql, int qr) {
        if (l > qr || r < ql) return;
        if (l >= ql && r <= qr) return add(u, 1);
        down(u), add(ls, l, mid, ql, qr), add(rs, mid + 1, r, ql, qr), up(u);
    }

    uint query(int u, int l, int r, int ql, int qr) {
        if (l > qr || r < ql) return 0;
        if (l >= ql && r <= qr) return t[u].sum;
        down(u);
        return query(ls, l, mid, ql, qr) + query(rs, mid + 1, r, ql, qr);
    }
} T;

int get_core(int u, int f, int all) {
    int core = son_siz[u] = (siz[u] = 1) - 1;
    for (const int& v : e[u])
        if (v != f && !arr[v]) {
            int res = get_core(v, u, all);
            siz[u] += siz[v], son_siz[u] = std::max(son_siz[u], siz[v]);
            core = !core || son_siz[res] < son_siz[core] ? res : core;
        }
    son_siz[u] = std::max(son_siz[u], all - siz[u]);
    return !core || son_siz[u] < son_siz[core] ? u : core;
}

void dfs(int u, int f) {
    node.push_back(u), siz[u] = 1, min[u] = std::min(min[f], u), max[u] = std::max(max[f], u);
    for (const int& v : e[u]) if (v != f && !arr[v]) dfs(v, u), siz[u] += siz[v];
}

void reput(int u, int f) {
    node.push_back(u);
    for (const int& v : e[u]) if (v != f && !arr[v]) dfs(v, u);
}

void erase(int u) {
    reput(u, 0), std::sort(node.begin(), node.end());
    int all = node.size();
    T.build(1, 1, all);
    for (const int& x : node) id[x] = std::lower_bound(node.begin(), node.end(), x) - node.begin() + 1;
    std::sort(node.begin(), node.end(), [](const int& a, const int& b) { return max[a] < max[b];});
    for (int i = 0, j; i < node.size(); i = j) {
        for (j = i; j < node.size() && max[node[j]] == max[node[i]]; j++) if (min[node[j]] == node[j]) T.insert(1, 1, all, id[node[j]], node[j]);
        for (j = i; j < node.size() && max[node[j]] == max[node[i]]; j++) T.add(1, 1, all, 1, id[min[node[j]]]);
        for (j = i; j < node.size() && max[node[j]] == max[node[i]]; j++) if (max[node[j]] == node[j]) ans -= T.query(1, 1, all, 1, id[min[node[j]]]) * node[j];
    }
}

void sol(int u) {
    arr[u] = true, dfs(u, 0);
    std::sort(node.begin(), node.end());
    int all = node.size();
    T.build(1, 1, all);
    for (const int& x : node) id[x] = std::lower_bound(node.begin(), node.end(), x) - node.begin() + 1;
    std::sort(node.begin(), node.end(), [](const int& a, const int& b) { return max[a] < max[b];});
    for (int i = 0, j; i < node.size(); i = j) {
        for (j = i; j < node.size() && max[node[j]] == max[node[i]]; j++) if (min[node[j]] == node[j]) T.insert(1, 1, all, id[node[j]], node[j]);
        for (j = i; j < node.size() && max[node[j]] == max[node[i]]; j++) T.add(1, 1, all, 1, id[min[node[j]]]);
        for (j = i; j < node.size() && max[node[j]] == max[node[i]]; j++) if (max[node[j]] == node[j]) ans += T.query(1, 1, all, 1, id[min[node[j]]]) * node[j];
    }
    for (const int& v : e[u]) if (!arr[v]) node.clear(), erase(v);
    node.clear();
    for (const int& v : e[u]) if (!arr[v]) sol(get_core(v, 0, siz[v]));
}

void solve() {
    std::cin >> n, max[0] = 0, min[0] = INT_MAX, ans = 0;
    for (int i = 1; i <= n; i++) e[i].clear(), arr[i] = false;
    for (int i = 1, u, v; i < n; i++) std::cin >> u >> v, e[u].push_back(v), e[v].push_back(u);
    sol(get_core(1, 0, n));
    std::cout << ans << "\n";
}

int main() {
    // input(main), output(main);
    int _ = 1;
    std::cin >> _;
    while (_--) solve();
    return 0;
}

评论

共 1 条评论，欢迎与作者交流。

正在加载评论...