一些好玩的经典游戏的数据

如果图片/链接炸掉，你可能要用和进入洛谷国际站相同的方法

本文大多数数字都要在前面加“约”。

石头剪刀布

规则

这是一个全球通用规则统一的双人零和博弈游戏。

有三个手势：石头（手捏券）、剪刀（食指和中指伸出）、布（手摊开），两个人各选一个手势

石头胜剪刀
剪刀胜布
布胜石头

如何玩这个游戏

先放统计

图片备用链接：https://cdn.luogu.com.cn/upload/image_hosting/yyh65pny.png

来源：[OC] Percentage of Americans who chose Rock, Paper or Scissors for each of the three rounds in the game.

可以看到，所有轮出石头的人都是最多的，第一轮占据了一半多！所以

如果对面是陌生人，第一轮出布的胜率是最高的，只有 $26\%$ 的概率输。
如果你认为对面知道这个东西且遇事只算期望的话就出石头
如果你觉得对面绝顶聪明：那就随便出吧，反正猜疑链下去都差不多

下几轮就太复杂了，不讨论。

生日悖论

介绍

只要有 23 个人，就有超过 50% 的概率至少有两个人同一天生日！

数据

您是 OIer，验证的话自己写一个期望 DP 算就行，就不放来源了。

人数 n	至少两人同一天生日的概率
$10$	$11.7\%$
$20$	$41.1\%$
$23$	$50.7\%$
$30$	$70.6\%$
$50$	$97.0\%$
$70$	$99.9\%$
$100$	$99.99997\%$
$366$	$100\%$

公式：

1 − (\frac{365!}{(365^n × (365−n)!)})

广义生日悖论

碰撞概率 $>50\%$	需要多少人
一年 $365$ 天	$23$ 人
$1\sim1000$ 的数字	$34$ 人
$1\sim10000$ 的数字	$118$ 人
任意哈希值（ $2^{256}$ ）	约 $2^{128}$ 人

这启示我们写双哈希。

猜数字

这个游戏并不出名，让我们先玩一遍这个游戏

规则

一个

10\sim50

的数字合法的要求这个数字十位和个位上的数都是偶数，且不能相同。

像

19,36

就不行。

现在你想一个合法的数字。

您心中的数字是（成功概率很低）

46

解释

猜完再看

这个游戏只有

30\%

的成功。

根据规则，可行的数只有：

CPP

20 24 26 28 40 42 46 48

这

8

个。然后在后面说了

像 $19,36$ 就不行。

这其实是暗示你往

>36

的数字想（不要问为什么，~~因为我也不会~~这是高深的心理学）

现在只剩下

40,42,46,48

了，

46

的概率最大。

数据：似乎没有，这个游戏是我在某本忘了的书上看到的，但和小学同学玩下来很对。

随机数字 1

规则

参加游戏首先需要上缴

100\times\mathsf{item.minecraft.nether\_star}

。

您首先选一个数字，然后在

1\sim100

中均匀随机选整数

10^{4}

次，统计这些数中和您选的相同的数字次数

\mathsf{cnt}

，您获得

\mathsf{cnt}\times\mathsf{item.minecraft.nether\_star}

。

显然的，这样无论怎么选择，最后期望都是

0

。

随机数字 2

规则

参加游戏首先需要上缴

120\times\mathsf{item.minecraft.nether\_star}

。

然后在

1\sim100

中均匀随机选整数

10^{4}

次，您在知道这些数据之后选择一个数，统计这些数中和您选的相同的数字次数

\mathsf{cnt}

，您获得

\mathsf{cnt}\times\mathsf{item.minecraft.nether\_star}

。

分析

这个游戏是赚的，纯数学证明比较困难，下面给出模拟的代码：

code with Github Copilot

CPP

#include <bits/stdc++.h>
using namespace std;

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    const int trials = 10000;      // 模拟次数，可自行调大
    const int draws = 10000;        // 每次抽样次数
    const int range = 100;          // 数字范围 1~100
    const int cost = 120;           // 入场费

    mt19937 rng(random_device{}());
    uniform_int_distribution<int> dist(0, range - 1);

    long long sum_max_cnt = 0;
    long long sum_profit = 0;
    int not_lose = 0;
    int win = 0;

    vector<int> cnt(range);

    for (int t = 0; t < trials; ++t) {
        fill(cnt.begin(), cnt.end(), 0);

        for (int i = 0; i < draws; ++i) {
            int x = dist(rng);
            cnt[x]++;
        }

        int mx = *max_element(cnt.begin(), cnt.end());
        sum_max_cnt += mx;

        int profit = mx - cost;
        sum_profit += profit;
        if (mx >= cost) not_lose++;
        if (mx > cost) win++;
    }

    cout << fixed << setprecision(6);
    cout << "Trials = " << trials << "\n";
    cout << "Expected max count = " 
         << (double)sum_max_cnt / trials << "\n";
    cout << "Expected net profit = "
         << (double)sum_profit / trials << "\n";
    cout << "P(not losing) = "
         << (double)not_lose / trials * 100 << "%\n";
    cout << "P(win) = "
         << (double)win / trials * 100 << "%\n";

    return 0;
}

通过模拟

10^5

次，得到赚的概率约为

91\%

，亏的概率约为

4.7\%

，期望是

126.013

，标准差

4.56

。

下面是表格：

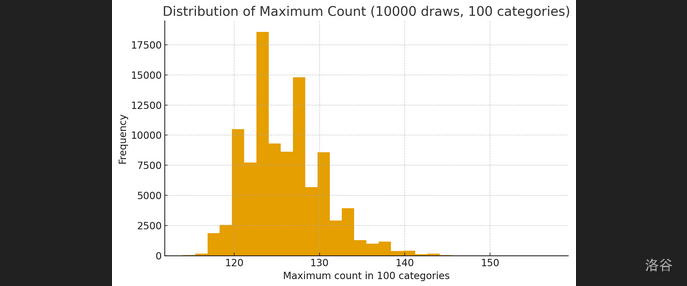
我也不知道为啥看起来比较神金。

AI 使用声明

这部分表格的绘制和模拟代码都有 AI 辅助（图片：GPT-5.1），已经审查内容保证无误。

随机数字 3

规则

参加游戏首先需要上缴

100\times\mathsf{item.minecraft.nether\_star}

。

您首先选一个数字，然后请一万名

{\color{red}\textup{\textmd{人类}}}

志愿者选择

1\sim100

的数字。统计这些数中和您选的相同的数字次数

\mathsf{cnt}

，您获得

\mathsf{cnt}\times\mathsf{item.minecraft.nether\_star}

。

分析

这个游戏看起来和第一个问题一样玩了个寂寞，但是您可以选择心理热门数字，下面放一个统计

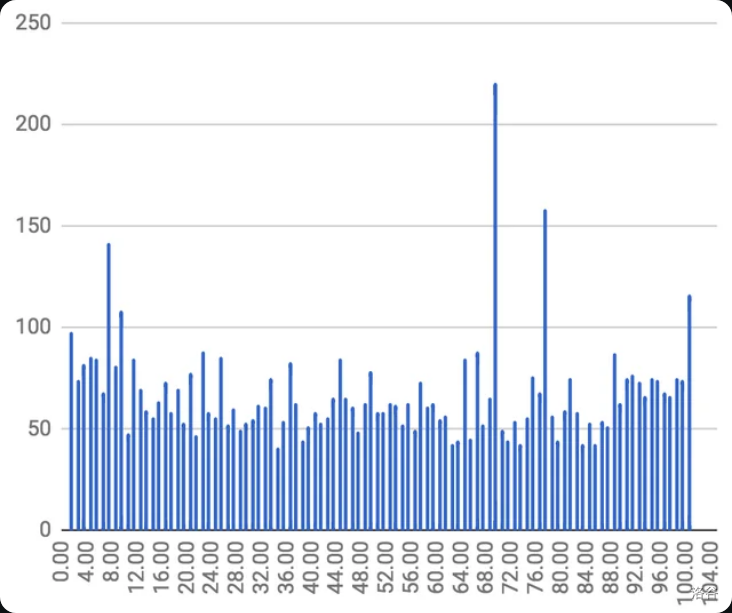
来源：Pick a number from 1-100: results from 6750 responses across various social media platforms [OC]

表格： https://docs.google.com/spreadsheets/d/1hG_25DCI2fMz210fCt84q-sVth3CNRBAT1OlT7zvKBk/edit?gid=1798635135#gid=1798635135

可以看到

69

这个数字在

6969

人随机选择下出现了

231

次！出现概率约

3.315\%

如果选择类似数字，是赚的。

一些好玩的经典游戏的数据

文章操作

石头剪刀布

规则

如何玩这个游戏

生日悖论

介绍

数据

广义生日悖论

猜数字

规则

解释

随机数字 1

规则

随机数字 2

规则

分析

随机数字 3

规则

分析

相关推荐

评论

一些好玩的经典游戏的数据