专栏文章

题解：AT_arc152_d [ARC152D] Halftree

hhxhhxh
AT_arc152_d题解参与者 2已保存评论 1

文章操作

快速查看文章及其快照的属性，并进行相关操作。

当前评论
1 条
当前快照
1 份
快照标识符
@mir023rt
此快照首次捕获于
2025/12/04 13:32
3 个月前
此快照最后确认于
2025/12/04 13:32
3 个月前
查看原文

题意

给定 n,kn,k，有一个 nn 个点的图，点编号为 0∼n−10\sim n-1.图初始为空，你需要做若干次操作，使得图变为一颗树，或说明无解。
操作：选择两个数 x,yx,y，连边 (x,y)(x,y)，((x+k) mod n,(y+k) mod n)((x+k)\bmod n,(y+k)\bmod n)。
1≤n≤2×1051\leq n\leq 2\times 10^5，1≤k<n1\leq k < n。

做法

nn 个点的数有 n−1n-1 条边，而操作每次都会加两条边，所以当 nn 为偶数时无解。下记 d=gcd⁡(n,k)d=\gcd(n,k)。
当 nn 为奇数时，考虑将 i→(i+k) mod ni\to (i+k)\bmod n 的边加在图上会发生什么。当 d=1d=1 时，裴蜀定理告诉我们所有点都在同一个环上；当 d>1d>1 时，+ k+\ k 对模 dd 的余数不会变，它会形成 dd 个环。
把他排得好看一点，比如像下面这样：
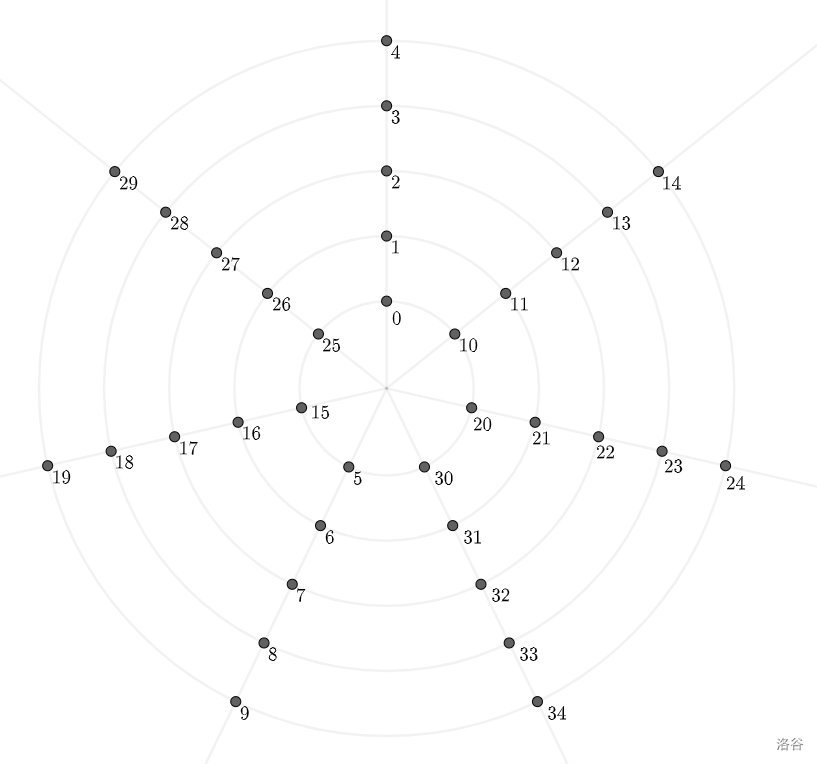
这是 n=35,k=10,d=5n=35,k=10,d=5 的情况。
首先，这样的图一定有奇数个环和奇数条射线（由于 nn）是奇数。在这样的图上，操作相当于连一条边，将它绕中心顺时针旋转 2dπn\frac{2d\pi}{n}，然后再连旋转后的边。下面把选的边 (x,y)(x,y) 标红，((x+k) mod n,(y+k) mod n)((x+k)\bmod n,(y+k)\bmod n) 标蓝。
先把大部分射线上的所有点连起来：
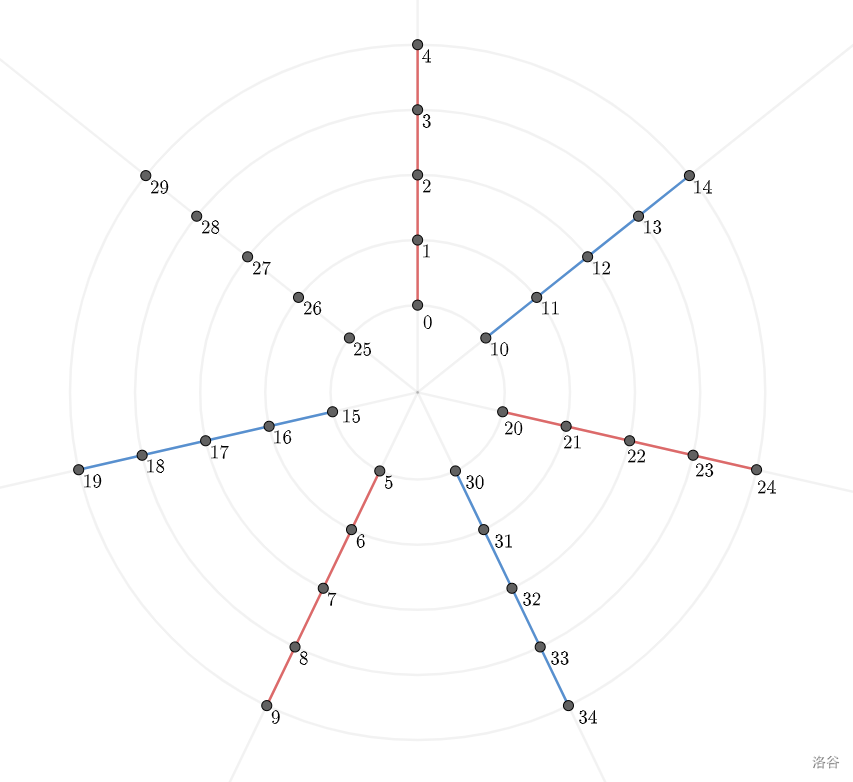
由于射线的个数是奇数，这样一定会剩下一条。考虑如何把这些链连起来：
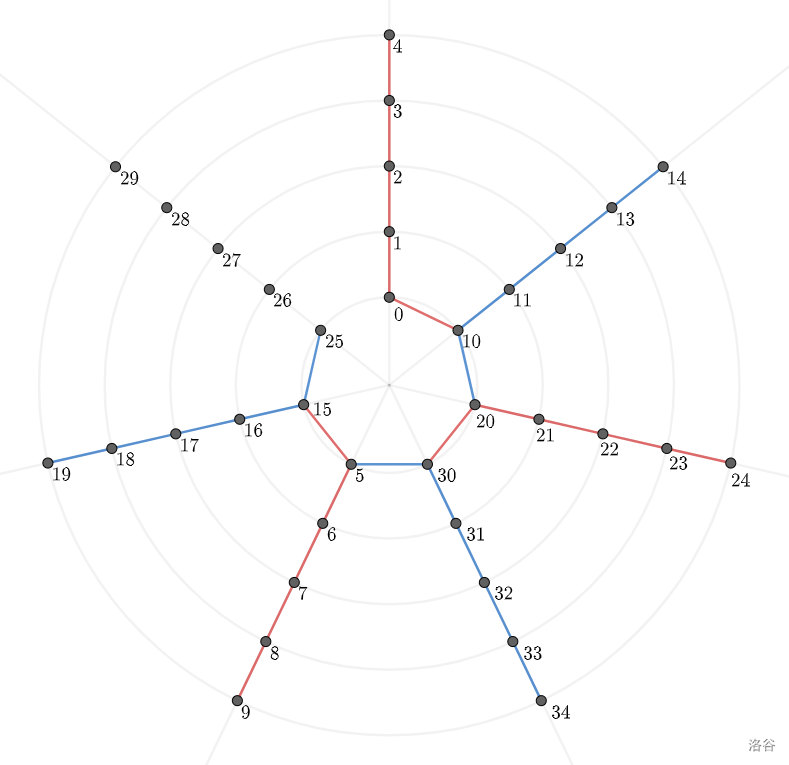
注意到，这里剩下的那一条射线的第一个点被我们接入树里了。接下来我们还剩偶数个点。像这样构造：
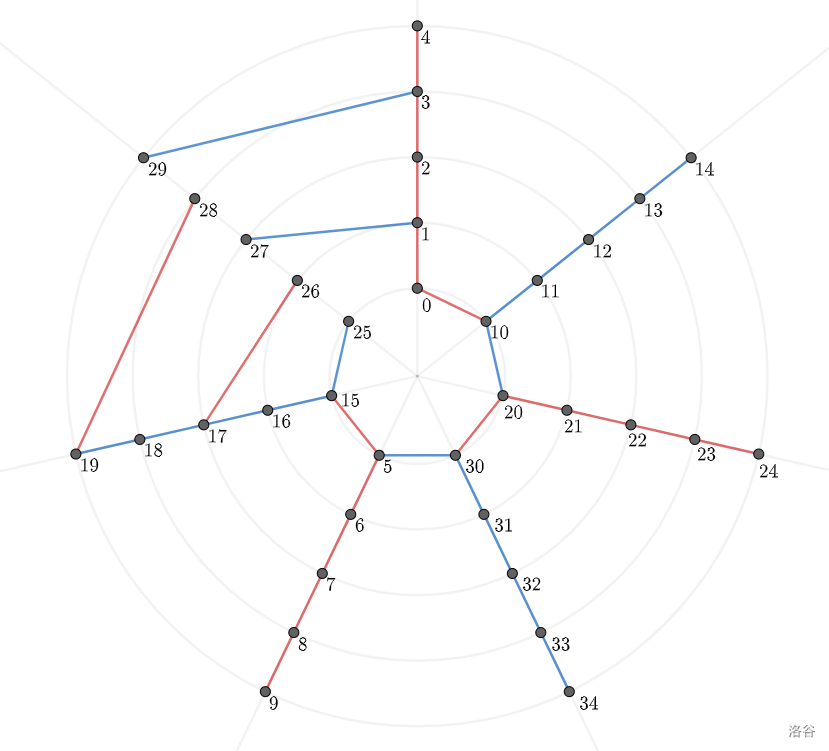
到这里我们就完成了 n=35,k=5n=35,k=5 的构造。把它加以推广就可以对于任何 n,kn,k 都构造出来了。

代码

CPP
#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,k,d;
vector<array<int,2> >p;
signed main(){
	cin>>n>>k;
	if(n%2==0) return puts("-1"),0;//唯一的无解情况
	d=__gcd(n,k);
	printf("%lld\n",n/2);
	auto add=[&](int x,int y){p.push_back({x,y});};//add(x,y)表示选择 (x,y)
	for(int j=0;j<n/d-1;j+=2) add(j*k%n,(j+n-1)*k%n);//第一个环
	for(int i=1;i<d;i++){
		for(int j=0;j<n/d-1;j+=2) add((j*k+i-1)%n,(j*k+i)%n);//连接第 i-1 个环和第 i 个环
		if(i&1) add((i-k-k+n+n)%n,(i-k+n+1)%n);//最后一步的构造
	}
	for(auto i:p) printf("%lld %lld\n",i[0],i[1]);
}

评论

共 1 条评论，欢迎与作者交流。

正在加载评论...