专栏文章

关于一道图论题&组合数学中的证

xxu_zhihao
算法·理论参与者 6已保存评论 6

文章操作

快速查看文章及其快照的属性，并进行相关操作。

当前评论
6 条
当前快照
2 份
快照标识符
@mklew7en
此快照首次捕获于
2026/01/20 01:01
上个月
此快照最后确认于
2026/02/19 01:16
13 小时前
查看原文

题目描述

将 nn 枚硬币任意摆放在图中的点上（每个点的硬币个数不限，可以为 00），对于图定义一次操作：从一个至少有 22 枚硬币的点取走 22 枚硬币，并分别在与此点相邻的点上各放置 11 枚硬币。对每种摆法，若点 EE 处无硬币，则总能经过若干次该操作使点 EE 处有硬币，求 nn 的最小值。

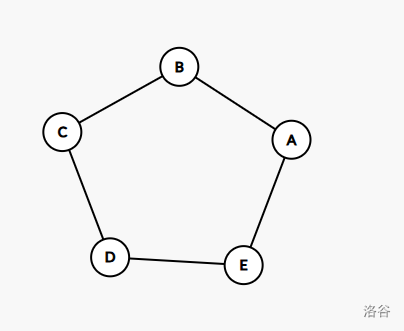
解法

定义环上两点的最短距离为在环上到达两点最少需要的步数，如 C,EC,E 两点的最短距离为 min⁡(2,3)=2\min(2,3)=2，A,BA,B 两点的最短距离为 min⁡(1,4)=1\min(1,4)=1。
定义环上两点的最长距离为在环上到达两点次少需要的步数，如 C,EC,E 两点的最长距离为 max⁡(2,3)=3\max(2,3)=3，A,BA,B 两点的最长距离为 max⁡(1,4)=4\max(1,4)=4。
定义合法为对于每种摆法，若点 EE 处无硬币，则总能经过若干次该操作使点 EE 处有硬币。
下述对于位置的描述默认不包括 EE。
首先，对于 n<5n < 5 的情况，显然根据鸽巢原理，在最坏摆法下，所有的位置最多都只有一个硬币。故 n<5n < 5 的情况不能满足对于每种摆法，能经过若干次该“操作”后使 EE 处有硬币。
对于 n=5n=5 的情况，对于每一种摆法，初始时都至少有一个位置的硬币数量大于等于 22，至多有两个位置的硬币数量大于等于 22，由于需要证明 n=5n=5 对于所有摆法都成立，所以根据有几个位置硬币的数量大于等于 22 进行分类讨论。
  • 前置性质：显然的，对于每一个位置上的点，到点 EE 的最短距离都小于等于 22。
  1. 初始时有一个位置的硬币数量大于等于 22。将这个位置记为 α\alpha。
    显然地，若 α\alpha 与 EE 相邻，那么对 α\alpha 进行一次操作后，点 EE 上就有了 11 枚硬币。所以下面的讨论都不包括 α\alpha 与 EE 相邻的情况。
    根据前置可知，若 α\alpha 上的硬币数量大于等于 44 的时候，对 α\alpha 进行 22 次操作，之后与其相邻的、在与 EE 的最短距离的路径上的点上的硬币数量至少为 22，可以对其进行 11 次操作，又因为前置性质，所以与此点相邻的点中必然有一个点为 EE。即操作结束后，EE 点必然有硬币。
    若 α\alpha 上的硬币数量等于 33 时，显然地，除了 α\alpha 外的其他位置上有且只有两个位置的硬币数量为 11。若在 α\alpha 与 EE 的最短距离的路径上的、与 α\alpha 相邻的点上有硬币（硬币数量为 11），那么对 α\alpha 进行 11 次操作后，此点上有 22 枚硬币，对其进行 11 次操作后，由于前置性质，所以与此点相邻的点中必然有一个点为 EE。即操作结束后，EE 点必然有硬币；若在 α\alpha 与 EE 的最短距离的路径上的、与其相邻的点上没有有硬币（硬币数量为 00），即在 α\alpha 与 EE 的最短距离的路径上的点上有且仅有 11 枚硬币（不包括点 EE 与点 α\alpha），这种情况和上面的情况相似，显然经过操作后 EE 点会出现硬币。
    若 α\alpha 上的硬币数量等于 22 时，显然地，除了点 E,αE,\alpha，其余的位置上有且仅有一枚硬币，对 α\alpha 进行一次操作，此时在 α\alpha 与 EE 的最短距离的路径上的、与 α\alpha 相邻的点上有 1+1=21+1=2 枚硬币，再将其进行一次操作，由于前置性质，所以与此点相邻的点中必然有一个点为 EE。即操作结束后，EE 点必然有硬币。
    综上所述，在初始时有一个位置的硬币数量大于等于 22 的情况下，是合法的。
  2. 初始时有两个位置的硬币数量大于等于 22。将两个位置分别记为 α,β\alpha,\beta。
    显然地，若 α\alpha 或 β\beta 与 EE 相邻，那么对 α\alpha 进行一次操作后，点 EE 上就有了 11 枚硬币。所以下面的讨论不包括 α\alpha 与 EE 相邻的情况。
    去除掉 α\alpha 或 β\beta 与 EE 相邻的情况后，只剩下 α,β\alpha,\beta 与 EE 的最短距离都为 22 的情况了，由于圆的对称性，所以对于 α,β\alpha,\beta 上硬币枚数颠倒的情况其实是和原来的情况一样的，故我们钦定 α\alpha 上的硬币数量小于等于 β\beta 上的硬币数量。
    对于 α,β\alpha,\beta 与 EE 的最短距离都为 22 的情况，显然地，α,β\alpha,\beta 相邻。若 α,β\alpha,\beta 上的硬币数量都为 22，那么对于除了 α,β,E\alpha,\beta,E 三点之外的两点中有 11 个位置上的硬币数量为 11，易证 α\alpha 或 β\beta 与这个位置与相邻，记与这个位置相邻的 α\alpha 或 β\beta 为 γ\gamma，那么对 γ\gamma 进行一次操作后，这个位置有 22 枚硬币，对这个位置进行操作，根据前置性质，所以与此点相邻的点中必然有一个点为 EE。即操作结束后，EE 点必然有硬币；若 α\alpha 上的硬币数量为 22，β\beta 上的硬币数量为 33，可以先对 α\alpha 进行一次操作，操作后 β\beta 上的硬币数量为 44，之后对 β\beta 进行两次操作后，在 α\alpha 与 EE 的最短距离的路径上的、与 α\alpha 相邻的点上有 22 枚硬币，最后将其进行 11 次操作，根据前置性质，所以与此点相邻的点中必然有一个点为 EE。即操作结束后，EE 点必然有硬币。
    综上所述，在初始时有两个位置的硬币数量大于等于 22 的情况下，是合法的。
由于对于两种可行可能都是合法的，所以当 n=5n=5 时，对于每种摆法，若点 EE 处无硬币，则总能经过若干次该操作使点 EE 处有硬币。
原命题得证，证毕。

进一步的推广

我们不难发现，对于一个有 mm 个点的环，都有一个最小值 n=mn=m（1<m1 < m ），且证法都形如上述证明。

评论

共 6 条评论，欢迎与作者交流。

正在加载评论...