2025.6.27 花了一上午增添了新内容，翻新了威佐夫博弈证明。大幅更新了自己理解下的 SG 函数，添加了自己 yy 的 trick。

2025.9.21 炸图紧急修复，Anti-Nim 结论错误紧急修复，灰常抱歉！

2025.11.18 NimK 结论反了紧急修复，感谢 mk14_61的指出。

2025.11.20 和 LCA 大佬讨论了一下，重写了部分内容，添加了新的例题，修改了例题部分。添加了关于 SG 函数求和的部分。

0. 前言

对于在信息学竞赛中的博弈论，我们研究的是组合博弈问题。

据不广泛观察显示，竞赛选手普遍的存在一种看见博弈论问题就会恐惧，这其实本质上源于博弈论问题往往综合了离散数学、组合游戏和算法多方面知识，非套路性较强。对状态空间的求解通常需要大胆的构造性证明或识别特定模式，而不是直接套模板。难以立即给出结论，必须反复试错、归纳证明。大佬们给出的参考是可以看作有交互性的构造题目。

所以在接下来的部分中，我们会介绍如下内容：

博弈论的基础知识：组合博弈与先后手。
博弈论的常见模型。
分析先后手决策的有力工具——SG 函数。
博弈论题目的常见解题方法。

下面进入正文环节。

1. 组合博弈与博弈基础

在信息学竞赛中，博弈题大多属于组合博弈问题即：

两名玩家轮流行动；
游戏状态和操作都是有限、可枚举的；
游戏没有随机因素，胜负完全由操作顺序和策略决定。

理解组合博弈，需要从以下几个基本概念入手。

1.1 公平组合与非公平组合

公平组合游戏：

由两名玩家交替行动；
任意一个游戏者在某一确定状态可以作出的决策集合只与当前的状态有关，而与游戏者无关；
游戏中的同一个状态不可能多次抵达，游戏以玩家无法行动为结束，且游戏一定会在有限步后以非平局结束。

例如取数游戏，Nim 游戏等，是公平组合游戏，我们下文会提到。

而非公平组合游戏，即在某一确定状态下作出的决策集合与游戏者有关，某一状态下，不同玩家可做的操作集合 可能不同。例如国际象棋，五子棋等是非公平组合游戏，因为双方不能使用对方的棋子。

以上是 Oi-Wiki 的内容，可能很抽象，但是提取重点的来说：

公平组合游戏：规则对每个人完全一样，没有人可以直接操作对手的资源。
非公平组合游戏：你能动的和对手能动的不一样，所以策略分析更复杂。

1.2 先手，后手，必胜必输局面

接下来我们定义几个名词：

局面：游戏进行中某一时刻的状态。
先手：整局游戏中第一个行动的玩家。
后手：整局游戏中第二个行动的玩家。

要注意局面的胜负属性总是相对于轮到谁行动而言。

这几个名词还是比较简单的。

必败局面：即玩家无论采取任何行动都无法胜利，都会输掉游戏。
必胜局面：即玩家在某一局面下存在至少一种行动，使得后手行动陷入必败局面。

注意其中名词加粗的部分。

1.3 先手必胜与先手必败

先手必胜状态： 先手行动以后，可以让剩余的状态变成必败状态 留给对手。(即可以走到某一个必败状态)
先手必败状态： 不管怎么操作，都达不到必败状态，换句话说，如果无论怎么行动都只能达到一个先手必胜状态留给对手，那么对手（后手）必胜，先手必败。（即走不到任何一个必败状态）

有如下定理：

没有后继状态的状态是必败状态。
一个状态是必胜状态当且仅当存在至少一个必败状态为它的后继状态。
一个状态是必败状态当且仅当它的所有后继状态均为必胜状态。

1.4 必胜点与必败点

必败点，又称

P

点，轮到行动的一方必败的局面，上一手必胜。。必胜点，又称

N

点，轮到行动的一方可以获胜的局面，有操作能进入

P

点。

所有终结点都是必败点。
从任何必胜点操作，至少存在一种方案可以进入必败点。
无论如何操作，必败点只能进入必胜点（不然先手怎么赢）。

1.5 小总结

组合博弈分析的核心是状态递推和先手后手决策。请务必先理解上述概念，在往下学习，打好基础最重要。

2. 基本公平组合游戏模型

本章将从最基础的公平组合游戏模型入手，介绍常见局面表示、操作集合、必胜/必败状态的递推规律。掌握这些模型，是应对大部分取石子类、堆叠类或分割类博弈题的基础。

2.1 Nim 游戏

给定 $n$ 堆物品，第 $i$ 堆物品有 $a_{i}$ 个。两名玩家分别行动，每次可以任选一堆，取出任意多个物品，可以一把取光但是不能不取。取走最后一个物品的人胜利。

~~Vim 游戏？~~

Nim 游戏没有平局，只有先手必胜和先手必败两种情况。我们有如下的判定定理来判定：

Nim 博弈先手必胜，当且仅当 $a_{1} \operatorname{xor} a_{2} \operatorname{xor} \dots \operatorname{xor} a_{n} \neq 0$ 。

其中

\operatorname{xor}

代表异或操作。

证明如下：

我们考虑，所有物品都被取光当然是一个必败局面（对手取走最后一件物品，已经取得胜利），此时

a_{1} \operatorname{xor} a_{2} \operatorname{xor} \dots \operatorname{xor} a_{n} = 0

。

对于一个局面如果

a_{1} \operatorname{xor} a_{2} \operatorname{xor} \dots \operatorname{xor} a_{n} \neq 0

，那么设

x

二进制表示下最高位的

1

在第

k

位，那么至少存在一堆物品使得它的第

k

位为

1

。显然

a_{i} \operatorname{xor} x < a_{i}

，我们就从

a_{i}

堆中取走若干物品，使其变为

a_{i} \operatorname{xor} x

，这个操作我们就是尝试将局面变为

a_{1} \operatorname{xor} a_{2} \operatorname{xor} \dots \operatorname{xor} a_{n} = 0

，容易证明这是最优策略。

对于任意一个局面，若

a_{1} \operatorname{xor} a_{2} \operatorname{xor} \dots \operatorname{xor} a_{n} = 0

，容易证明无论如何取物品，最后的局面异或起来都无法不等于

0

，那么综上所述

a_{1} \operatorname{xor} a_{2} \operatorname{xor} \dots \operatorname{xor} a_{n} \neq 0

，一定是必胜局面，一定存在一个情况让对手面临各堆物品异或起来为

0

的局面，证毕。

P2197 NIM游戏

CPP

#include<bits/stdc++.h>
using namespace std;
constexpr int MN=1e5+15;
int T,n;

int main(){
    cin>>T;
    while(T--){
        cin>>n;
        int ans=0;
        for(int i=1;i<=n;i++){
            int x;
            cin>>x;
            ans^=x;
        }
        if(ans) cout<<"Yes\n";
        else cout<<"No\n";
    }
    return 0;
}

2.2 Nim升级版——NimK

$n$ 堆石子，每次从不超过 $k$ 堆中取任意多个石子，取走最后一个物品的人胜利。

结论如下：

把

n

堆石子用二进制数表示，统计二进制数上

1

的个数，若每一位上

1

的个数

num_{1} \bmod (k+1)

全部为

0

，则先手必败，否则先手必胜。

证明还是类似于 Nim 游戏：

所有物品都被取光当然是一个必败局面，即全为 $0$ 。
任意一个先手必败状态，一次操作后必然会到达必胜状态（因为游戏是交替进行的。）在某一次移动中，至少有一堆被改变，也就是说至少有一个二进制位被改变。因为最多动 $k$ 堆，所以对于任意一个二进制位， $1$ 的个数最多改变 $k$ 。而由于原先的总数为 $k+1$ 的整数倍，那么改变后必然不可能是 $k+1$ 的整数倍。所以在必败状态下必然能转移到必胜状态。
而对于先手必胜，总有一种操作使其走到必败状态，即证明有一种方法让第 $i$ $i$ 位回到 $k+1$ $k + 1$ 的整数倍。有一个比较显然的性质，对于那些已经改变的 $m$ $m$ 堆，当前位可以自由选择 1 或 0。我们设除去已经更改的 $m$ $m$ 堆，剩下堆 $i$ $i$ 位上 $1$ $1$ 的总和为 $sum$ $s u m$ 。考虑分类讨论：
- $sum\le k-m$ ，此时我们可以将堆上的 $1$ 全部拿掉，让后让拿 $m$ 堆得 $i$ 位全部为 0。
- $sum>k-m$ ，此时我们在之前改变的 $m$ 堆中选择 $k+1-sum$ 堆，将他们的第 $i$ 位设置成 1。剩下的设置成 0。由于 $k+1-sum<k+1-(k-m)<m+1$ ,也就是说 $k+1-sum\le m$ ，故这是可以达到的。

故存在，证毕。

例题：SDOI2011黑白棋

2.3 阶梯 Nim 游戏

$n$ 堆石子，编号 1 到 $n$ 。初始第 $n$ 堆石子数为 $a_{i}$ ，保证单调不降。轮流取石子，每次从任意一堆拿走任意个，要求取完后每一堆剩余石子个数单调不降（没有石子的记为 0 个），先不能行动者败。

或者换一种表述：

有 $n$ 堆石子。除了第一堆外，每堆石子个数都不少于前一堆的石子个数。两人轮流操作。每次操作可以从一堆石子中移走任意多颗石子，但是要保证操作后仍然满足初始时的条件。没有石子可移动的人就输掉了游戏。

因为堆数是单调递增的，像一个阶梯，我们在阶梯取石子。所以叫阶梯 Nim 游戏。

结论：

阶梯 nim 的游戏结果与只看奇数堆的石子数的普通 nim 结果一致。

考虑证明：

首先末态一定是

a_{1} \operatorname{xor} a_{3} \operatorname{xor} a_{5}\dots=0

，那么如果初态

a_{1} \operatorname{xor} a_{3} \operatorname{xor} a_{5}\dots=0

，就一定存在一种方式将某奇数台阶的石子移动到偶数台阶上使得异或和为 0 。这样，不管后手的人是把奇数台阶的移动到偶数台阶还是相反，先手都一定存在一种方案使得异或和为 0 ,这样就一定能转移到末态，先手就赢了！

不太那么板题，需要一步转化：

P3480

CPP

#include<bits/stdc++.h>
using namespace std;
constexpr int MN=1520;
int T,n,a[MN],b[MN];

void solve(){
    cin>>n;
    int x=0;
    for(int i=1;i<=n;i++){
        cin>>a[i];
        b[i]=a[i]-a[i-1];
    }
    for(int i=n;i>=1;i-=2) x^=b[i];
    if(x) cout<<"TAK\n";
    else cout<<"NIE\n";
}

int main(){
    cin>>T;
    while(T--){
        solve();
    }
    return 0;
}

2.4 巴什博弈 Bash Game

~~Bash 命令行？~~

只有一堆石子，个数为 $n$ 个，两名玩家轮流在石子堆中拿石子，每次至少取 1 个，至多取 $m$ 个，最后一个取走石子的玩家为胜者。

结论如下：

若

(m+1)|n

，则先手必败，否则先手必胜。

证明如下：

当 $n\le m$ 时，显然先手必胜。
当 $n=m+1$ 时，先手最多取走 $m$ 个，无论取走多少个后手必胜。
若 $(m+1)|n$ ，假设先手拿走 $x$ 个，那么后手一定可以拿走 $(m+1)-x$ 个，这样无论怎么拿剩下的石头个数都是 $(m+1)$ 的倍数，那么最后一次取的石头一定还剩下 $m+1$ 个，显然必败。否则，先手取走模 $(m+1)$ 的手头，此时转化为 $(m+1)|n$ ，那么后手必败。

得证。

有板题：HDU4764

2.5 威佐夫博弈

有两堆石子，石子数可以不同。两人轮流取石子，每次可以在一堆中取，或者从两堆中取走相同个数的石子，数量不限，取走最后一个石头的人获胜。判定先手是否必胜。

同步发表于：P2252题解

威佐夫博弈不同于Nim游戏与巴什博奕，它的特殊之处在于不能将两堆石子分开分析。

证明可以不看的 www。

因为只有两堆石子，先进行一步转化给他丢到二维坐标系上，那么坐标

(x,y)

就表示两堆的石子数量。

我们考虑观察性质，我们可以枚举几个必败状态，例如 (0,0),(1,2),(3,5),(4,7)……

我们观察状态，可以发现两个规律，我们假设从小到大排的第

k

个必败状态是

(x,y)

，并且

x<y

。并且我们发现

y=x+k

。这个说明的就是必败状态两个数的差值是递增的，所以也就说明了每一个必败状态的差值都各不相同。证明我们待会在来看。

那么原来的问题，我们可以把游戏转化为，棋盘上有一个点，每个人可以将棋子往下，向左或向左下移动若干的棋子，不能移动的人。能够一步移动到原点的点显然就是必胜点，假设我们给这些所有必胜点都染色的话，剩下的的没当中横纵坐标和最小的点就是下一个必败点，因为无论如何移动都会给对手留下一个必胜点。

我们借用梁唐的知乎博客的图，将必败点染色可以得到如下图：

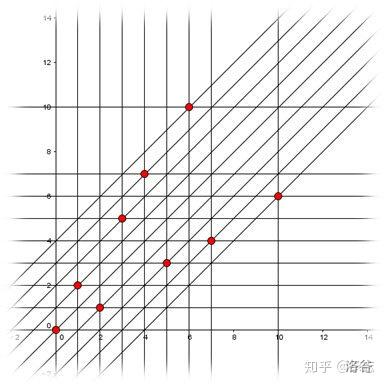
从图中不难看出，必败点之间是无法一次移动就能得到的，换句话说可以一次移动到必败点的点都是必胜点，那么上图中除了必败点之外的点都是必胜点，并且每一个自然数必然只会被包含在一个必败状态之中。

那么根据图的一些奇妙性质，我们定义，先手必输的局势为奇异局势。不妨设

(x,y)

为第

k

个奇异局势。那么有如下性质：

$x$ 为前 $k$ 个奇异局势中最小没有出现过的正整数， $y=x+k$ 。
任何一个自然数都包含在有且仅有一个奇异局势中。
任何操作都会将奇异局势变成非奇异局势。（必胜必然走向必败）
可以采取适当的方法让非奇异局势变成奇异局势。（即必败走向必胜点）

第一个，考虑反证法，假设

(a,a+k),(b,b+k)

是必败状态，并且

a<b

。那么先手面临

(b,b+k)

的时候，只需要在两堆当中同时取走

b-a

个石子，那么给后手的局面就是

(a,a+k)

。但是对于后手来说，这是一个必败的局面，那么

(b,b+k)

不就是必胜状态了吗，矛盾，所以不存在两个必败局面的差值相等。

第二个个证明考虑反证法，我们需要证明两点：

任意自然数都出现过。
任意自然数只出现一次。

证明如下：

反证法，如果 $v$ 没有出现过，那么 $v$ 显然可以做一个新奇异局势的 $x$ 。
反证法，假设 $v$ 出现了两次，那么 $v$ 一定不是所在奇异局势的 $x$ ，那么 $v$ 只能同时是两个奇异局势的 $y$ ，但因为任意一个奇异局势的差值不相同，所以 $v$ 不可能存在。

第三个，我们考虑若取走一堆中的石子，那么两对石子的差值会改变，必将成为非奇异局势。若同时取走，因为同一个差值只会对应一种奇异局势，必将成为非奇异局势。

第四个是显然的，不证明。

那么现在问题在于我们如何快速找出一个通项公式使得对于第

k

个必败局面，它的坐标是

(x_{k},y_{k})

呢？

我们有 Betty 定理！

设 $a,b$ 是两个正无理数，且 $\dfrac{1}{a}+\dfrac{1}{b}=1$ 。记 $P=\left\{ \lfloor a\times n \rfloor|n \in \mathbb{N}^{+} \right\},Q=\left\{ \lfloor b\times n \rfloor|n \in \mathbb{N}^{+} \right\}$ ，则 $P \cap Q=\varnothing,P \cup Q =\mathbb{N}^{+}$ 。

证明可以去网上看。

那不对啊，我们是自然数你这是无理数，你这八杆子打不着的东西拿出来用干啥啊。因为我们发现必败状态的通项和Betty定理序列很像。

我们不妨假设存在这样的

a,b

同时满足 Betty 定理和必败状态的性质，当然无理数不可能作为坐标出现啦，我们当然要让它变为整数。

那怎么办，Betty 有一个推论就是：

任何正整数都可刚好以一种形式表示为不大于其中一个无理数的正整数倍的最大整数。

从定理直接推，那么有如下式子：

\begin{cases} \lfloor a\times n\rfloor +n = \lfloor b\times n \rfloor \\ \frac{1}{a}+\frac{1}{b}=1 \end{cases}

解第一个方程：

\begin{aligned} \lfloor b\times n \rfloor & = \lfloor a\times n\rfloor +n \\ & = \lfloor a\times n +n \rfloor \\ & = \lfloor (a+1) \times n\rfloor \\ \therefore b &= a+1 \end{aligned}

那么代入第二个方程有：

\frac{1}{a}+\frac{1}{a+1}=1

开解！

\begin{aligned} & \frac{1}{a} + \frac{1}{a+1} = 1 \\ & \frac{1}{a} =\frac{a+1}{a(a+1)} \\ & \frac{1}{a+1} = \frac{a}{a(a+1)} \\ & \therefore \frac{a+1}{a(a+1)}+\frac{a}{a(a+1)}=1 \\ & \to \frac{2a+1}{a(a+1)}=1 \\ & \therefore 2a+1=a(a+1)=a^2 +a \\ & \therefore 2a+1-a^2 -a =0 \\ & \therefore a^2-a-1=0 \end{aligned}

利用初中知识不难得出

a=\dfrac{1+\sqrt{5}}{2}

或

\dfrac{1-\sqrt{5}}{2}

。

完了吗？敢说完了的扣 114514 分 (≧m≦)

设 $a,b$ 是两个正无理数，且 $\dfrac{1}{a}+\dfrac{1}{b}=1$ 。

正无理数！所以解为

a=\dfrac{1+\sqrt{5}}{2}

。

综上，假设两堆石子为

(x,y),x<y

。

那么先手必败，当且仅当：

(y-x) \times \frac{\sqrt{5}+1}{2}=x

其中，

\dfrac{\sqrt{5}+1}{2}

就是黄金分割数，很神奇的。

题目：P2252

CPP

#include<bits/stdc++.h>
#define double long long
using namespace std;
const double hjfg=((1.0+sqrt(5.0))/2.0);
double a,b;

int main(){
    cin>>a>>b;
    if(a>b) swap(a,b);
    double ans=(b-a)*((1.0+sqrtl(5.0))/2.0);
    if(ans==a) cout<<0;
    else cout<<1;
    return 0;
}

2.6 斐波那契博弈

有一堆个数为

n,(n\ge 2)

的石子，游戏双方轮流取石子，规则如下：

先手不能第一次全取完，至少取 $1$ 颗。
之后每次取的石子个数至少为 $1$ ，至多为对手所取的石子数的 $2$ 倍。

还是最后一个取走石子的为赢家。

先手必败，当且仅当石子数为斐波那契数

先证明必要性，斐波那契数一定先手必败，可以用数学归纳法，大致思路就是一定能拆成两堆斐波那契数，不论先手怎样取，后手总能取到最后一颗

然后证明充分性，由齐肯多夫定理定理：

任何正整数可以表示为若干个不连续的斐波那契数之和

那么这样就回到了斐波那契数列里，可以证明。

考虑最优决策：

若正整数 $n$ 不为斐波那契数，那么用上述定理表示后，最小的那一堆个数即为答案。

证明因为不存在相邻的斐波那契数，那么显然有

f_{j}>2 \times f_{i}

，只要我取第一个，那么对手一定取不完下一个，让后我捡漏，以此类推，一定能取道最后一个石子。

板题：P6847

CPP

#include<bits/stdc++.h>
#define int long long
using namespace std;

signed main(){
    int n;
    cin>>n;
    while(n){
        if(n==1){
            cout<<1;
            break;
        }
        if(n==2){
            cout<<2;
            break;
        }
        int a=1,b=2,c=3;
        while(c<n) a=b,b=c,c=a+b;
        if(c==n){
            cout<<n;
            break;
        }
        n-=b;
    }
    return 0;
}

3. SG与有向图游戏

3.1 有向图游戏

给定一个有向无环图，图中有一个唯一的起点，在起点上放有一枚棋子。两名玩家交替地把这枚棋子沿有向边进行移动，每次可以移动一步，无法移动者判负。该游戏被称为有向图游戏。

任何一个公平组合游戏都可以转化为有向图游戏。具体方法是，把每个局面看成图中的一个节点，并且从每个局面向沿着合法行动能够到达的下一个局面连有向边。转化为有向图游戏，也称绘制了它的博弈状态图（简称博弈图或游戏图）。

而对于有向图游戏中的每一个节点，都代表当前子游戏的状态。

3.2 Mex 运算

设

S

表示一个非负整数集合。定义

\operatorname{mex}(S)

为求出不属于集合S的最小非负整数的运算，即：

\operatorname{mex}(S)=\min \left\{ x \right\},x\in \mathbb{N},x\notin S

在代码中，可以用 set 或布尔数组记录出现过的 SG 值，快速求出 mex，有一些数据结构题目经常考察，但是这里是博弈论，我们不再过多涉及。

3.3 SG 函数

在有向图游戏中，对于每个节点

x

，设从

x

除法共有

k

条有向边，分别到达节点

y_{1},y_{2},\dots ,y_{k}

，定义

\operatorname{SG}(x)

表示为

x

的后继节点

y_{1},y_{2},\dots ,y_{k}

的

\operatorname{SG}

函数值所构成的集合再执行

\operatorname{mex}

运算的结果，即：

\operatorname{SG}(x)=\operatorname{mex}(\left\{ \operatorname{SG}(y_{1}),\operatorname{SG}(y_{2}),\dots,\operatorname{SG}(y_{k}) \right\})

特别的，整个有向图游戏

G

的

\operatorname{SG}

函数值定义为有向图起点

s

的

\operatorname{SG}

函数值，即

\operatorname{SG}(G)=\operatorname{SG}(s)

。

对于 SG 函数的定义有：

终止状态（无合法移动）： $\operatorname{SG}=0$ （必败点，P-position）。
非终止状态： $\operatorname{SG}(x)=\operatorname{mex}(\left\{ \operatorname{SG}(y_{1}),\operatorname{SG}(y_{2}),\dots,\operatorname{SG}(y_{k}) \right\})$ 。

SG 函数本质上可以看作对于当前局面的一种 压缩信息。

3.4 SG 函数与动态规划的关系

有向图游戏是 DAG，节点状态唯一，无后效性。

SG 函数递归求解与 DAG 上的动态规划等价，状态就是局面节点，而转移就是合法移动到后继节点，答案就是 SG 值。

3.5 SG 定理与组合游戏和

有向图游戏的和，即设

G_1,G_2,\dots,G_m

为若干子游戏，定义组合游戏

G=G_{1}+G_{2}+\dots+G_{m}

，规则为每次操作选择任意一个子游戏

G_{i}

并在上面行动一步。

其游戏

G

的

\operatorname{SG}

函数值等于它包含的各个子游戏

\operatorname{SG}

函数值的异或和，即：

\operatorname{SG}(G)= \operatorname{SG} (G_{1}) \operatorname{xor} \operatorname{SG} (G_{2})\operatorname{xor} \dots \operatorname{SG} (G_{m})

这里给出一个性质，由

\operatorname{mex}

得出某个状态的 SG 值一定在

O(\sqrt{m})

以内，其中

m

为有向图游戏的边数。

3.6 NIM 游戏与 SG 函数的结合

对于单堆的 Nim 游戏，我们很容易计算它的

\operatorname{SG}

值，设

\operatorname{SG}(m)

表示剩余

m

个式子状态的函数值，显然

\operatorname{SG}(0)=0

，那么以此类推，

\operatorname{SG}(1)=1,\operatorname{SG}(2)=2,\dots,\operatorname{SG}(n)=n

。因此，当石子数不为

0

时为必胜态。

而对于更多的，它们所有的堆都可以划分为一个单独的有向图游戏，而每一个有向图游戏的

\operatorname{SG}

函数值就是上面所以到的。那么，我们可以根据

\operatorname{SG}

定理，将它们给和起来，那么答案就是：

\begin{aligned} \operatorname{SG}(G) & =\operatorname{SG}(G_{1}) \operatorname{xor} \operatorname{SG}(G_{2)} \operatorname{xor} \dots \operatorname{xor} \operatorname{SG}(G_{n}) \\ & = a_{1} \operatorname{xor} a_{2} \operatorname{xor} \dots \operatorname{xor} a_{n} \end{aligned}

那么，我们就得到的 Nim 游戏的经典结论，是不是很神奇。

对于博弈的大部分问题，只要SG值相同，就可以互相转化，而对于 SG 函数来说，其求解依靠将一个总游戏划分成几个子游戏，简化问题逐个击破，通过定理就可以把他们的结果结合起来。

3.7 SG函数应用例题

然而问题在于，实际考察 SG 函数的题目其实只占到博弈论问题中的少数。是及其容易掰手指头算出来的。

在实际考虑博弈论问题中，SG 函数工具的使用可以将优先级放低一点。更应关注状态分析、最优策略构造等方面。

P1290

显然是公平组合游戏。

对于这种没有明显结论的博弈论题，我们先处理出特殊情况。

而对于本题来说，显然我们划分的子游戏就是每个人手里握的求。

我们考虑最终情况：一个数是

x

，而另一个是 0，那么先手必败（因为游戏已经结束了）。

剩下的情况就是握着两个数，不妨设为

x,y

，其中

x>y

。

那么根据题意有：

\operatorname{SG}(n,m)=\operatorname{mex}(\left\{ \operatorname{SG}(n-m,m),\operatorname{SG}(n-2m,m),\dots,\operatorname{SG}(m,n \bmod m) \right\})

考虑里面怎么求，注意到：

\operatorname{SG}(n-m,m)=\operatorname{mex}(\left\{ \operatorname{SG}(n-2m,m),\operatorname{SG}(n-3m,m),\dots,\operatorname{SG}(m,n \bmod m) \right\})

同理可以迭代下去，所以除了

\operatorname{SG}(m,n \bmod m)

以外其他都可以由他迭代出来，考虑如何求出来：

假设

\operatorname{SG}(m,n \bmod m)=0

，设

k=\dfrac{n}{m}

，那么有

\operatorname{SG}(n-(k-1)\times m,m)=\operatorname{mex}\left\{ \operatorname{SG}(m,n \bmod m) \right\}

成立。

假设

\operatorname{SG}(m,n \bmod m)=1

，那么

\operatorname{SG}(n-(k-1)\times m,m)=\operatorname{mex}\left\{ \operatorname{SG}(m,n \bmod m) \right\}

不成立。

由此可以看出，若

k=1,\operatorname{SG}(n,m)=[\operatorname{SG}(m,n \bmod m)=0]

，否则是 1。

一般来说，我们对于 SG 函数的求解，最常规的套路就是：暴力，找规律。或者打表。 大部分题都可以这么进行操作，有的时候需要进一步转化模型，当然那就是后面再说了。

这是标准的辗转相除的递推式子，用

\gcd

的写法即可实现：

CPP

#include<bits/stdc++.h>
using namespace std;
int T;

int dfs(int x,int y,int p){
    if(x==y) return p;
    if(y/x>=2) return p;
    return dfs(y-x,x,p^1);
}

void solve(){
    int m,n;
    cin>>m>>n;
    if(m>n) swap(m,n);
    if(dfs(m,n,0)==0) cout<<"Stan wins\n";
    else cout<<"Ollie wins\n";
}

int main(){
    cin>>T;
    while(T--){
        solve();
    }
    return 0;
}

P3179

对不起对不起忘放这个题了 (๑• . •๑)。

而本题，我们和上面，首先我们要分解出子游戏，这样我们才能利用 SG 函数求解。若我们无法分解为子游戏，我们需要考虑其他方法求解。

结论就是，每一个白色格子都是独立的，即一个白色格子处的决策与其他格子的状态无关，这样我们就划分出来子游戏了。

等等等等，你咋证明这个满足我们上面所说的有向图游戏的性质啊！

我们考虑，因为一个白格子可能会影响其他白格的情况，当且仅当这个白格翻转后有产生与其他白格重合的白格。这个时候我们应当把重合格子视为黑色格子，但是如果我们认为他们是两个独立的白格子，这显然是等价的，根据 SG 游戏和是异或的，异或和为 0，所以对这两个白色格子操作没有任何意义，得证。

感性理解就是一方操作了这两个白格中的一个，另一方可以立刻操作另一个，局势不发生变化。

我们对于翻棋子游戏，解法就是把初始状态的 SG 值即所有棋子的 SG 值异或和求出来，为 0 则必败否则必胜。

简单暴力，我们从后往前进行搜索，求出每一个白色格子出现在每一个位置的 SG 值，对于每一个白色格子，考虑枚举

k

的值，这个时候新状态的 SG 值是

\operatorname{SG}(x+ix)

，的异或和，其中

(1 \le i \le k-1)

。最后再求出所有转移到的状态 SG 值加上一个 0 的 mex。复杂度是

\sum\limits_{i=1}^n \lfloor \frac{n}{i} \rfloor =O(n \log n)

。

不难注意到是整除分块，考虑只维护

\lfloor \dfrac{n}{x} \rfloor

个不同的根号个

x

的 SG 函数，仍然按

x

从大到小考虑。对于每一个

x

考虑它的所有转移到的状态 SG 值仍然有如上性质，可以考虑

\lfloor \dfrac{n}{x} \rfloor

相同的一起计算，这是整除分块，时间复杂度是

O(n ^{\frac{3}{4}})

，可以通过。

CPP

#include<bits/stdc++.h>
using namespace std;
constexpr int MN=3e6+15;
int sg[2][MN],rt[MN],pos[MN],tot,n,n2,T;

inline int SG(int x)
{
	return ((x=n/(n/x))>n2)?sg[1][n/x]:sg[0][x];
}

void init(){
    for(int l=1,r;l<=n;l=r+1){
        r=n/(n/l);
        rt[++tot]=r;
    }
    ++tot;
    while(--tot){
        int x=rt[tot],y=0,z=1;
        pos[y]=tot;
        for(int i=x*2,j;i<=n;i=j+x){
            j=n/(n/i)/x*x,pos[y^SG(j)]=tot;
            ((j-i)/x&1^1)&&(y^=SG(j));
        }
        while(pos[z]==tot) ++z;
        (x>n2)?sg[1][n/x]=z:sg[0][x]=z;
    }
}

int main(){
    cin>>n>>T;
    while(n2*n2<=n) ++n2;
    n2--;
    init();
    while(T--){
        int w,x=0;
        cin>>w;
        for(int i=1;i<=w;i++){
            int awa;
            cin>>awa;
            x^=SG(awa);
        }
        cout<<(x?"Yes":"No")<<'\n';
    }

    return 0;
}

agc017d

还是我们的思路，分解子游戏。

首先源命题删边的操作，我们转化为删一个子树的操作（不能删整棵树），显然这个游戏是公平组合游戏，问我们初始状态，考虑利用 SG 函数求解。

首先，刻画游戏，我们终止状态是什么，显然当这个一个几点没有孩子节点的时候就是终止节点，那么 SG 函数为 0。

让后考虑我们怎么进行转移，还是上面我们所提到过的，对于这种没有明显结论的博弈论题，我们先处理出特殊情况。

$x$ 没有儿子，显然 SG 为 0。
$x$ $x$ 有一个儿子，设为 $y$ $y$ ，我们考虑证明 $\operatorname{SG}(x)=\operatorname{SG}(y)+1$ $SG (x) = SG (y) + 1$ 。
- 删除以 $y$ 为根的子树，显然 SG 为 0。
- 删除其他子树，显然这个子树在以 $y$ 为根的子树内，根据数学归纳法，SG 中 $0,1,\dots,\operatorname{SG}(y)-1$ 都出现了，则 $\operatorname{SG}(x)=\operatorname{mex}\left\{ 1,2,\dots,\operatorname{SG}(y) \right\}=\operatorname{SG}(y)+1$ 。
若 $x$ 有多个儿子，此时可以继续划分为好几个子游戏，根据 SG 定理结合起来即使答案。所以，SG 函数求解如下：

\begin{cases} 0 & \text{x has no son} \\ \\ \operatorname{xor}_{y\in son(x)} \operatorname{SG}(y)+1 & \text{otherwise} \end{cases}

时间复杂度

O(n)

。

CPP

#include<bits/stdc++.h>
#define int long long
using namespace std;
constexpr int MN=1e5+15;
int f[MN],n;
vector<int> adj[MN];

void dfs(int u,int pre){
    f[u]=0;
    for(auto v:adj[u]){
        if(v==pre) continue;
        dfs(v,u);
        f[u]^=f[v]+1;
    }
}

signed main(){
    cin>>n;
    for(int i=1;i<n;i++){
        int u,v;
        cin>>u>>v;
        adj[u].push_back(v);
        adj[v].push_back(u);
    }
    dfs(1,0);
    cout<<(f[1]?"Alice":"Bob");
    return 0;
}

P7864

同步发表于：题解

还是上面我们所提到过的，但是我们在增广一下，对于这种没有明显结论的博弈论题，我们先处理出特殊情况。在从特殊情况推广到一般情况。这也是大部分 OI 题的常规思路。

首先，树是一条链怎么做，经过手模显然在两端取，那么为偶数的时候先手必胜，反之为奇数的时候先手必败。

其次，我们考虑存在一个父节点，该节点存在多个叶子节点的形式，最经典的就是菊花图，那么有：

若只有一个叶子，显然先手必败。
若有多个叶子，那么先手可以把叶子节点拿到只剩下一个，那么就把必败的局面传给对方，因此先手必胜。

考虑推广一般情况，就是将根节点当成树的一部分结构，那么结构因为是公平组合游戏，那么一定是 P 点或者 N 点，若是 P 状态，我们直接把叶子节点全部拿完，如果是 N 状态，我们就只剩下一个叶子节点。

最后，我们推广到一般性情况。对于所有的第二种情况，先手都可以操纵，也就是说情况 2 是必胜态。如果否则一定存在若干个链条使得所有叶子节点都没有兄弟。这样的话我们需要判断的链条的长度，也就是从该叶子节点出发到达的第一个不是只有一个子节点的父节点，也就是直到一种情况 2 出现。因此我们计算出所有链条的长度，如果存在奇数，先手必胜；如果全是偶数，则后手必胜。

时间复杂度

O(n)

。

CPP

#include<bits/stdc++.h>
using namespace std;
constexpr int MN=1e6+15;
int T,n,fa[MN],dg[MN];

void clear(){
    for(int i=1;i<=n;i++) dg[i]=fa[i]=0;
}

void solve(){
    cin>>n;
    clear();
    for(int i=2;i<=n;i++){
        cin>>fa[i];
        dg[fa[i]]++;
    }
    for(int i=1;i<=n;i++){
        if(dg[i]) continue;
        int pre=fa[i],len=0;
        while(dg[pre]==1){
            pre=fa[pre];
            len++;
        }
        len++;
        if(len&1){
            cout<<1<<'\n';
            return;
        }
    }
    cout<<"0\n";
}

int main(){
    cin>>T;
    while(T--){
        solve();
    }
    return 0;
}

4. 反常游戏与反SG游戏

4.1 Anti-Nim游戏

是这样的：

有 $n$ 堆石子，两个人可以从任意一堆石子中拿任意多个石子(不能不拿)，拿走最后一个石子的人失败`。

不难发现和 Nim 游戏不同的一点就是胜利条件变了，不过条件还是可以推的。

先手必胜有两种情况：

对于每一堆都为 $1$ 个石子，只需要判断堆数的奇偶，奇数则先手必败，偶数则先手必胜。
至少一堆石子多于一个，且游戏的 $\operatorname{SG}$ 不为 0，即所有堆大小的异或和 $\neq 0$ 。

证明和 Nim 游戏是相似的，可以自行证明或网上搜索，这里就不给出了。

例题：SHOI2008 小约翰的游戏

CPP

#include<bits/stdc++.h>
using namespace std;
int T,n;

void solve(){
    cin>>n;
    int ans=0;
    bool flag=0;
    for(int i=1;i<=n;i++){
        int x;
        cin>>x;
        ans^=x;
        if(x>1) flag=1;
    }
    if(!flag&&!ans) cout<<"John\n";
    else if(flag&&ans) cout<<"John\n";
    else cout<<"Brother\n";
}

int main(){
    cin>>T;
    while(T--){
        solve();
    }
    return 0;
}

4.2 反 SG 游戏

我们根据 Anti-Nim 游戏能否推广到一般性情况呢？有的兄弟有的，反 SG 游戏就是。

我们定义：

Anti-SG游戏：在标准公平组合游戏基础上，将胜负条件反转——无法进行任何合法操作的玩家获胜（其余规则不变：两名玩家轮流行动、操作集合仅与状态有关、无环、有限步终止）。

那么，这种游戏还能用 SG 函数分析吗？显然就不太可以了，不过我们可以用 SJ 定理。

SJ 定理：

设一个 Anti-SG 游戏由 $m$ 个独立子游戏 $G_1,G_2,\dots,G_m$ 组成，记：

\operatorname{SG}(G) = \operatorname{SG}(G_1) \oplus \operatorname{SG}(G_2) \oplus \cdots \oplus \operatorname{SG}(G_m),

则先手必胜当且仅当满足以下两个条件之一：

$\operatorname{SG}(G) \ne 0$ ，且至少存在一个子游戏 $G_i$ 使得 $\operatorname{SG}(G_i) > 1$ ；

$\operatorname{SG}(G) = 0$ ，且所有子游戏的 SG 值均不超过 1（即 $\forall i,\ \operatorname{SG}(G_i) \in \{0,1\}$ ）。

在 Nim 中，单堆 SG 值就是石子数

a_i

：

若所有 $a_i = 1$ ，则所有 $\operatorname{SG} \le 1$ ，此时条件 (2) 生效：SG 总异或为 0（偶数堆）⇒ 先手必胜；
若存在 $a_i > 1$ ，则存在 $\operatorname{SG} > 1$ ，此时条件 (1) 生效：总异或 $\ne 0$ ⇒ 先手必胜。

注意游戏结束的唯一标准是：当前玩家没有任何合法移动。

和上面结论是一样的。

Anti-SG不怎么重要，我至今为止就做到过一道题

不过作为半家桶，还是要有这一部分的。

5. 常见解题方法

5.0 前言

文章最开头的前言提到，博弈论问题的本质可以看作构造体和交互题的结合，看似复杂，但大多数问题都可以通过系统化方法进行分析和求解。

博弈论题常用的解法套路包括：

SG 函数求解，博弈经典模型的套用。
不变量与决定量：检验石子总数、连通块数或其他图性质的奇偶性，迅速判断胜负点。
打表找规律：对于复杂状态难以推理的游戏，可编程打表寻找 SG 值规律，再用观察到的性质求解。
分类讨论：尝试分类讨论先手取值后手如何应对。如先手取最大、取最小或取0等不同策略对应对手的最优反应，从而分情形讨论最优值。
DP：用于有顺序依赖的取石游戏或游戏树上的取子游戏，状态可定义为当前位置及剩余限制，转移时考虑轮流性以及先后手选取情况。
贪心：当可将多个局合并为单一流程，可用贪心确定合并顺序。
对抗搜索：字面意义上的搜索先后手决策，需要一定的剪枝或其他优化。

遇到博弈题时首先寻求游戏的特殊性质（如可拆分子局、取法限制、对称性等），尝试分析所谓的最优策略是什么，构造简单策略；如果看不出规律，可尝试小规模模拟或打表，总结输赢条件。

5.1 例题

不保证题目难度严格递增。

ABC427_D

考虑 DP，设

f(i,j)

表示第

i

个点，现在是第

j

回合，Alice 是否能赢。有转移：

$j$ 为奇数，即 Alice 先手，则 $f(i,j)=\operatorname{OR}\limits_{v\in son(i)} f(v,j+1)$ 。
$j$ 为偶数，即 Bob 先手，则 $f(i,j)=\operatorname{AND}\limits_{v\in son(i)} f(v,j+1)$ 。

若

f(1,0)=0

则 Alice 先手必败，否则先手必赢，边界

f(i,2k)=[s_{i}=\texttt{A}]

，时间复杂度

O(k(n+m))

。

GZOI2017 取石子游戏

不难发现这是一个带特殊限制的 NIM 游戏。

让 Alice 必败就是让其选择的石子堆中的数量异或为 0，要么无法在这一堆中足够的石子使得剩下的异或为 0，所以给定 Alice 选择的石子数量一定要大于等于其他选择的堆的数异或值。

考虑枚举 Alice 选哪一堆，让后对于其他石子堆用 DP 求出前

i

堆中任意选择一些使得异或值为

j

的方案数，直接统计即可，时间复杂度

O(n^2 \times 256)

。

CPP

#include<bits/stdc++.h>
#define int long long
using namespace std;
constexpr int MN=520,MOD=1e9+7;
int f[MN][MN],ans,n,a[MN];

void solvedp(int x){
    memset(f,0,sizeof(f));
    f[0][0]=1;
    for(int i=1;i<=n;i++){
        for(int j=0;j<256;j++){
            if(i==x) f[i][j]=f[i-1][j];
            else f[i][j]=(f[i-1][j]+f[i-1][j^a[i]])%MOD;
        }
    }
}

signed main(){
    cin>>n;
    for(int i=1;i<=n;i++){
        cin>>a[i];
    }
    for(int i=1;i<=n;i++){
        solvedp(i);
        for(int j=a[i];j<256;j++){
            (ans+=f[n][j])%=MOD;
        }
    }
    cout<<ans;
    return 0;
}

神秘 OJ 题目。

有一列共 $n$ 道题目，第 $i$ 道题的难度系数为 $a_i$ 。现有两名玩家 Alice 和 Bob，他们轮流进行操作，且 Alice 先手。游戏规则如下：

每次操作，当前玩家会从剩余的题目中删除一定数量的题目（称为“切题”）。

Alice 在他的每个回合中必须切掉至少一道题（可以切多道）

Bob 在他的每个回合中必须且只能切掉恰好一道题。

当所有题目都被切完时，游戏结束。

每名玩家的得分为他切掉的所有题的难度系数之和。

在双方最优行动的前提下，Alice 最终能获得的最高得分是多少？ $1\le n \le 10^6,-10^9\le a_{i}\le 10^9$ 。

考虑 DP，最优决策下一定时从大到小拿取，证明考虑反证法与调整法证明即可，所以先排序，让后设

f(i,0/1)

表示到第

i

个题，当前是

\text{Alice}

先手还是

\text{Bob}

学长先手，

\text{Alice}

的最大得分。显然转移：

\begin{aligned} f(i,0)&=\max\limits_{j=1}^{i-1} f(j,1)+sum_{i}-sum_{j} \\ f(i,1)&=f(i-1,0) \end{aligned}

可以单调队列优化或线段树优化，时间复杂度

O(n \log n)

。

考虑分析策略，Bob 的策略总是选择当前剩余的最大数，Alice 只会在第一步选择超过一个数

将所有数字排序后 Alice 第一步一定选择一段前缀，枚举这个前缀，后面的部分是两个人轮流取最大数，这个过程可以前缀和优化快速计算。时间复杂度

O(n\log n)

。

USACO09NOV A Coin Game S

注意到是题目中的关键信息，取的硬币数和上一步取的操作有关，这个直接思考不太好，我们考虑进行 DP 求解。

设

f(i,j)

表示取到第

i

个金币，取金币的上限为

j

先手取的最大价值，转移是显然的，考虑记忆化搜索实现比较好些，但是转移是

O(n^3)

的。

考虑优化，注意到我们

f(i,j)

在记忆化搜索是

1 \rightarrow n

取搜索的，那么我们

f(i,j)

的答案其实包含了

f(i,j-1)

，那么我们可以直接搜

f(i,j-1)

没有的部分，即

(x+lim,lim\times 2)

，其中

lim

为金币上限，那么这样搜索复杂度就是

O(n^2)

的了。

CPP

#include<bits/stdc++.h>
using namespace std;
constexpr int MN=2e3+15;
int f[MN][MN],n,s[MN],c[MN];

int dfs(int x,int y){
    y=min(y,n-x+1);
    if(~f[x][y]) return f[x][y];
    if(x+y>n) return s[x];
    if(!y) return 0;
    int ans=dfs(x,y-1);
    ans=max(ans,s[x]-dfs(x+y,y<<1));
    return f[x][y]=ans;
}

signed main(){
    cin>>n;
    memset(f,-1,sizeof(f));
    for(int i=1;i<=n;i++){
        cin>>c[i];
    }
    for(int i=n;i>=1;i--) s[i]=s[i+1]+c[i];
    cout<<dfs(1,2);
    return 0;
}

AT_arc112_c [ARC112C]

感觉做这个题很好玩啊。

首先观察到一个性质就是如果

siz_{i}

为奇数那么先后手取的顺序就不一样了，否则还是原来那个顺序。所以对于一个点先手肯定优先走偶数保证自己占到主导权，并且肯定优先走

siz_{v}-f_{v}>f_{v}

的点，而对于

\le

的那些点走了获得负收益还不如走改变先后手的这样还容易有机会让后手吃诗。

那么奇数的怎么走？你发现走奇数会轮流改变奇偶性，如果每次双方都尽可能扩大自己的话那么最后相差没有太大变化，所以我们这个时候就要拉开差距，选择

siz_{v}-f_{v}-f_{v}

尽可能大的，这样我们就能先后手拉开差距。

当然啦，还要处理那些诗 qwq，记录一下奇数操作的先后手对应人，然后最后处理一下。时间复杂度

O(n\log n)\to O(n)

。

AT_arc105_e [ARC105E]

注意到末状态一定是两个完全图，其中一个属于一号点连通块，另一个属于

n

点连通块。设此时一号连通块大小为

siz_{1}

，那么此时双方累计删边为

\dfrac{n(n-1)}{2}-m-siz_{1}(n-siz_{1})

。当数量为奇数先手必胜，反之后手必胜。

注意到结果只和奇偶性有关，考虑从奇偶性入手，把前面的常数和符号去掉留下最后一个未知项，考虑分类讨论

siz_{1}(n-siz_{1})

的情况，发现其奇偶性和

n

有关，考虑分类讨论：

若 $n$ 为偶数：若 $siz_{1} \bmod 2=0$ ，那么后者 $n-siz_{1} \bmod 2=1$ 。反之同理故恒为偶数。
若 $n$ 为奇数，此时后者出现奇奇和偶偶配对。问题在于 $siz_{1}$ 的奇偶性，注意到合并奇数大小的连通块会改变奇偶性，而偶数大小不会。如果奇数大小连通块个数为偶数个，那么互相抵消答案取决于原图 $siz_1$ 奇偶性，反之为奇数个，则先手总可以保持 $siz_{1}$ 为奇数，并把剩余的丢到 $n$ 块中，故先手必胜。

时间复杂度

O(n)

。多过程的题目一定要考虑分析末状态的性质。

P8818 [CSP-S 2022] 策略游戏

这个特殊性质 A 可能看起来是送分，但是特殊性质 B 已经明显提示你该怎么做了。

没错，就是分类讨论，考虑特殊性质 B，那么我们考虑先手被固定的决策有：

先手取值为正数：后手取 $\min$ 。
先手取值为 $0$ ：答案固定，任意取值。
先手取值为负数：后手取 $\max$ 。

考虑后手固定的决策：

后手取值为正数：先手取 $\max$ 。
后手取值为 $0$ ：答案固定，任意取值。
后手取值为负数：先手取 $\min$ 。

到这里可以拿下

65

分，但是由于你了解先手与后手其中一个取值固定的决策。对于暴力你只枚举其中一个人的取值即可知道另一个人的取值，这个可以

O(qn\log n)

或

O(qn)

解决，拿下

85

分，还差最后一档分。

我们发现枚举取值显然是没太大前途，但是我们发现我们上面的取值只和正负性有关，考虑分类讨论我们区间内所包含正负数的情况，具体如下：

A 区间全为正数

(1) B 区间全为正数，A 取最大， B 取最小

(2) B 区间有正有负，A 取最小，B 取最小

(3) B 区间全为负数，A 取最小，B 取最小
A 区间有正有负

(1) B 区间全为正数，A 取最大，B 取最小

(2) B 区间有正有负，max(A 正数最小 × B 负数最小，A 负数最大 × B 正数最大)

(3) B 区间全为负数，A 取最小，B 取最大
A 区间全为负数

(1) B 区间全为正数，A 取最大，B 取最大

(2) B 区间有正有负，A 取最大，B 取最大

(3) B 区间全为负数，A 取最小，B 取最大

考虑

0

的情况，注意到

0

的作用只可能是保底，所以对 A 来说有

0

就是让他和答案取

\max

，而对

B

就是和答案取

\min

。

上面所有都是 RMQ 问题，可以用线段树或 ST 表维护，时间复杂度

O(q\log n)

。

AT_arc192_b [ARC192B]

我们考虑，如果只剩 1 堆没取，我们一定会去取这一堆。

然后还剩 2 对的话，这时的后手必胜。

显然，最后其他 n−2 堆一定会被取完。

然后，我们发现：先手想要到所有已被选的和为奇数，而后手想要为偶数。

然后我们就发现，我们只要记录可以改变奇偶的奇数的堆数就可以了。奇数个奇数先手赢，否则后手。

P4363

对于这种博弈论的题，基本上理解就能想到了把状态压出来，然后做记忆化搜索。

对于落子的限制条件是，上方和左方的格子要么是棋子要么是边界。

我们可以考虑直接状压落子的状态，存每一行铺到了哪个位置，这个方法的复杂度显然为

O(n^m)

的。

我们发现，一个棋子想要存在的条件是上方和左方的所有格子全部被棋子填满。

那么，对于任意时刻，棋盘上的棋子构成一个锯齿形。

那有用的情况有多少种呢，我们考虑从锯齿状的起点开始走，我们最多往右走

n

步，往下走

m

步，路径数论是多少？显然为

\dbinom{n+m}{n}

种。

算出来就是

184756

中，考虑暴力 11 进制状压，让后用 map 存就可以了。

注意开 long long。

CPP

#include<bits/stdc++.h>
#define int long long
using namespace std;
constexpr int MN=15,INF=1e18;
int a[MN][MN],b[MN][MN],ed,n,m;
map<int,int> ans,vis;

int dfs(int x,int y){
    if(x==ed) return 0;
    if(vis[x]==1) return ans[x];
    vis[x]=1;
    int p=1,sum=y?INF:-INF,tmp=x;
    int c[MN]{};
    c[0]=INF;
    for(int i=1;i<=n;i++) c[i]=tmp%11,tmp/=11;
    if(y){
        for(int i=1;i<=n;i++){
            if(c[i]<min(c[i-1],m)) sum=min(sum,dfs(x+p,y^1)-b[i][c[i]+1]);
            p*=11;
        }
    }
    else {
        for(int i=1;i<=n;i++){
            if(c[i]<min(c[i-1],m)) sum=max(sum,dfs(x+p,y^1)+a[i][c[i]+1]);
            p*=11;
        }
    }
    ans[x]=sum;
    return ans[x];
}

signed main(){
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            cin>>a[i][j];
        }
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            cin>>b[i][j];
        }
    }
    for(int i=1;i<=n;i++) ed=ed*11+m;
    cout<<dfs(0,0);
    return 0;
}

HNOI2010 取石头游戏

这种题的模型就是：“我可以死，但你要死的更惨！”。

由于得分之和是定值，且双方都想让自己分数最大，我们不妨令

val

表示先手得分与后手得分的差，类似于对抗搜索，那么先手要让

val

尽可能大，而后手尽量让

val

小。

而取石子，可以转化为两端分别有一个栈，可以从栈顶取石子，中间有若干个双端队列，可以从其两端取石子。

让后我们对连续的三个元素进行分类讨论，分别有：

递增
递减
先增后减
先减后增

因为我们取的方向是从外到内的，我们接下来分类讨论。

递增：我们肯定要放到后面选择，因为一旦先手选择，后手一定能够选择比他大的数的。
递减：优先选择递减里面最大的。
先增后减与先减后增：到了这个情况的化，后手肯定选择中间的情况，先手肯定会选择左后两个。考虑证明：
- 如果先手发现选取最优的话，他会选走这个。由于先增加后减少，所以当前对于后手而言，选取比上一次最优还优秀的点肯定是最佳的，随意肯定会选中间那个。
- 若不一定最优秀，那么可能会选取其他更优的决策点。但是最终还是要选择这个剩下的点。我们直接把这个情况压成一个点的情况，这样所有的双段队列和栈就不会出现任何线增加后减少的情况了。

贪心即可：

CPP

#include<bits/stdc++.h>

#define maxn 2000010
using namespace std;
typedef long long ll;
template < typename T > inline void read(T & x) {
    x = 0;
    char c = getchar();
    bool flag = false;
    while (!isdigit(c)) {
        if (c == '-') flag = true;
        c = getchar();
    }
    while (isdigit(c)) {
        x = (x << 1) + (x << 3) + (c ^ 48);
        c = getchar();
    }
    if (flag) x = -x;
}
ll n, sum, val, s, L, R, tot;
ll l[maxn], r[maxn], v[maxn];
bool tag[maxn];
bool cmp(const ll & a,
    const ll & b) {
    return a > b;
}
int main() {
    read(n), r[0] = 1, l[n + 1] = n;
    for (int i = 1; i <= n; ++i)
        read(v[i]), sum += v[i], l[i] = i - 1, r[i] = i + 1, tag[i] = (v[i] != 0);
    for (int i = 3; i <= n; i = r[i])
        while (tag[l[l[i]]] && tag[l[i]] && tag[i] && v[l[i]] >= v[l[l[i]]] && v[l[i]] >= v[i])
            v[i] = v[l[l[i]]] + v[i] - v[l[i]], r[l[l[l[i]]]] = i, l[i] = l[l[l[i]]];
    L = r[0], R = l[n + 1];
    while (v[L] >= v[r[L]] && tag[L] && tag[r[L]]) s += v[r[L]] - v[L], L = r[r[L]];
    while (v[R] >= v[l[R]] && tag[R] && tag[l[R]]) s += v[l[R]] - v[R], R = l[l[R]];
    for (int i = L; i <= R; i = r[i])
        if (tag[i])
            v[++tot] = v[i];
    sort(v + 1, v + tot + 1, cmp), v[++tot] = s;
    for (int i = 1; i <= tot; ++i) {
        if (i & 1) val += v[i];
        else val -= v[i];
    }
    printf("%lld %lld", (sum + val) / 2, (sum - val) / 2);
    return 0;
}

【集训队作业2018】三角形

绝好题，部分分导向设置完全合理，做出来的那一刻直接爽飞。

观察性质，不难发现一些性质：

只要父节点放了石子之后我们就可以立马撤销儿子节点的石子，这样操作一定是最优的。证明直接反证法即可。
根据上面的性质，可以推出局部最优解一定会导致全局最优解，因为每一层决策和儿子是有关的，直接贪心。

那么有一个想法就是自下而上维护石子的变化历史最大值，每个节点只考虑它的孩子的结果，然后直接得到自己的答案。对于历史最值显然我们有一个二元组维护的想法

(sum,hsum)

表示当前状态石子变化和历史石子和最值，显然有合并：

(x,y)+(x',y')\to (x+x',\max\{ y,x+y'\})

显然对于节点

i

的二元组（初始情况下）为

(w_{i}-\sum\limits_{v\in son(i)}w_{v},w_i)

，对于每一个节点我们让，但是我们显然不难发现一个问题在于每一层合并儿子的二元组的顺序不一样会导致答案的历史最值答案也是不一样的，如果暴力枚举合并的话时间复杂度是

O(n^2)

的。

接下来我们来看特殊性质，当

w

全部相同的时候怎么做，这个时候合并顺序就没有任何卵用了因为你怎么合并显然答案基本上都一致，甚至全局都是一致的。同时不难根据上面合并公式发现如果这个时候我们不考虑必须选儿子，直接任意合并都是可以的。

那么怎么做？贪心的想法就是让我们确定一个合并顺序，使得最终二元组历史最值最小，这就是经典的合并贪心问题（不会想二分吧？）。排序即可，二元组

x

，

y

顺序只要满足

(x+y)\to hsum < (y+x) \to hsum

即可把

x

放前面即可，时间复杂度

O(n\log n)

。

接着我们考虑有了儿子的限制怎么办，有个特殊性质就是

w_{i}\le w_{i+1}

，由于树编号满足小根堆性质显然直接按照顺序合并就可以了，没啥好说了。关键的来了，如果图是一个菊花图加延伸链怎么办？链的维护是显然的，但是问题在于根节点，处理根节点合并顺序是困难的。

我们考虑这个图可以看作一个内向树，即我们将依赖关系用有向边表示，发现最终都汇聚到根节点，既然各种各样的儿子我们不好维护，但是发现最终都汇聚到根节点。正难则反，考虑从根节点向下传递限制，那么操作将会翻转，即减少当前点的

w_{i}

，增加孩子的石子数。由于逆序操作和正序操作显然一一对应，同时一个点的二元组变为

(\sum\limits_{v\in son(i)}w_{v}-w_{i},\sum\limits_{v\in son(i)}w_{v})

，可以直接维护。

现在得到了一个经典问题，我们可以找到优先级最高的点

x

，如果

x

的父亲已经被加入，那么直接加入

x

；否则在

x

的父亲被加入时

x

会立刻被加入，这构成了一个依赖关系，把

x

和它的父亲合并即可。

由于子树内操作顺序不变，可以预处理出操作顺序。然后以操作顺序建立一棵线段树，通过线段树合并所提供的顺序得到答案，时间复杂度

O(n\log n)

。

6. 后言

博弈论在信息学竞赛中一直被视为“难点”，但更多时候，它难的不是知识本身，而是选手对博弈题的错误预期，容易被吓到。真正困难的不是博弈论，而是面对不确定性时的手足无措。但是有趣的也恰恰是，在先后手混乱中找出规律性，在对抗中建立秩序。

尝试分析性质，找出规律，简化问题，其实也是一般信息学竞赛题目的分析步骤。

希望读者能通过本博客得到一些博弈论题型的收获，不再被 “这是博弈题” 这几个字吓倒（就像题目开头第一句是本题是一道交互题一样），而是把它当作一道普通的逻辑题、一道需要分解和归纳的结构题。

祝好，也祝你在新的赛季中永远站在先手的一边。

修改了

+\infty

遍博客，耻辱求赞 QWQ，感谢大家的批评指出错误！也感谢 LCA 与星宇社的宣传本博客！

本文章好像拿下了 bing 搜索引擎关于：“博弈论 oi” 内容的极为靠前的排名，再次感谢大家的支持。

博弈论半家桶-从入门到门入从

文章操作

0. 前言

1. 组合博弈与博弈基础

1.1 公平组合与非公平组合

1.2 先手，后手，必胜必输局面

1.3 先手必胜与先手必败

1.4 必胜点与必败点

1.5 小总结

2. 基本公平组合游戏模型

2.1 Nim 游戏

2.2 Nim升级版——NimK

2.3 阶梯 Nim 游戏

2.4 巴什博弈 Bash Game

2.5 威佐夫博弈

2.6 斐波那契博弈

3. SG与有向图游戏

3.1 有向图游戏

3.2 Mex 运算

3.3 SG 函数

3.4 SG 函数与动态规划的关系

3.5 SG 定理与组合游戏和

3.6 NIM 游戏与 SG 函数的结合

3.7 SG函数应用例题

4. 反常游戏与反SG游戏

4.1 Anti-Nim游戏

4.2 反 SG 游戏

5. 常见解题方法

5.0 前言

5.1 例题

6. 后言

参考资料

相关推荐

评论

博弈论半家桶-从入门到门入从