专栏文章

题解：CF717F Heroes of Making Magic III

__2eyks
CF717F题解参与者 2已保存评论 1

文章操作

快速查看文章及其快照的属性，并进行相关操作。

当前评论
1 条
当前快照
1 份
快照标识符
@mimzozl6
此快照首次捕获于
2025/12/01 18:11
3 个月前
此快照最后确认于
2025/12/01 18:11
3 个月前
查看原文
思维好题，在 duel 的时候击杀了此题。
假设没有区间修改，只问一次是否可以击杀 [1,n][1,n] 内所有小怪。
容易发现“从区间一端走到另一端”完全可以变成从左边走到右边，因为路径是可逆的。
假定我们的路径出发点是 00（因为要先走到 11），终点是 nn。容易发现角色行走的路径是 S 形。我们可以把每次拐弯的点记录下来，这样，每段直走的路径，除了这段路径的出发点，每个位置都会打一次怪。
我们把这个对每段路径，做区间 +1+1 的操作改为在差分数组上处理，那么就会变成这样：
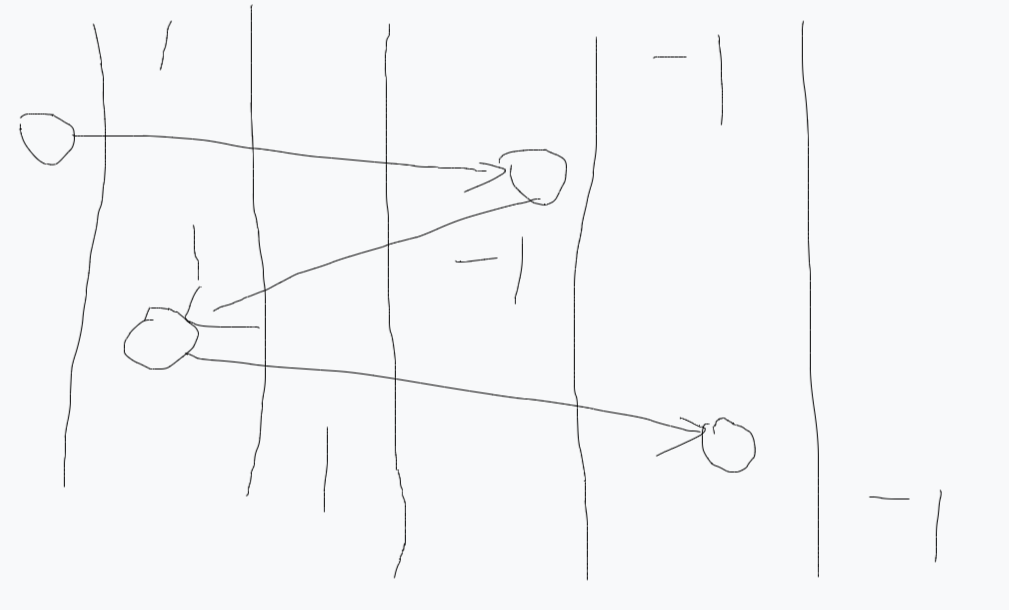
其中最左边是 00，最右边是 n+1n+1，图中是 n=4n=4，a={2,3,2,1}a=\{2,3,2,1\} 的一种合法路径。
容易发现：除了 11 位置会额外 +1+1，n+1n+1 位置额外 −1-1（不过 n+1n+1 位置在对差分做前缀和的时候一般是无效的），其余的都是形如对相邻两个位置 ±1\pm 1。
进一步发现，一组 +1+1 和一组 −1-1 是成对出现的，且 +1+1 的位置在 −1-1 之前。
我们考虑对于一个位置 ii，给 i,i+1i,i+1 位置 +1+1，给 i+1,i+2i+1,i+2 位置 −1-1，这样 i+1i+1 位置的操作抵消，就相当于可以给 i,i+2i,i+2 位置分别 +1,−1+1,-1。
所以问题变为：对 aa 求差分数组 bb，在将 b1b_1 减去额外 11 的贡献之后，能否通过给 i,i+2i,i+2 位置分别 +1,−1+1,-1 的操作，让 bb 变为全 00。
显然可以对位置的奇偶情况讨论，然后处理。
回到原问题，会发现线段树很好维护这些操作。特判 l=rl=r 即可。
CPP
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define fr first
#define sc second
#define pii pair<int,int>
#define yes cout<<"Yes\n"
#define no cout<<"No\n"
#define fo(i,l,r) for(int i=l;i<=r;i++)
#define ro(i,r,l) for(int i=r;i>=l;i--)
const int N=3e5+5;
int n,a[N],q;
namespace sgm{
    int m[2];
    struct sgm{
        #define lc (x<<1)
        #define rc (x<<1|1)
        #define mid ((l+r)>>1)
        int v[N],mn[N<<2],tag[N<<2];
        void build(int x,int l,int r){
            if (l==r){
                mn[x]=v[l];
                return;
            }
            build(lc,l,mid);
            build(rc,mid+1,r);
            mn[x]=min(mn[lc],mn[rc]);
        }
        void modify(int x,int l,int r,int ql,int qr,int k){
            if (ql<=l&&r<=qr){
                mn[x]+=k,tag[x]+=k;
                return;
            }
            mn[lc]+=tag[x],mn[rc]+=tag[x];
            tag[lc]+=tag[x],tag[rc]+=tag[x];
            tag[x]=0;
            if (ql<=mid)
                modify(lc,l,mid,ql,qr,k);
            if (qr>mid)
                modify(rc,mid+1,r,ql,qr,k);
            mn[x]=min(mn[lc],mn[rc]);
        }
        int query(int x,int l,int r,int ql,int qr){
            if (ql<=l&&r<=qr)
                return mn[x];
            mn[lc]+=tag[x],mn[rc]+=tag[x];
            tag[lc]+=tag[x],tag[rc]+=tag[x];
            tag[x]=0;
            int rt=1e18;
            if (ql<=mid)
                rt=min(rt,query(lc,l,mid,ql,qr));
            if (qr>mid)
                rt=min(rt,query(rc,mid+1,r,ql,qr));
            return rt;
        }
    }f[2];
}
using namespace sgm;
namespace bit{
    int c[N];
    void add(int x,int k){
        for (;x<=n;x+=(x&-x))
            c[x]+=k;
    }
    int query(int x){
        int rs=0;
        for (;x;x-=(x&-x))
            rs+=c[x];
        return rs;
    }
}
using namespace bit;
signed main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    cin>>n;
    fo(i,1,n)
        cin>>a[i];
    ro(i,n,1){
        a[i]-=a[i-1];
        add(i,a[i]);
    }
    fo(i,1,(n+1)/2){
        f[1].v[i]=a[i*2-1];
        f[1].v[i]+=f[1].v[i-1];
    }
    fo(i,1,n/2){
        f[0].v[i]=a[i*2];
        f[0].v[i]+=f[0].v[i-1];
    }
    m[0]=n/2,m[1]=(n+1)/2;
    f[0].build(1,1,m[0]);
    f[1].build(1,1,m[1]);
    cin>>q;
    while (q--){
        int op;
        cin>>op;
        if (op==1){
            int l,r,k;
            cin>>l>>r>>k;
            l++,r++;
            int l0=l,r0=r;
            l0+=(l0&1),r0-=(r0&1);
            l0/=2,r0/=2;
            int l1=l,r1=r;
            l1+=(l1&1^1),r1-=(r1&1^1);
            l1=(l1+1)/2,r1=(r1+1)/2;
            if (l&1)
                f[1].modify(1,1,m[1],l1,m[1],k);
            else f[0].modify(1,1,m[0],l0,m[0],k);
            if (r&1){
                if (r0<m[0])
                    f[0].modify(1,1,m[0],r0+1,m[0],-k);
            }
            else if (r1<m[1])
                f[1].modify(1,1,m[1],r1+1,m[1],-k);
            add(l,k),add(r+1,-k);
        }
        else{
            int l,r;
            cin>>l>>r;
            l++,r++;
            if (l==r){
                if (query(l)<=1)
                    cout<<"1\n";
                else cout<<"0\n";
                continue;
            }
            int l0=l,r0=r;
            l0+=(l0&1),r0-=(r0&1);
            l0/=2,r0/=2;
            int l1=l,r1=r;
            l1+=(l1&1^1),r1-=(r1&1^1);
            l1=(l1+1)/2,r1=(r1+1)/2;
            int lm0=0,lm1=0;
            if (l>1){
                if (l&1^1){
                    lm0-=f[1].query(1,1,m[1],l1-1,l1-1);
                    lm1+=f[1].query(1,1,m[1],l1-1,l1-1);
                }
                else{
                    lm0+=f[0].query(1,1,m[0],l0-1,l0-1);
                    lm1-=f[0].query(1,1,m[0],l0-1,l0-1);
                }
            }
            bool sb=1;
            sb&=(f[0].query(1,1,m[0],l0,r0)>=lm0+(l&1^1));
            sb&=(f[1].query(1,1,m[1],l1,r1)>=lm1+(l&1));
            if (r&1^1)
                sb&=(f[0].query(1,1,m[0],r0,r0)==lm0+(l&1^1));
            else sb&=(f[1].query(1,1,m[1],r1,r1)==lm1+(l&1));
            cout<<sb<<'\n';
        }
    }
    return 0;
}

评论

共 1 条评论，欢迎与作者交流。

正在加载评论...