题解：P14080 [GESP202509 八级] 最小生成树

题解

这里提供一种非常好写的做法——并查集。

遇到这种和最小生成树有关的题，一个基础的想法是先把不做修改的最小生成树求出来。然后发现只有在这个最小生成树上的边删掉才对答案有影响，不然就是原来的答案。

再看图：

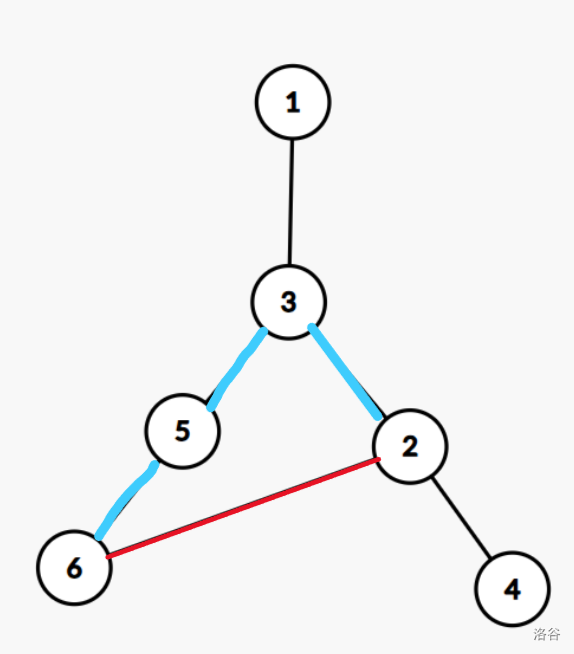
发现当我们把任意一条蓝色边删掉之后只要把红色边加上就可以让树重新联通，因为他们整体构成了一个环。

这时候我们再发现答案一定是把要删的边去掉再加一条边，即为原来的最小生成树边权和减去这条边的边权再加上新加的那条边。因为只要加一条边就能让两个联通块联通了。那么显然与自身无关的变量只有新加的那条边。

于是问题就变成了用非树边

(u,v)

覆盖树上路径

(u,v)

，并找到覆盖了每条边的边权最小的非树边。

直接树剖显然可以，但这里讲的是更好写的并查集。

首先发现，如果我们的非树边是按照边权升序排序的，那么每条树边的有效覆盖只有第一次，也就是说每条树边只会被覆盖一次。

于是直接用并查集暴力跳，每次把自己和父亲合并，直到两端点相会。具体实现上，我们只要把边挂在深度较大的点上就行，细节看代码。

总体来说还是很好写的。

AC_Code

CPP

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define PII pair<int, int>
#define xx first
#define yy second
const int N = 1e6 + 10;
int ww[N], n, m, fa[N], mi, dep[N], ans[N], f[N], re[N];
struct node{int u, v, w, id;};
vector<node> e, g;
vector<PII> G[N];
bool fl[N];
int find(int x){
	if(fa[x] != x)fa[x] = find(fa[x]);
	return fa[x];
}
void dfs(int x, int fa){
	f[x] = fa;
	dep[x] = dep[fa] + 1;
	for(auto i : G[x]){
		if(i.xx == fa)continue;
		re[i.yy] = i.xx;//映射一下是哪个点
		dfs(i.xx, x);
	}
}
signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0), cout.tie(0);
	cin >> n >> m;
	for(int i = 1; i <= n; i ++)fa[i] = i;
	for(int i = 1; i <= m; i ++){
		int u, v, w;
		cin >> u >> v >> w;
		ww[i] = w;
		e.push_back({u, v, w, i});
	}
	sort(e.begin(), e.end(), [](auto a, auto b){
		return a.w < b.w;
	});
	for(int i = 0; i < m; i ++){
		int x = find(e[i].u), y = find(e[i].v);
		if(x == y){
			g.push_back(e[i]);
			continue;
		}
		fl[e[i].id] = 1;
		G[e[i].u].push_back({e[i].v, e[i].id});
		G[e[i].v].push_back({e[i].u, e[i].id});//建树
		mi += e[i].w;//原来的答案
		fa[x] = y;
	}
	for(int i = 2; i <= n; i ++){
		if(find(i) != find(1)){
			for(int j = 1; j <= m; j ++)cout << -1 << '\n';//注意要输出m个，卡了我半天
			return 0;
		}
	}
	dfs(1, 0);
	for(int i = 1; i <= n; i ++)ans[i] = -1, fa[i] = i;
	for(auto i : g){
		int u = find(i.u), v = find(i.v), w = i.w;
		while(u != v){
			if(dep[u] < dep[v])swap(u, v);//跳深的
			ans[u] = w;//第一次覆盖更新答案
			fa[u] = find(f[u]);//合并
			u = find(u);//跳
		}
	}
	for(int i = 1; i <= m; i ++){
		if(fl[i]){
			if(ans[re[i]] == -1)cout << -1 << '\n';
			else cout << mi - ww[i] + ans[re[i]] << '\n';
		}else cout << mi << '\n';
	}
	return 0;
}

完结撒花。

题解：P14080 [GESP202509 八级] 最小生成树

文章操作

题解

AC_Code

相关推荐

评论

题解：P14080 [GESP202509 八级] 最小生成树