专栏文章

线段树究竟为何要开四倍空间，什么时候要？——严格数学推导证明

iicaijy
算法·理论参与者 3已保存评论 2

文章操作

快速查看文章及其快照的属性，并进行相关操作。

当前评论
2 条
当前快照
1 份
快照标识符
@mhz4uphg
此快照首次捕获于
2025/11/15 01:29
3 个月前
此快照最后确认于
2025/12/02 01:06
3 个月前
查看原文

引入

众所周知，假如我们建线段树是很传统的非叶节点 ii 有孩子 2i,2i+12i, 2i+1，则一般需要开 44 倍空间保险。所有人初学线段树时肯定都铭记了这一点。
但是仔细想想总感觉非常奇怪，到底什么时候真的会干到那么大呢？或者说，到底什么长度会导致需要四倍空间呢？所以今天我们来探讨下线段树占用空间的理论值。

暴力分析

首先我们定义一个函数 f(x)f(x)，表示通过如下方式建立的长度为 xx 的线段树，所占用的最大数组下标。
CPP
void build(int k,int l,int r)
{
	if(l==r)
	{
		//do something
		//e.g. tree[k]=a[l]
		return;
	}
	int mid=(l+r)>>1;
	build(k<<1,l,mid);
	build(k<<1|1,mid+1,r);
	//do something
	//e.g. tree[k]=tree[k<<1]+tree[k<<1|1]
}
例如 f(6)=13f(6)=13，代表长度为 66 的线段树，在数组存储中最大下标为 1313，如图所示：
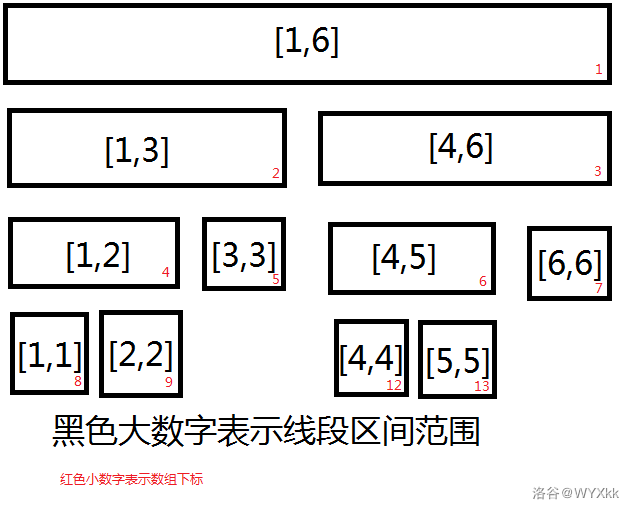
https://cdn.luogu.com.cn/upload/image_hosting/laie1is5.png
代码与图均来自 P6025，非常感谢此题提供的资源与帮助。
那么很显然我们可以写一个暴力枚举来计算 f(x)f(x)：
CPP
int f(int l,int r,int p=1){
    if (l==r) return p;
    int mid=(l+r)/2;
    return max(f(l,mid,p*2),f(mid+1,r,p*2+1));
}
思路就是每次出发取左右子树数组下标最大的那一个。
因为我们想要研究开几倍空间这个事，我们只关心 f(x)x\frac{f(x)}{x} 的值，写个代码看看是怎么个事：
CPP
#include <bits/stdc++.h>
#define int long long
using namespace std;

int f(int l,int r,int p=1){
    if (l==r) return p;
    int mid=(l+r)/2;
    return max(f(l,mid,p*2),f(mid+1,r,p*2+1));
}
signed main(){
    double maxn=0;
    for (int i=1;i<=10000;i++){
        int fx=f(1,i);
        cout<<"x: "<<i<<" f(x): "<<fx<<" f(x)/x: "<<(double)fx/(double)i<<endl;
        maxn=max(maxn,(double)fx/(double)i);
    }
    cout<<maxn;
}
输出为：
CPP
...
x: 9998 f(x): 32753 f(x)/x: 3.27596
x: 9999 f(x): 32753 f(x)/x: 3.27563
x: 10000 f(x): 32753 f(x)/x: 3.2753
3.93811
可以发现老祖宗的结论还是很正确的。大多数情况比值都在 33 以上，最坏的已经达到了 3.93.9 多了，看来开四倍空间还是非常有必要的。
但是，具体是为什么呢？有没有严格证明？

试图优化 f(x)

压下参数

我们发现，长度一样的子树建出来结构是一模一样的，与左右端点无关。因此我们可以把函数的 int l,int r 改成 int len，只关心长度即可。那么左右子树的长度就会变成 ⌊len+12⌋,⌊len2⌋\lfloor \frac{len+1}{2} \rfloor, \lfloor \frac{len}{2} \rfloor。因为显而易见的，在 lenlen 为偶数时两子树长度相同，否则左子树会长 11。
CPP
int f(int len,int p=1){
    if (len==1) return p;
    return max(f((len+1)/2,p*2),f(len/2,p*2+1));
}

优化成 O(log⁡2(n))O(\log_2(n))

如果自己多画几个图，或者稍微动脑筋想一想，就会发现大多数情况下，占用最大下标的那个节点会出现在右子树。毕竟右边可是 2i+12i+1 嘛，比左子树会大点。
但是仍然有某些情况它在左子树，比如 33 就是。
CPP
[1,2,3]
[1,2],[3]
[1],[2]
那么什么时候会取左子树呢？如上文所述，左子树在长度为奇数时会长 11，正是因为这个特性导致我们可能会选左子树。
结论是：当长度为 2k+1+1,k∈Z+2^{k+1}+1, k \in \mathbb{Z}^+ 时我们需要取左子树。这个数在二进制下为形如 1000…00011000\dots0001 这样的数，所以下文的讨论将更多在二进制下进行。
证明也非常好理解。当两个子树深度相同的时候我们肯定会取右子树。但当右子树已经是满二叉树了，没地了，这时假如我们把长度加 11，这就会导致左子树长度加 11，原本左子树是满二叉树，现在长度变长了，自然深度就变深了，就需要取左子树了。
所以我们代码可以优化成每次自己手动选择左子树右子树，且只用选一个：
CPP
int f(int len,int p=1){
    if (len==1) return p;
    if (len&1&&!((len-1)&(len-2))) return f((len+1)/2,p*2);
    return f(len/2,p*2+1);
}

优化成 O(1)O(1) 数学公式

有没有办法可以把上述的过程通过公式模拟出来呢？我们先看一个计算的例子（来源：CDFLS_mao_zx的P6025题解）：
CPP
当前节点下标=00000001 当前长度=1001011
当前节点下标=00000011 当前长度=0100101
当前节点下标=00000111 当前长度=0010010
当前节点下标=00001111 当前长度=0001001
当前节点下标=00011110 当前长度=0000101
当前节点下标=00111100 当前长度=0000011
当前节点下标=01111000 当前长度=0000010
当前节点下标=11110001 当前长度=0000001
我们发现，f(x)f(x) 的值仅与 xx 在二进制下最高位与次高位有关！
注意一下，当 x=2k+1,k∈Zx=2^{k+1}, k \in \mathbb{Z} 时，不存在次高位的 11，应当特判返回 2x−12x-1（此时是满二叉树）。接下来分析认为 xx 至少包含两个二进制下的 11
其实很好理解。我们模拟下我们是怎么取的：
  1. 当前 len 是 11，即叶节点时，直接返回。
  2. 当前 len 不是 2k+1+1,k∈Z+2^{k+1}+1, k \in \mathbb{Z}^+，那么就一直取右节点。这个时候会将当前下标左移一位并且加一。len 会右移一位
  3. 否则我们的 1en 在二进制下就是 100…0001100\dots0001 这样的数。这个时候相当于左子树在原本满二叉树的情况下加了一。这样我们就会一直选左子树，直到儿子为叶节点。此时下标会左移一位。len 会右移一位并且加一。加一是因为此时长度肯定为奇数。
所以最终得出了一个形如 1111…11000…00011111\dots11000\dots0001 这样的数。
假设 h1,h2h_1,h_2 分别代表最高位与次高位的数。则： f(h1,h2)=111…1⏟h2 个 1000…0⏟h1−h2 个 01f(h1,h2) = {\underbrace{111\dots1}_{h_2\text{ 个 }1}}{\underbrace{000\dots0}_{h_1-h_2\text{ 个 }0}}{1}
这个时候我们就得出了一个 O(1)O(1) 的公式来求解啦！
CPP
int f(int x){
    int h1=__lg(x);
    if (x==1ll<<h1) return 2*x-1;
    x^=1ll<<h1;
    int h2=__lg(x);
    return ((1ll<<h2+1)-1)<<(h1-h2+1)|1;
}
注意，此时用了不少位运算的技巧，不理解也没问题，只需要知道它模拟了上述公式即可。

数学推导证明

那么把这个函数翻译成数学语言，则是： x=2h1+2h2+c,0≤c<2h2,h1>h2x = 2^{h_1} + 2^{h_2} + c, \quad 0 \le c < 2^{h_2}, h_1 > h_2 f(x)=(2h2+1−1)⋅2h1−h2+1+1f(x) = (2^{h_2+1}-1) \cdot 2^{h_1-h_2+1} + 1
太完美了！那么接下来我们要看开多少倍空间的最坏情况，只需要求 f(x)x\frac{f(x)}{x} 的最大值即可。 已知 cc 不会影响 f(x)f(x) 所以如果我们希望 xx 尽可能小，则 c=0c=0。 所以，我们只需要研究： (2h2+1−1)⋅2h1−h2+1+12h1+2h2\frac{(2^{h_2+1}-1) \cdot 2^{h_1-h_2+1}+1}{2^{h_1}+2^{h_2}} 的最大值即可。把 h2h_2 当作是变量，h1h_1 当作是常量： g(h2)=(2h2+1−1)⋅2h1−h2+1+12h1+2h2g(h_2)=\frac{(2^{h_2+1}-1) \cdot 2^{h_1-h_2+1}+1}{2^{h_1}+2^{h_2}}
这里我使用 desmos 画下函数图，发现它好像是一个单峰的，导数单调递减的图。我们希望通过这些性质推一下在什么情况下 g(h2)g(h_2) 会取到最大值，这个最大值是多少。
先说结论：
  1. g(x)g(x) 在 h2=⌊h1−22⌋h_2=\lfloor\frac{h_1-2}{2}\rfloor 的时候取到最大值。
  2. lim⁡h1→∞g(⌊h1−22⌋)=4\lim\limits_{h1\to\infty}{g(\lfloor\frac{h_1-2}{2}\rfloor})=4，所以最坏时确实需要开 44 倍空间。

严谨证明

令 A=2h1>0, B=2h2>0,A=2^{h_1}>0,\ B=2^{h_2}>0,，则： g(h2)=4A−2AB+1A+Bg(h_2)=\frac{4A-\frac{2A}{B}+1}{A+B}

单峰性

对 BB 求导： h′(B)=2A2−4AB2+4AB−B2(A+B)2B.h'(B)=\frac{2A^2-4AB^2+4AB-B^2}{(A+B)^2B}. 当它为 00 时即为函数顶点。此时我们只关心分子即可，稍微整理一下得： (4A+1)B2−4AB−2A2=0.(4A+1)B^2-4AB-2A^2=0. 该方程在 B>0B>0 上仅有一个根： B∗=A(2+8A+6)4A+1B^*=\frac{A(2+\sqrt{8A+6})}{4A+1}
且导数符号由正变负，故 g(B)g(B) 仅有一个极大点，可以证明函数为单峰函数，且只有一个最大值。最大值左边单调递增右边单调递减。

极大点位置

知道这个函数的形状如此完美后，我们来推一推整数的情况下这个最大值取在哪。考虑一个差分函数： △(B)=g(h2+1)−g(h2)\triangle(B)=g(h_2+1)-g(h_2) 若 kk 为最后一个符合 △(k)>0\triangle(k)>0，最终取到最值的则是 k+1k+1。
通过比较繁琐的计算后我们可以发现 △(B)\triangle(B) 的分母恒正，分子为 −(4A+1)B2+3AB+A2-(4A+1)B^2+3AB+A^2。好消息是这仍然是一个二次函数，它的正根为： R=A(3+16A+13)2(4A+1)R=\frac{A(3+\sqrt{16A+13})}{2(4A+1)} 我们有 2h2−1<R<2h22^{h_2-1}<R<2^{h_2}。所以，最终的 h2h_2 即为 ⌈log⁡2R⌉\lceil\log_2R\rceil。 这里通过估算下 RR 中各个元素上下界，省略掉一些常数可以计算出 RR 的范围是： 2h12−1<R<2h122^{\frac{h_1}{2}-1}<R<2^\frac{h_1}{2} 因此，h2>h1/2−1h_2>h_1/2-1，所以在 h1h_1 为偶数时 h2=⌊h12⌋h_2=\lfloor\frac{h_1}{2}\rfloor 时取到最大值。
对于奇数的 h1h_1，我们设 h1=2m+1h_1=2m+1，将其代入后，使用同样的方法估算上界，可以证明 R<2m=2⌊h12⌋R<2^m=2^{\lfloor\frac{h1}{2}\rfloor}。最终结论与偶数相同，h2=⌊h12⌋h_2=\lfloor\frac{h_1}{2}\rfloor 时取到最大值。

最大值与上界

最后，我们就可以算一下最坏情况下是多少倍了。即求： lim⁡h1→∞g(⌊h12⌋)\lim\limits_{h1\to\infty}{g(\lfloor\frac{h_1}{2}\rfloor)} 已知： g(h2)=4A−2AB+1A+Bg(h_2)=\frac{4A-\frac{2A}{B}+1}{A+B} 我们变形一下，上下同时除以 AA，既有： g(h2)=4−2B+1A1+BAg(h_2)=\frac{4-\frac{2}{B}+\frac{1}{A}}{1+\frac{B}{A}} 在极限的运算下，所有分母为 AA 的数都无限趋近于 00，因此我们有： lim⁡h1→∞g(h2)=4−2B\lim\limits_{h1\to\infty}{g(h_2)}=4-\frac{2}{B} 因为 h2=⌊h12⌋h_2=\lfloor\frac{h_1}{2}\rfloor，所以 h2h_2 也趋近于无穷，因此便证明了极限趋近于 44。

例子

整了半天，那么到底什么时候空间浪费的比较多，比较靠近四倍空间呢？如果我们需要一个例子，只需要指定一个 h1h_1，然后算出 h2=⌊h12⌋h_2=\lfloor\frac{h1}{2}\rfloor，最后算出原始的长度 x=2h1+2h2x=2^{h_1}+2^{h_2} 即可，且 h1h_1 越大最终就越趋近于 44。
比如，指定 h1=30h_1=30，我们模拟一下：
CPP
#include <bits/stdc++.h>
using namespace std;
#define int long long
int calc(int x){
    int h1=__lg(x);
    if (x==1ll<<h1) return 2*x-1;
    x^=1ll<<h1;
    int h2=__lg(x);
    return ((1ll<<h2+1)-1)<<(h1-h2+1)|1;
}
signed main(){
    int h1=30,h2=h1/2,x=(1ll<<h1)+(1ll<<h2);
    cout<<"x="<<x<<endl;
    cout<<"4*x="<<4*x<<endl;
    cout<<"f(x)="<<calc(x)<<endl;
    cout<<fixed<<setprecision(10)<<"f(x)/x="<<(double)calc(x)/(double)x<<endl;
}
输出：
CPP
x=1073774592
4*x=4295098368
f(x)=4294901761
f(x)/x=3.9998169011
十分接近 44 了！

结语

其实本人非常非常讨厌这么繁琐的证明过程，但我真的一直很好奇线段树最差的情况是多少，因此就活成了自己最讨厌的样子写了这么一个公式满天飞的证明（笑死）。
我认真思考这个的动机其实就源于上文提到的P6025 线段树。我发现最终得出的公式非常的不错，很可能能让我用比较代数的方法证明这个问题。
其实想要证明开 44 倍空间完全有更简单的推导。但是知道了具体是什么数会逼近四倍空间还是很有意义的！
最终感谢所有的参考资料作者，与阅读到这的你们，谢谢大家！
AI辅助提示
本文使用了 ChatGPT 进行部分数学的推导与验算，所有 AI 的结论均由我验算过。

评论

共 2 条评论，欢迎与作者交流。

正在加载评论...