专栏文章

2025_5_13 T3

EEvan_Leo_Azir
题解参与者 1已保存评论 0

文章操作

快速查看文章及其快照的属性，并进行相关操作。

当前评论
0 条
当前快照
1 份
快照标识符
@mipawcmm
此快照首次捕获于
2025/12/03 09:00
3 个月前
此快照最后确认于
2025/12/03 09:00
3 个月前
查看原文
动态规划神题，难度 CF 2400左右，上位蓝至下位紫
放在 NOIP T3还是有些勉强，省选T1倒是完全充足
首先，我们不考虑题目中 nn 行 mm 列的字符矩阵，先来考虑它的弱化版 : n=1n=1 。即一个字符串
题目中只有一种操作：对折，如下
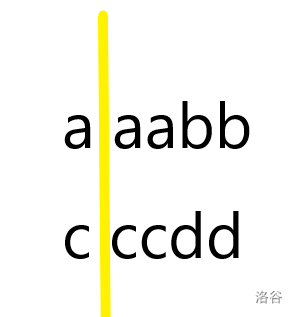
我们沿着图中标出的线对折，即可得到
aabbccddaabb\\ ccdd
具体的，对折就是选择该矩阵的一部分，保证其中的每一行的此部分皆为回文串，随后把回文串的一半删去
当然，也可以对列进行操作
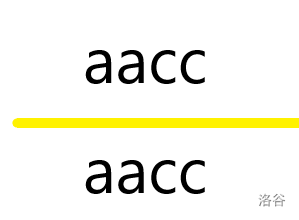
对折后获得
aaccaacc
不难发现，若是在n=1n=1的条件下，对折的操作可以简化为选择字符串的 前\后 缀回文串，并删去它的 左\右 部分，显然，每次操作只会删去前后缀，故考虑动态规划

1.只考虑删前缀

假设 fif_i 表示能否通过一系列手段，删去[1,i−1][1,i-1]的字符，留下[i,n][i,n]的部分
转移显然
fi∣=fj([j,i+i−j−1]为回文串)f_i|=f_j \\([j,i+i-j-1]为回文串)
所以，我们在代码实现中枚举回文中心即可进行转移
初始f1=1f_1=1 (什么都不删)

2.只考虑删后缀

同样，假设 gig_i 表示能否通过一系列手段，删去[i+1,n][i+1,n]的字符，留下[1,i][1,i]的部分
转移显然
gi∣=gj([i+i−j+1,j]为回文串)g_i|=g_j\\([i+i-j+1,j]为回文串)

统计答案

两个动态规划分别表示剩下了前缀，后缀，因为题目需要我们输出合法方案数，故我们实际要统计区间[l,r][l,r]的数量,使区间[l,r][l,r]能通过一系列“对折”产生
显然，我们计后缀和
sufi=∑j=ingjsuf_i=\sum_{j=i}^{n} g_j
答案为
ans=∑i=1nfi×sufians=\sum_{i=1}^{n}f_i\times suf_i
至此,O(n2)O(n^2)的代码完成
我们稍作思考，注意到，题目的字符矩阵的行和列是独立的，故我们将矩阵以每一列哈希后作为一个字符，此时形成同上文的字符串，在其上运行动态规划，之后再将每行哈希后作为字符，运行动态规划后，将行与列的答案相乘即可
代码
CPP
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=1e6+10,Mod=1e9+7;
int n,m,up;
int suf[maxn],has[2][maxn],mul[maxn];
ll res;
bool f[maxn],g[maxn];
vector<vector<char>>a;
int read()
{
	int ret=0,w=1;char ch=0;
	while(ch<'0'||ch>'9') {if(ch=='-') w=-1;ch=getchar();}
	while(ch>='0'&&ch<='9') {ret=(ret<<3)+(ret<<1)+(ch^48);ch=getchar();}
	return ret*w;
}
void pre_all()
{
	mul[0]=1;
	for(int i=1;i<maxn;i++) mul[i]=1ll*mul[i-1]*29%Mod;
}
void inpu()
{
	res=1;
	n=read(),m=read();
	a.resize(n+1);
	for(int i=1;i<=n;i++)
	{
		a[i].resize(m+1);
		for(int j=1;j<=m;j++) cin>>a[i][j];
	}
}
void DP1(int id)
{
	f[1]=1;
	for(int i=2;i<=up;i++) f[i]=0;
	for(int i=2;i<=up;i++) for(int j=1;j<=up;j++)
	{
		if(i-j<1||i+j-1>up||has[id][i+j-1]!=has[id][i-j]) break;
		f[i]|=f[i-j];
		if(f[i]) break;
	}
}
void DP2(int id)
{
	g[up]=1;
	for(int i=1;i<up;i++) g[i]=0;
	for(int i=up-1;i>=1;i--) for(int j=1;j<=up;j++)
	{
		if(i+j>up||i-j+1<1||has[id][i+j]!=has[id][i-j+1]) break;
		g[i]|=g[i+j];
		if(g[i]) break;
	}
}
ll cal()
{
	ll ret=0;
	suf[up+1]=0;
	for(int i=up;i>=1;i--) suf[i]=g[i]+suf[i+1];
	for(int i=1;i<=up;i++) ret+=1ll*f[i]*suf[i];
	return ret;
}
void pre_hash()
{
	for(int j=1;j<=m;j++) for(int i=1;i<=n;i++) has[0][j]=(has[0][j]+1ll*a[i][j]*mul[i-1])%Mod;
	for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) has[1][i]=(has[1][i]+1ll*a[i][j]*mul[j-1])%Mod;
}
void deal(int id)//先列后行 
{
	up=id?n:m;
	DP1(id);
	DP2(id);
	res*=cal();
}
void solve()
{
	inpu();
	pre_hash();
	deal(0);
	deal(1);
	printf("%lld",res);
}
int main()
{
	pre_all();
	int t=1;
	while(t--) solve();
	return 0;
}
时间复杂度O(n2)O(n^2)
(n,mn,m同阶)
注意到，每次转移一个fif_i或者是gig_i,本质上就是在找从ii开始可以扩展出的最大回文区间，最后，只要该区间内有fjf_j或者是gjg_j为真，就将fif_i与gig_i转移为真
因为回文串是连续的，即如果[l,r][l,r]回文,[l+1,r−1][l+1,r-1]也还是回文(l<r−1)(l<r-1)
所以，我们每次保存离当前的 ii 最近的fj=1f_j=1，gj=1g_j=1，记为lstlst，每次判断，从ii到lstlst的这一段字符能否与后面的ii到i+leni+len形成回文（lenlen为ii到lstlst的长度）,如果可以，就把 fif_i,gig_i转为11，并更新lstlst
因为字符串匹配可以用前后缀哈希O(1)O(1)完成，故转移O(1)O(1)，时间复杂度O(n)O(n)，可以通过此题
代码
CPP
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=1e6+10,Mod=1e9+7,Mod2=998244353;
int n,m,up;
int suf[maxn],has[2][maxn],mul[maxn],mul2[maxn],inv2[maxn],sums[maxn],sufs[maxn];
ll res;
bool f[maxn],g[maxn];
vector<vector<char>>a;
int read()
{
	int ret=0,w=1;char ch=0;
	while(ch<'0'||ch>'9') {if(ch=='-') w=-1;ch=getchar();}
	while(ch>='0'&&ch<='9') {ret=(ret<<3)+(ret<<1)+(ch^48);ch=getchar();}
	return ret*w;
}
int qpow(int x,int y,int p)
{
	int ret=1;
	while(y)
	{
		if(y&1) ret=1ll*ret*x%p;
		x=1ll*x*x%p;
		y>>=1;
	}
	return ret;
}
void pre_all()
{//预处理第一，二次hash基底及模数
	mul[0]=1,mul2[0]=1;
	for(int i=1;i<maxn;i++) mul[i]=1ll*mul[i-1]*29%Mod,mul2[i]=1ll*mul2[i-1]*31%Mod2;
	inv2[0]=1,inv2[1]=qpow(mul2[1],Mod2-2,Mod2);
	for(int i=2;i<maxn;i++) inv2[i]=1ll*inv2[i-1]*inv2[1]%Mod2;
}
void inpu()
{
	res=1;
	n=read(),m=read();
	a.resize(n+1);
	for(int i=1;i<=n;i++)
	{
		a[i].resize(m+1);
		for(int j=1;j<=m;j++) cin>>a[i][j];
	}
}
void pre_hash2(int id)
{//对已经哈希过的行，列再哈希一次，求前缀，后缀哈希
	sufs[up+1]=0;
	for(int i=1;i<=up;i++) sums[i]=(sums[i-1]+1ll*has[id][i]*mul2[i-1])%Mod2;
	for(int i=up;i>=1;i--) sufs[i]=(sufs[i+1]+1ll*has[id][i]*mul2[up-i])%Mod2;
}
void DP1(int id)
{
	f[1]=1;
	int lst=1;
	for(int i=2;i<=up;i++) f[i]=0;
	for(int i=2,x,y;i<=up;i++)
	{
		if(i+i-lst-1>up) continue;
		x=(sums[i-1]-sums[lst-1]+Mod2)%Mod2,y=(sufs[i]-sufs[i+i-lst]+Mod2)%Mod2;
		if(1ll*x*inv2[lst-1]%Mod2==1ll*y*inv2[up-i-i+lst+1]%Mod2) lst=i,f[i]=1;
	}
}
void DP2(int id)
{
	g[up]=1;
	int lst=up;
	for(int i=1;i<up;i++) g[i]=0;
	for(int i=up-1,x,y;i>=1;i--)
	{
		if(2*i-lst+1<1) continue;
		x=(sums[lst]-sums[i]+Mod2)%Mod2,y=(sufs[2*i-lst+1]-sufs[i+1]+Mod2)%Mod2;
		if(1ll*x*inv2[i]%Mod2==1ll*y*inv2[up-i]%Mod2) lst=i,g[i]=1;
	}
}
ll cal()
{
	ll ret=0;
	suf[up+1]=0;
	for(int i=up;i>=1;i--) suf[i]=g[i]+suf[i+1];
	for(int i=1;i<=up;i++) ret+=1ll*f[i]*suf[i];
	return ret;
}
void pre_hash()//第一次哈希，将行，列的哈希值求出，压为字符
{
	for(int j=1;j<=m;j++) for(int i=1;i<=n;i++) has[0][j]=(has[0][j]+1ll*a[i][j]*mul[i-1])%Mod;
	for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) has[1][i]=(has[1][i]+1ll*a[i][j]*mul[j-1])%Mod;
}
void deal(int id)
{
	up=id?n:m;
	pre_hash2(id);
	DP1(id);
	DP2(id);
	res*=cal();
}
void solve()
{
	inpu();
	pre_hash();
	deal(0);//对于列，行独立计算
	deal(1);
	printf("%lld",res);
}
int main()
{
	pre_all();
	int t=1;
	while(t--) solve();
	return 0;
}

评论

共 0 条评论，欢迎与作者交流。

正在加载评论...