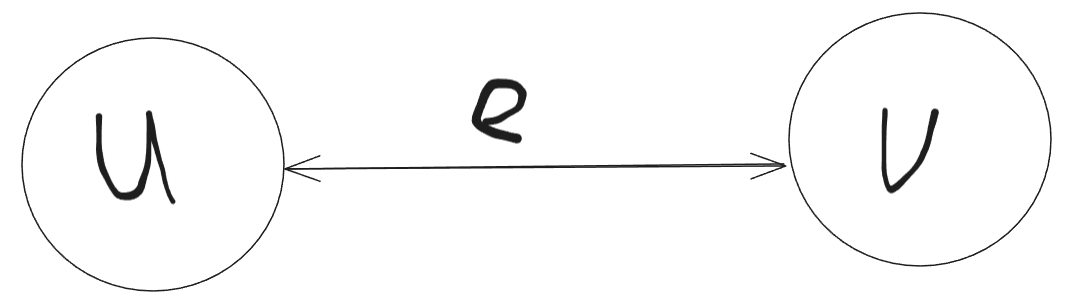0.小引

图论是个~~非常好玩~~的东西，无论是简单的 B3862 还是困难的 P10787，~~甚至是 A+B Problem~~ 都可以用图论解决。

1.图的概念

这里不想用那种肥肠专业的术语，不易理解。

只介绍一些关键的概念。

设一个图

G

具有

n

个节点和

m

条边，其中点编号为

1,2,\dots ,n

，边编号为

1,2,\dots m

。

以下节点简称为点。

1.1 点集与边集

1.1.1 点集

设一个集合

V={1,2\dots ,n}

，即这个集合里面包含

G

的所有点，那么就称

V

是图

G

的点集。

1.1.2 边集

设一个集合

E={1,2\dots ,m}

，即这个集合里面包含

G

的所有边，那么就称

E

是图

G

的边集，此时边数 $m=|E|$ 。

那么我们就可以把图

G

表示为

G=(V(G),E(G))

。

1.2 图的类型

1.2.1 有向图

故名思意，有方向的图。

当图

G

为有向图时，取其中的两个点

u,v

，满足

u,v\in V

。

那么如果有一条边

e\in E

连接了

u,v

，那么表示为

e=u\to v

，也就是

u

可以到

v

，但是

v

到不了

u

，结合图片更好理解。

此时

e

是一条有向边。

1.2.2 无向图

故名思意，没有方向的图。

当图

G

为无向图时，取其中的两个点

u,v

，满足

u,v\in V

。

那么如果有一条边

e\in E

连接了

u,v

，那么表示为

e=(u,v)

，也就是

u

可以到

v

，而且

v

也可以到

u

，结合图片更好理解。

此时

e

是一条无向边。

1.2.3 混合图

既有有向边又有无向边的图。

1.3 度

1.3.1 度的基本

与一个顶点

v

相关联的边的数量称为这个点的度，记作

d(v)

，对于一条无向边

(u,v)

，每一条边都对

d(v)

有

2

的贡献。

无向图的基本定理：每条边都会产生 $2$ 的贡献，记作 $\sum_{u\in V}d(u)=2 |E|$ 。

如果此时一个点

v

的度

d(v)=1

，则称这个点是叶子节点。

1.3.2 入度与出度

对于一个点

v

，称以

v

为终点的边数为点

v

的入度，记作

d^-(v)

；称以

v

为起点的边数为点

v

的出度，记作

d^+(v)

。

定理1：入度与出度之和等于度，记作 $d(v)=d^+(v)+d^-(v)$ 。

定理2：入度等于出度等于边数，记作 $\sum_{u\in V}d^+(v)=\sum_{u\in V}d^-(v)=|E|$ 。

1.4 路径

途径：连接了若干个相邻的点的序列，记作 $u_0\to u_1 \dots \to u_k$ 。
迹：不经过重复边的途径。
回路：起点等于终点的迹。
环：对于一条回路，除了 $u_0=u_k$ ，没有其他的 $u_i=u_j(i=j,i\neq 0,k,j\neq 0,k)$ 。

2.图的存储

以下的时间复杂度无特殊说明都为遍历图的复杂度。

2.1 邻接矩阵

使用二维数组 g 存边。

对于一条无权边 $g_{i,j}=1$ 表示存在一条边 $e=(u,v)$ 。
对于一条有权边 $g_{i,j}=w$ 表示存在一条边 $e=(u,v)$ 的边权为 $w$ 。

空间复杂度：

O(n^2)

，时间复杂度：

O(n^2)

。

代码

CPP

while(m--){
    int u,v,w;
    cin>>u>>v>>w;
    g[u][v]=w;
}

2.2 邻接表

使用 vector<int>g[N] 存边。

对于无权图，g 中一般存放终点。
对于有权图，vector<int>g[N] 可以变为 vector<edge>g[N]，结构体中一般存放终点和边权。

空间复杂度：

O(m)

，时间复杂度：

O(n+m)

。

代码

CPP

while(m--){
    int u,v,w;
    cin>>u>>v>>w;
    g[u].push_back({v,w});
}

2.3 前向星

用链表数据存储的邻接表，常数较小。

代码

CPP

int head[N],nxt[M<<1],to[M<<1],g[M<<1],cnt=1; 
void add(int u,int v,int w){
	nxt[++cnt]=head[u];
	head[u]=cnt;
	to[cnt]=v;
	g[cnt]=w;
}

2.4 例题

B3613 图的存储与出边的排序

B3643 图的存储

3.图的遍历

3.1 遍历出边

邻接表代码

CPP

for(int i=0;i<g[u].size();i++)
	int v=g[i].v,w=g[i].w;
	//...
}

前向星代码

CPP

for(int i=head[u];i;i=nxt[i]){
	int v=to[i],w=g[i];
	//...
}

3.2 深搜 DFS

一条路走到底，不撞南墙不回头。

通过递归实现，一般代码结构如下：

CPP

void dfs(int u){
	vis[u]=1;//经过v，打上标记
	for(...){ //遍历出边
		int v=...;
		if(!vis[v]){//如果当前节点没经过 
			dfs(v);
		}
	}
}

如果想了解其底层原理，参考 OI Wiki——DFS（搜索）。

3.3 广搜 BFS

一层一层的遍历图。在 BFS 结束时，每个节点都是通过从起点到该点的最短路径访问的。

所以许多最短路算法都是通过 BFS 实现的，见第 4 章。

通过队列实现，一般代码结构如下：

CPP

void bfs(int s){
	queue<int>q;
	vis[s]=1;
	q.push(s);
	while(!q.empty()){
		int u=q.front();q.pop();
		for(...){//遍历
			if(!vis[v]){
				q.push(v);
				vis[v]=1;
			}
		}
	} 
}

4.最短路问题

点与点之间的长度最短的路径。

4.1 Floyd 算法

一种求多源/全源最短路的算法。

设

f_{k,i,j}

表示从

i

到

j

只允许经过

1,2,\dots,k

的最短路径。

所以当我们想求

i

到

j

的最短路时，答案就是

f_{n,x,y}

。

容易发现，其实

k

的第一维对答案没有影响。

证明

每个 f[k][i][j] 都是由 f[k-1][i][j] 转移而来的，容易发现 f[k][i][j] 一定不大于 f[k-1][i][j]，所以其实 f[k][i][j] 可以直接覆盖，即可以省略第一维，类似 DP 的状态压缩。

所以容易发现，当前的

f_{i,j}

可以看作

i

到

k

的最短路径与

k

到

j

的最短路径之和再和

f_{i,j}

取最小值，即 f[i][j]=min(f[i][j],f[i][k]+f[j][k])。

代码

CPP

void floyd(){
	for(int k=1;k<=n;k++){
		for(int i=1;i<=n;i++){
			for(int j=1;j<=n;j++){
				f[i][j]=min(f[i][j],f[i][k]+f[j][k]);
			}
		}
	}
}

例题

把最短路径化作能否到达，即 if(f[i][k]&&f[k][j]) f[i][j]=1;。

以上都是 Floyd 的板子。

以上是变种题，有一定思维难度。

图论：从入门到提高

文章操作