题解：AT_xmascon20_f Famous in Russia

前言

题解字数较多，但作者认为还是相对浅显易懂的。

第一部分：这个题到底在干啥？

正如副标题所言，我们拿到这题，似乎无从下手。在此之前，我们不妨考虑这样一个更加简单的问题：

问题 1：

给定 $a_1\sim a_n,b_1\sim b_n$ ，令 $k=n$ ，求做菜吃菜最短时间。

解析：将菜品按照

b_i

从大到小排序依次制作，答案为

\max_{i=1}^n(b_i+\sum_{j=1}^ia_j)

。

证明：

利用调整法。对于一个不是按照 $b_i$ 从大到小排序的菜品序列，一定能找到下标 $i$ （ $1\le i<n$ ），使得 $b_i<b_{i+1}$ 。

设 $\sum_{j=1}^{i-1}a_j=x$ ，那么 $i$ 处的答案为 $ans_i=x+a_i+b_i$ ， $i+1$ 处的答案为 $ans_{i+1}=x+a_i+a_{i+1}+b_{i+1}$ 。

交换 $i,i+1$ 菜品，此时对于 $i+2\sim n$ 以及 $1\sim i-1$ 处，答案不变，而 $i,i+1$ 处的答案分别为 $ans'_i=x+a_{i+1}+b_{i+1},ans'_{i+1}=x+a_i+a_{i+1}+b_i$ 。

由于 $b_i<b_{i+1}$ ，因此 $ans'_{i+1}<ans_{i+1}$ 。

由于 $b_i<b_{i+1}$ ，因此 $b_i<a_{i+1}+b_{i+1}$ ，因此 $x+a_i+b_i<x+a_i+a_{i+1}+b_{i+1}$ ，因此 $ans_i<ans_{i+1}$ 。

显然 $x+a_{i+1}+b_{i+1}<x+a_i+a_{i+1}+b_{i+1}$ ，因此 $ans'_i<ans_{i+1}$ 。

因此， $\max(ans_i,ans_{i+1})>\max(ans'_i,ans'_{i+1})$ ，交换显然更优。

对于上述问题，有没有一个更简单的刻画答案的方式？答案是肯定的。只需要将菜品按照

b_i

从小到大排序，维护答案

ans

。遍历

i=1\sim n

，令

ans:=\max(ans,b_i)+a_i

。这本质只是倒过来计算答案。

问题 2：

给定 $a_1\sim a_n,b_1\sim b_n$ ，对于每个 $k$ ，求做菜吃菜最短时间。

解析：首先，将菜品按照

b_i

从小到大排序。忽略

a_i

被钦定为

0

的菜品，在最后将答案与

b_n

取较大值即可。接下来，研究以下 dp：

dp_{i,j}=\min(dp_{i-1,j},\max(dp_{i-1,j-1},b_i)+a_i)

可以发现，

dp_{i,j}

表示在前

i

个菜品中挑选

j

个，仅它们的

a_j

不被钦定为

0

，此时的答案最小值。那么对于每个

k

，答案即为

ans_k=\max(dp_{n,k},b_n)

。

第二部分：有点头绪了，我们来优化这个 dp 吧！

一个全新的问题出现在我们面前：咋优化这个 dp？我们需要利用一些结论。

结论 1：

$dp_{i,j}\le dp_{i,j+1},dp_{i,j}\ge dp_{i+1,j}$ 。

证明：

利用定义，可以发现在前 $i+1$ 个菜品中挑选 $j$ 个肯定不比在前 $i$ 个菜品中挑选劣，因为多了第 $i+1$ 个菜品供以选择。在前 $i$ 个菜品中挑选 $j$ 个肯定不比挑选 $j+1$ 个劣，因为多了一个需要选择的菜品。

根据结论 1 我们可以得知，对于每个

i

，我们可以找到唯一一个

j_i

（

1\le j_i\le i+1

）使得对于所有

j<j_i

，

dp_{i,j}\le b_i

。

结论 2：

$j_i\le j_{i+1}$ 。

证明：

根据结论 1，对于 $j<j_i$ ， $dp_{i+1,j}\le dp_{i,j}\le b_i\le b_{i+1}$ ，因此 $j_{i+1}\ge j_i$ 。

结论 3（重要）：

对于 $j<j_i$ ， $dp_{i,j}=dp_{i-1,j}$ 。

证明：

由于 $dp_{i,j}=\min(dp_{i-1,j},\max(dp_{i-1,j-1},b_i)+a_i)$ ，而 $\max(dp_{i-1,j-1},b_i)+a_i>b_i$ ， $dp_{i,j}\le b_i$ ，所以 $dp_{i,j}=dp_{i-1,j}$ 。

结论 4（重要）：

对于 $j>j_i$ ， $dp_{i,j}=\min(dp_{i-1,j},dp_{i-1,j-1}+a_i)$ 。

证明：

由于 $dp_{i,j}=\min(dp_{i-1,j},\max(dp_{i-1,j-1},b_i)+a_i)$ ，而 $dp_{i-1,j-1}\ge dp_{i,j-1}>b_i$ ，所以 $dp_{i,j}=\min(dp_{i-1,j},dp_{i-1,j-1}+a_i)$ 。

铺天盖地的这么多结论，我们该如何利用它们呢？我们从差分数组考虑。

记

dif_{i,j}=dp_{i,j}-dp_{i,j-1}

（

j_i\le j\le i

）。

对于 $j=j_i$ ，由于 $dp_{i,j-1}=dp_{i-1,j-1}\le b_i$ ，所以 $dp_{i,j}=\min(dp_{i-1,j},b_i+a_i)$ 。如果 $dp_{i-1,j}\le b_i+a_i$ ，那么 $dif_{i,j}=dif_{i-1,j}$ ，否则 $dif_{i,j}=a_i+b_i-dp_{i,j-1}$ 。
对于 $j>j_i$ ，利用结论 4，祭出下面这张图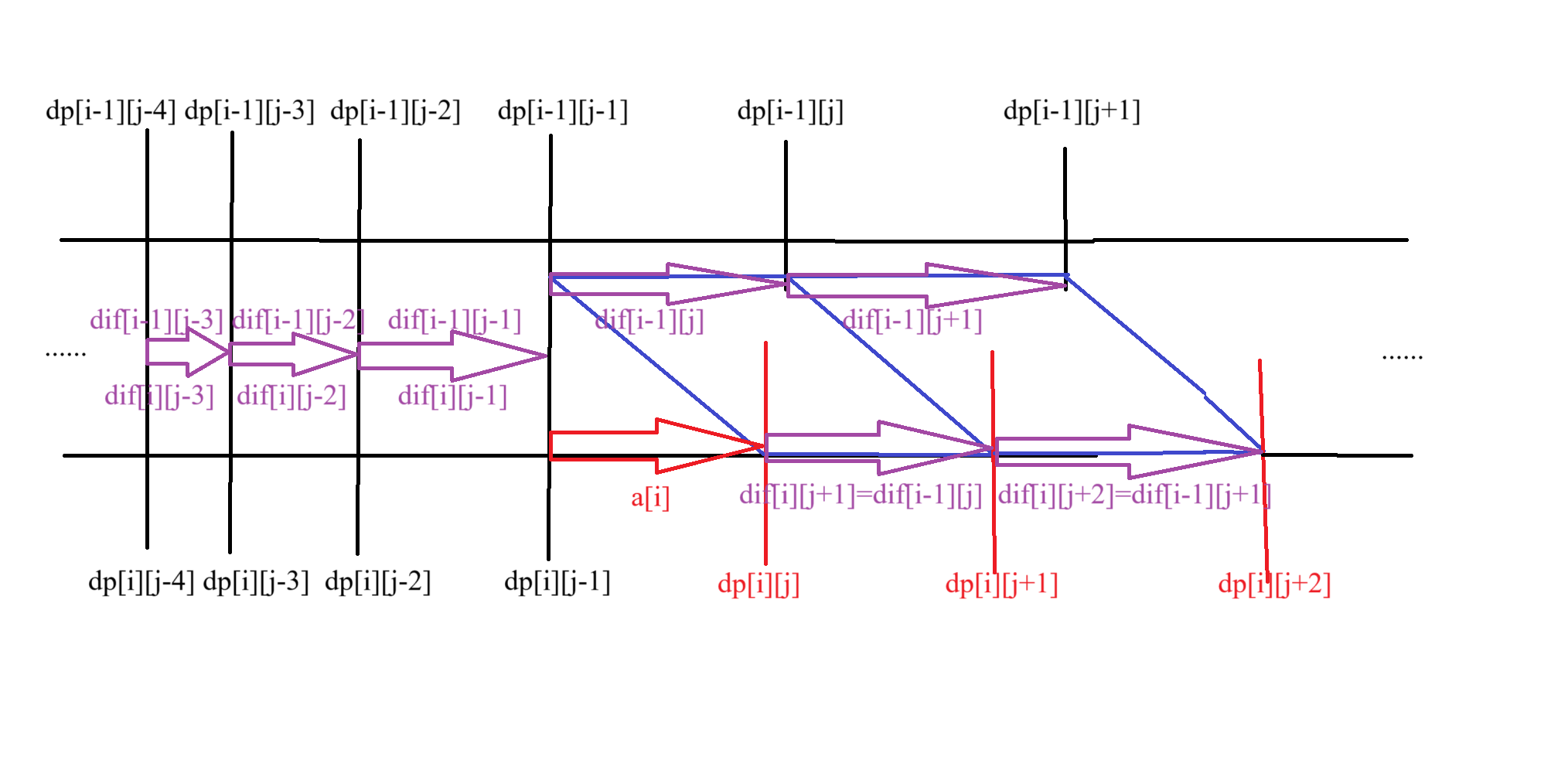：根据图可以发现，差分数组 $dif_{i,j_i+1}\sim dif_{i,i}$ 本质上只是在差分数组 $dif_{i-1,j_i+1}\sim dif_{i-1,i-1}$ 中插入了一个 $a_i$ ，插入的位置 $j$ 满足 $dif_{i-1,j}>a_i\ge dif_{i-1,j-1}$ 。

如上可得，对于

j>j_i+1

，

dif_{i,j}\ge dif_{i,j-1}

。而对于

j=j_i

时

dif

的复杂讨论，可以总结为以下两点：

$dif_{i,j_i}$ 对我们而言作用属实不大！我们更看重的是 $dp_{i,j_i}-b_i$ 而非 $dp_{i,j_i}-dp_{i,j_i-1}$ ！
在这里，我们如果将 $dif_{i,j_i}$ 的定义修改为 $dp_{i,j_i}-b_i$ ，我们就有能力扩展 $j>j_i$ 时的发现，甚至于将它与 $j=j_i$ 时的发现合并！

所以，我们修改差分数组

dif

的定义。此时，记 $dif_{i,j}=dp_{i,j}-dp_{i,j-1}$ （ $j_i<j\le i$ ），记 $dif_{i,j_i}=dp_{i,j_i}-b_i$ 。

那么，

dif_{i,j}\ge dif_{i,j-1}

。差分数组

dif_{i,j_i}\sim dif_{i,i}

本质上只是：

根据结论 3，在差分数组 $dif_{i-1,j_{i-1}}\sim dif_{i-1,i-1}$ 中切掉 $dif_{i-1,j_{i-1}}\sim dif_{i-1,j_i-1}$ 不用。（步骤 1）
将 $dif_{i-1,j_i}$ 通过某种方式修改为 $dp_{i,j_i}-b_i$ 。（步骤 2）
在 $dif_{i-1,j_i}\sim dif_{i-1,i-1}$ 中插入一个 $a_i$ ，插入的位置 $j$ 满足 $dif_{i-1,j}>a_i\ge dif_{i-1,j-1}$ 。（步骤 3）
得到 $dif_{i,j_i}\sim dif_{i,i}$ 。

这样，我们就有能力利用小根堆维护差分数组

dif

：

每遇到一个 $i$ （ $2\le i\le n$ ），我们记 $cur=b_{i-1},id=j_{i-1}$ ，然后依次弹出堆顶存储的元素 $top$ ：
- 令 $cur:=cur+top$ 。
- 此时 $cur=dp_{i,id}$ 。根据结论 2， $id<j_i,cur=dp_{i,id}=dp_{n,id}$ ，我们显然可以在这里将 $\max(b_n,cur)$ 贡献到 $ans_{id}$ 当中。
- 令 $id:=id+1$ 。
直到 $cur+top>b_i$ 为止（此时堆顶存储的是 $top$ ）。完成步骤 1。
此时， $j_i=id$ 。我们想让这个堆中存储的东西变成 $dif_{i,id}\sim dif_{i,i}$ ，具体地：
- 堆中的 $top$ 是 $dif_{i-1,id}$ 。此时去除 $top$ ，插入 $cur+top-b_i$ （ $cur+top$ 是 $dp_{i,id}$ 的值）。完成步骤 2。
- 插入一个 $a_i$ 。完成步骤 3。

初始时堆中只有一个

a_1

。

第三部分：道理我都懂了，但是我们不知道 $a_i$ ，该咋办？

我们总结一下。

通过前两部分，我们得到了一个基于小根堆的一个算法，快速求解 dp 值贡献到答案中。但由于我们不知道

a_i

的值，这个算法似乎没什么实际用途。除非，我们把这个小根堆本身压入一个新的 dp，形成 dp 套 dp。

略微修改一下上述算法，将

id

变为全局变量便于操作，得到以下算法：

初始时堆中只有一个 $a_1$ 。记 $id=1$ 。
每遇到一个 $i$ （ $2\le i\le n$ ），记 $cur=b_{i-1}$ ，依次弹出堆顶存储的元素 $top$ ：
- 令 $cur:=cur+top$ 。
- 将 $\max(b_n,cur)$ 贡献到 $ans_{id}$ 当中。
- 令 $id:=id+1$ 。
直到 $cur+top>b_i$ 为止。
去除 $top$ ，插入 $cur+top-b_i$ 。
插入一个 $a_i$ （根据先前插入 $a_i$ 的规定，插入相同数值的元素将会被认为按照插入顺序从前到后排列）。前往 $i+1$ 循环上述操作。

那我们的任务就是，将这个小根堆压入新的 dp 状态中。对于一个小根堆中的一个元素

x

，我们需要知道：

$x$ 的值。
$i$ 的值，为了得知 $b_{i-1}$ 的值。
处在 $x$ 前面的所有元素（包括 $x$ 本身）的数量 $j$ ，为了得知答案贡献到 $ans$ 的哪个下标（ $id=j$ ）。
处在 $x$ 前面的所有元素（包括 $x$ 本身）的和 $sum$ ，为了结合 $i$ 的值得知 $cur$ 的值。

记

g_{i,j,sum,x}

表示小根堆满足下标所示条件的

a_1\sim a_{i-1}

的组数。对于

a_i\in[1,v]

，我们尝试追踪

x

的去向：

首先，如果 $sum+b_{i-1}\le b_i$ ，这意味着 $x$ 这个元素将会在这一轮被弹出，将 $\max(b_n,sum+b_{i-1})\times g_{i,j,sum,x}\times v^{n-i+1}$ 贡献到 $ans_j$ 中，不做任何转移。其中 $v^{n-i+1}$ 代表着 $a_i\sim a_n$ 的值任意。
如果 $sum+b_{i-1}>b_i$ $s u m + b_{i - 1} > b_{i}$ ，这意味着 $x$ $x$ 将会在这一轮被保留。记 $w=\min(x,sum+b_{i-1}-b_i)$ $w = min (x, s u m + b_{i - 1} - b_{i})$ 。 $w$ $w$ 将会是 $x$ $x$ 在这一轮之后的值。枚举 $a_i$ $a_{i}$ 。
- 如果 $a_i<w$ ，那么 $g_{i+1,j+1,sum+b_{i-1}-b_i+a_i,w}\larr g_{i,j,sum,x}$ 。
- 如果 $a_i\ge w$ ，那么 $g_{i+1,j,sum+b_{i-1}-b_i,w}\larr g_{i,j,sum,x}$ 。
- 在这里，根据插入 $a_i$ 的规定，我们需要时刻记住，小根堆中的值是按大小为第一关键字，插入顺序为第二关键字排序的。因此 $a_i=w$ 时将会归类到 $a_i>w$ 的情况中。

据此，我们解决了几乎整道题目。上述 dp 几乎完美，只有一个问题：列出的转移式只是针对

a_1\sim a_{i-1}

这种以前已经被插入进来的元素进行实时追踪，插入的

a_i

该如何统计到

g

中并随着转移在以后追踪呢？

第四部分：解决新加入的 $a_i$ 无法统计的问题

绞尽脑汁，我们似乎没有办法解决这个问题。我们的状态定义还是太简单了，似乎无法支持我们定位插入的

a_i

的位置。不妨更改状态，我们额外记一个信息：

处在 $x$ 后面的最靠前的元素（不包括 $x$ ）的值 $nxt$ 。

根据插入

a_i

的规定，我们需要时刻记住，小根堆中的值是按大小为第一关键字，插入顺序为第二关键字排序的。这样，我们得知假如

a_i

被插入到

x

和

nxt

之间，那么它一定满足

x\le a_i<nxt

。

对于每个

x

，在

x

处定位所有满足

x\le a_i<nxt

的

a_i

。具体地，记

f_{i,j,sum,x,nxt}

表示小根堆满足下标所示条件的

a_1\sim a_{i-1}

的组数。接下来定位

x

的去向以及追踪

a_i

：

如果 $sum+b_{i-1}\le b_i$ ，则将 $\max(b_n,sum+b_{i-1})\times f_{i,j,sum,x,nxt}\times v^{n-i+1}$ 贡献到 $ans_j$ 中，不做任何转移。
如果 $sum+b_{i-1}>b_i$ $s u m + b_{i - 1} > b_{i}$ ，记 $w=\min(x,sum+b_{i-1}-b_i)$ $w = min (x, s u m + b_{i - 1} - b_{i})$ 。枚举 $a_i$ $a_{i}$ 。
- 如果 $a_i<w$ ，那么 $f_{i+1,j+1,sum+b_{i-1}-b_i+a_i,w,nxt}\larr f_{i,j,sum,x,nxt}$ 。
- 如果 $a_i\ge w$ ，那么 $f_{i+1,j,sum+b_{i-1}-b_i,w,\min(a_i,nxt)}\larr f_{i,j,sum,x,nxt}$ 。
追踪满足 $x\le a_i<nxt$ 的 $a_i$ ，也就是令 $f_{i+1,j+1,sum+b_{i-1}-b_i+a_i,a_i,nxt}\larr f_{i,j,sum,x,nxt}$ 。这使得我们的视角转换到 $a_i$ 上。

到此为止，问题基本完成，剩下的便是一些小角箱子（corner case），例如小根堆中不存在元素该怎么办，

nxt

不存在该怎么办，以及

a_i

若插入到小根堆堆头则上述转移无法统计到它等问题。这一部分留给读者自行推导，以加深理解。

总结

这个做法的时间复杂度为

O(n^3v^4)

，空间复杂度经滚动数组可以优化到

O(n^2v^3)

。

题解：AT_xmascon20_f Famous in Russia

文章操作

前言

第一部分：这个题到底在干啥？

第二部分：有点头绪了，我们来优化这个 dp 吧！

第三部分：道理我都懂了，但是我们不知道 $a_i$ ，该咋办？

第四部分：解决新加入的 $a_i$ 无法统计的问题

总结

相关推荐

评论

题解：AT_xmascon20_f Famous in Russia

文章操作

前言

第一部分：这个题到底在干啥？

第二部分：有点头绪了，我们来优化这个 dp 吧！

第三部分：道理我都懂了，但是我们不知道 aia_iai​，该咋办？

第四部分：解决新加入的 aia_iai​ 无法统计的问题

总结

相关推荐

评论

第三部分：道理我都懂了，但是我们不知道 $a_i$ ，该咋办？

第四部分：解决新加入的 $a_i$ 无法统计的问题