CF2096D Wonderful Lightbulbs 题解

\rm Problem:

Wonderful Lightbulbs

被这个 D 吊打了，想了

40

分钟。

题意

平面上每个整点初始有权值

0

，有一个位置有权值

1

。

每次操作为：选择一个

(x,y)

，将

(x,y),(x,y+1),(x+1,y−1),(x+1,y)

上的权值异或

1

。

现在给出若干次操作后权值为

1

的共

n

个点，求初始权值为

1

的点。

1\le n\le 2\times10^5

做法

不妨这样看待操作的四个点：

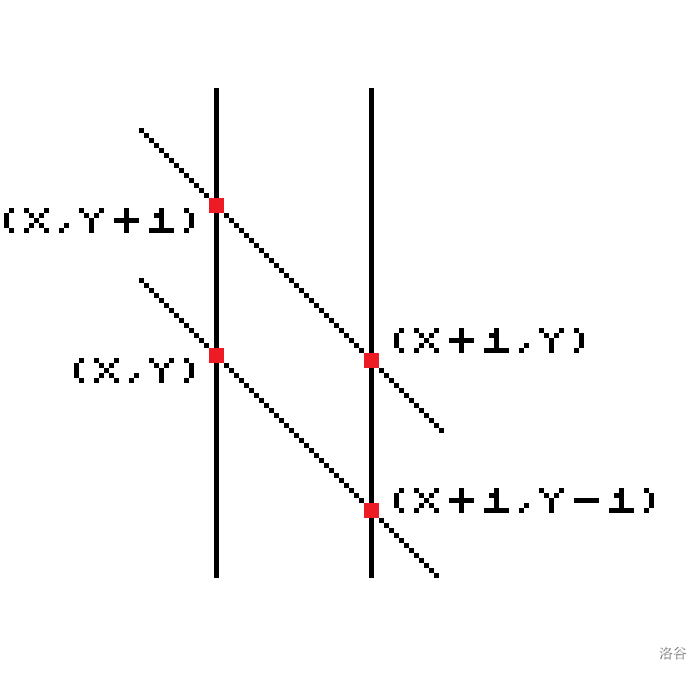
发现每条竖线，每条斜线的异或和都不会改变。

于是我们找到异或和为

1

的竖线和斜线即可确定初始的点。

代码

CPP

#include<bits/stdc++.h>
#define cint const int
#define uint unsigned int
#define cuint const unsigned int
#define ll long long
#define cll const long long
#define ull unsigned long long
#define cull const unsigned long long
#define sh short
#define csh const short
#define ush unsigned short
#define cush const unsigned short
using namespace std;
int read()
{
	int num=0,zf=1;
	char ch=getchar();
	while(ch<'0'||ch>'9')
	{
		if(ch=='-')zf=-1;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9')
	{
		num=(num<<1)+(num<<3)+(ch-'0');
		ch=getchar();
	}
	return num*zf;
}
void print(cint x)
{
	if(x<10)
	{
		putchar(x+'0');
		return;
	}
	print(x/10);
	putchar(x%10+'0');
}
void princh(cint x,const char ch)
{
	if(x<0)
	{
		putchar('-');
		print(-x);
		putchar(ch);
		return;
	}
	print(x);
	putchar(ch);
}
int n;
map<int,bool>X,Y;
int x[200001],y[200001];
int ansx,ansy;
void solve()
{
	n=read();
	X.clear();
	Y.clear();
	for(int i=1;i<=n;++i)
	{
		x[i]=read();
		y[i]=read();
		X[x[i]]^=1;
		Y[x[i]+y[i]]^=1;
	}
	for(int i=1;i<=n;++i)
	{
		if(X[x[i]])ansx=x[i];
		if(Y[x[i]+y[i]])ansy=x[i]+y[i];
	}
	princh(ansx,' ');
	princh(ansy-ansx,'\n');
}
int main()
{
	//freopen(".in","r",stdin);
	//freopen(".out","w",stdout);
	int T=read();
	while(T--)solve();
	return 0;
}

CF2096D Wonderful Lightbulbs 题解

文章操作

题意

做法

代码

相关推荐

评论

CF2096D Wonderful Lightbulbs 题解