第三场积分赛 yky出题部分 解题报告

负责了比较有强度的三道题，非常对不起大家！！！or2

原题：P6111 [USACO18JAN] MooTube S

关键词：dfs。

注意到数据范围非常友好，可以支持 $O(nq)$ 复杂度的做法，那么我们自然可以考虑每次询问单独处理，去做一轮复杂度为 $O(n)$ 的操作找出答案即可。

所以对于每次询问，我们都做一次以 $v_i$ 为起点的 dfs，期间记录到达某个节点时，经过的边权的最小值，最后暴力统计出这个最小值大于等于 $k_i$ 的节点数即可。这样单次询问复杂度是 $O(n)$ 的。

本题另有数据范围增强的版本：P4185 [USACO18JAN] MooTube G，感兴趣的话也可以去看一眼。

原题：P4568 [JLOI2011] 飞行路线

关键词：分层图最短路。

这里介绍一种处理最短路问题时，常会用到的建图方法：分层图。

分层图，顾名思义，会在图原本的基础上额外多建几层，以便满足题目中的一些特殊限制或者要求。

我们以本题为例，在最基础的最短路问题上，这一题多加了一个特性：可以选择一条边，使它的边权暂时变为 0 并通过。那么我们不妨将建出一个 $k+1$ 层的图，层数为第 $0$ 层到第 $k$ 层，位于第 $i$ 层，则表示已经使用了 $i$ 次上述的特性。

比如根据样例中的数据，我们就可以建出如下的图：

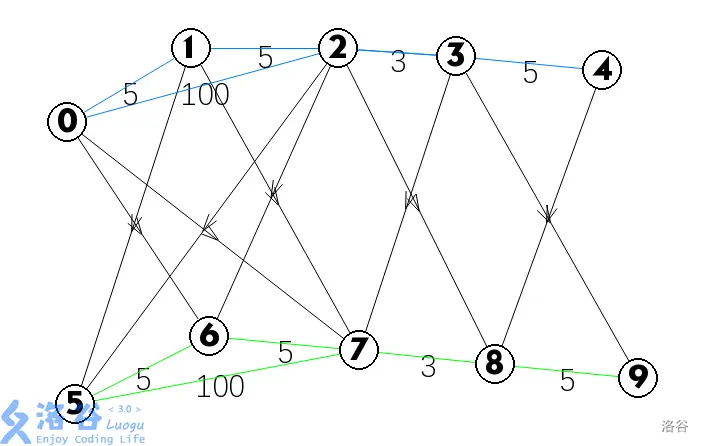
其中在每条边上，都向下一层伸出一对单向的，边权为 $0$ 的边，走过这条边到下一层就表示表示使用了一次特性。

那么建好图后，事情就非常简单了：依旧以第 $0$ 层中起点对应的点开始，跑一次最短路，随后统计每层中终点对应的点的距离，取最小值即可。

分层图的思想是非常巧妙的，感兴趣的话，下面是两道练习题：

改编自：CF559C Gerald and Giant Chess 和 P1002 [NOIP 2002 普及组] 过河卒

关键词：DP，容斥，组合计数。

老题新做，注意到虽然棋盘盘面变得非常大，但马的控制点（或者我们统称做障碍）却依然很少，不妨从每个障碍上下手。

如何统计不经过任何障碍，到达终点的路径数呢？直接统计是非常不现实的，所以我们可以考虑首先算出不考虑障碍的情况下，到达终点的所有路径数（通过组合数可以很快计算），然后再减去经过了障碍点的情况。

为了统计这些障碍点的情况，我们不妨先把所有的障碍点，按照先根据 $x$ 再根据 $y$ 的顺序排序。设 $f_i$ 为不经过任何其他障碍点，走到排序后第 $i$ 个障碍点的路径数。

对于每个障碍点 $i$，我们先算出不考虑其他障碍点的情况下，到达当前点的所有路径数，随后再枚举第 $1$ 到 $i-1$ 个关键点，减去先经过了这些点的情况。

具体来讲，假设我们枚举到了 $j$，假设 $y_i<y_j$，那么不可能先经过 $j$ 再经过 $i$，所以直接跳过即可。

反之，则将 $f_j$ 乘上由点 $j$ 到点 $i$ 的所有路径数，得到了由起点到达 $i$，且经过的第一个障碍点是 $j$ 的路径数。给 $f_i$ 减去这个路径数即可。

枚举完前 $i-1$ 个点后，即可得到不经过前面任何障碍点到达 $i$ 的路径数。

为了方便处理，我们不妨把 $(n,m)$ 也视为一个“障碍点”参与计算，最后得出答案即可。

为了更快地计算组合数，需要预处理出到 $2 \times 10^5$ 的阶乘和阶乘的逆元。这样就可实现 $O(1)$ 计算组合数。

预处理复杂度为 $O(nlogn)$，求解复杂度为 $O(Tk^2)$，其中 $k$ 为障碍点数量，最大不超过 10。

本题的主要做法同时也是 2025 ICPC 武汉邀请赛 G Path Summing Problem 的一部分。感兴趣的话可以去看看这道硬控了我们三小时的题。