专栏文章

qoj#11723 I've Got Friends

ccomplexor管理员
个人记录参与者 1已保存评论 0

文章操作

快速查看文章及其快照的属性，并进行相关操作。

当前评论
0 条
当前快照
1 份
快照标识符
@minjufjg
此快照首次捕获于
2025/12/02 03:35
3 个月前
此快照最后确认于
2025/12/02 03:35
3 个月前
查看原文

题目大意

有 nn 个人，每个人 ii 有两种喜爱食物 fi,0,fi,1(fi,0≠fi,1)f_{i,0},f_{i,1}(f_{i,0}\neq f_{i,1})。定义这 nn 个人的友谊集合为 S={(i,j)∣i<j∧{fi,0,fi,1}∩{fj,0,fj,1}≠∅}S=\{(i,j)|i<j\wedge \{f_{i,0},f_{i,1}\}\cap\{f_{j,0},f_{j,1}\}\neq\varnothing\} 。
现在给定 nn 和 SS，要求构造一组 f1,0,f1,1,f2,0,f2,1,…,fn,0,fn,1f_{1,0},f_{1,1},f_{2,0},f_{2,1},\dots,f_{n,0},f_{n,1}，使得这 nn 个人的友谊集合为给出的 SS，或报告无解。
设 m=∣S∣m = |S|，则 1≤n≤105,0≤m≤1051\leq n\leq 10^5,0\leq m\leq 10^5，SS 中每个二元组均由 [1,n][1,n] 内的两个不同正整数构成，且没有两个相同的二元组。

解题过程

将每个人看作连接 (fi,0,fi,1)(f_{i,0},f_{i,1}) 的边，那么 SS 就是所有有公共端点的边对。则原题转化为求出一个 nn 条边的多重图（即允许重边的图）GG，使得其线图 (line graph) 为给定的图 HH，SS 即为 HH 的边集。
下面探讨 GG 不存在重边并且连通的情况（连通块之间显然没有影响），最后会说明存在重边的情况只需简单处理。内容参考了 Van Rooij 和 Wilf 发表于 1965 年的论文以及 Roussopoulos 发表于 1973 年的论文（见参考资料）。
定理 1：图 HH 是线图，当且仅当存在一系列子图 C1,C2,…,CkC_1,C_2,\dots,C_k，其中每个 CiC_i 都是完全图，且 HH 中每条边恰好在一个子图中，每个点在不超过两个子图中。称这一系列子图为一组“划分”，其中每个子图为一个“单元”。
这个定理很容易证明，线图划分中每个单元就对应了原图中与一个顶点相连的所有边，如果得到了划分那么构造出原图是容易的。这个定理在下面的证明和算法中非常重要，现在算法的目的就变成找到一组划分。
为了便于表述，下面记 a∼ba\sim b 表示点 aa 和点 bb 之间存在边，a≁ba\nsim b 表示 aa 和 bb 之间不存在边。
在关于线图的研究中，有一种重要的结构是”三角形“（三元环），即三个点 (a,b,c)(a,b,c) 满足 a∼b,b∼c,c∼aa\sim b,b\sim c, c\sim a。同样重要的还有三角形的奇偶性：定义一个三角形 (a,b,c)(a,b,c) 是奇的，当且仅当图中存在一个点 dd，恰好与 a,b,ca,b,c 中 11 个或 33 个点相邻；否则这个三角形是偶的。
下面的引理就可以体现三角形和其奇偶性的作用：
引理 1：在线图 HH 的划分中，设边 (a,b)(a,b) 所在单元为 CC，那么所有满足 (a,b,c)(a,b,c) 为奇三角形的 cc 都满足 c∈Cc\in C。
证明考虑反证：假设存在 c∉Cc\notin C 使得 (a,b,c)(a,b,c) 为奇三角形，那么存在另一点 dd 恰好与 a,b,ca,b,c 中的一个或者三个点相邻。
  1. 若 dd 只与 aa 相邻（bb 同理），那么显然 d∉Cd\notin C。又因为 d≁cd\nsim c，所以 (a,d),(a,c)(a,d),(a,c) 属于两个不同单元且都不是 CC，那么 aa 出现在三个单元中，矛盾；
  2. 若 dd 只与 cc 相邻，那么 (c,a),(c,b),(c,d)(c,a),(c,b),(c,d) 必须属于三个不同单元，矛盾；
  3. 若 dd 与 a,b,ca,b,c 都相邻且 d∈Cd\in C，那么同上 (c,a),(c,b),(c,d)(c,a),(c,b),(c,d) 属于三个不同单元，矛盾；
  4. 若 dd 与 a,b,ca,b,c 都相邻且 d∉Cd\notin C，那么 (a,c),(a,d)(a,c),(a,d) 必须在同一单元 C′C^{\prime} 中。由于 (a,b)(a,b) 已经在 CC 中所以 b∉C′b\notin C^{\prime}。那么 (b,c),(b,d)(b,c),(b,d) 必须在两个不同单元中且都不是 CC，矛盾。
引理 2：如果图 HH 是线图，那么：
(a) 图 HH 不存在与 K3,1K_{3,1}（即左部 33 个点、右部 11 个点的完全二分图，或者说 44 个点的”菊花图“）同构的子图；
(b) 如果图 HH 中存在两个共边的奇三角形 (a,b,c),(a,b,d)(a,b,c),(a,b,d)，那么 c∼dc\sim d，即 {a,b,c,d}\{a,b,c,d\} 的导出子图为 K4K_4。
(a) 的证明较为容易（其实这个思路在引理 1 的证明中已经出现）。假设存在 {a,b,c,d}\{a,b,c,d\}，满足 a∼b,a∼c,a∼d,b≁c,b≁d,c≁da\sim b,a\sim c, a\sim d,b\nsim c, b\nsim d, c\nsim d，那么 (a,b),(a,c),(a,d)(a,b),(a,c),(a,d) 三条边中任意两条在划分中显然不能属于同一单元，这就导致点 aa 在至少三个单元中。
(b) 容易由引理 1 得出。
事实上，这两个条件不仅是必要的，也是 HH 是线图的充要条件（证明见参考资料 1）。不过这一点不会在本文中用到。
考虑完共边奇三角形，再来看共边偶三角形：
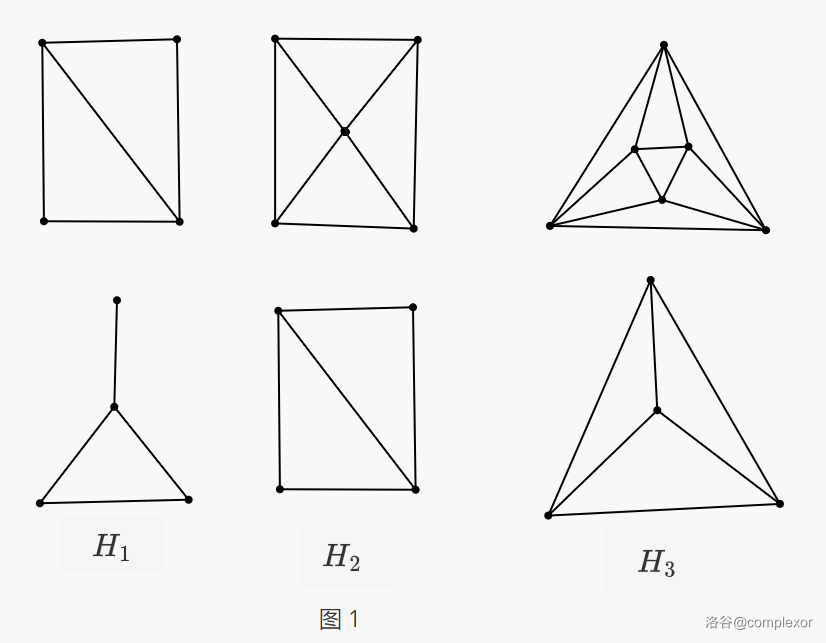
定理 2：如果线图 HH 中有两个共边的偶三角形 (a,b,c),(a,b,d)(a,b,c),(a,b,d)，那么 HH 在同构意义下只有三种可能（记为 H1,H2,H3H_1,H_2,H_3）。即如果线图 HH 不同构于 H1,H2,H3H_1,H_2,H_3，那么 HH 中任意两个共边三角形中至少一个是奇的。
容易验证 H1,H2,H3H_1,H_2,H_3 是线图（图 1 展示了这三种线图及他们的原图，线图在上，原图在下）
当图中只有 a,b,c,da,b,c,d 四个点时，对应的线图即为 H1H_1。
注意到如果 HH 的任一导出子图不满足引理 2 中的条件，那么 HH 一定也不满足，即 HH 不是线图。
所以可以用程序枚举所有不超过 77 个点的存在两个共边偶三角形的图，并通过引理 2 来验证，从而证明定理 2.
1
引理 3：在线图 HH 的划分中，设边 (a,b)(a,b) 所在单元为 CC，包含边 (a,b)(a,b) 的三角形为 (a,b,c1),(a,b,c2),…,(a,b,ck)(a,b,c_1),(a,b,c_2),\dots,(a,b,c_k)，那么 c1,c2,…,ckc_1,c_2,\dots,c_k 中至少有 k−1k-1 个在 CC 中。
证明类似引理 1，考虑反证：假设 c1,c2,…,cl(2≤l≤k)c_1,c_2,\dots, c_l(2\leq l \leq k) 均不在 CC 中，那么 (a,c1),(a,c2),…,(a,cl)(a,c_1),(a,c_2),\dots,(a,c_l) 需要在同一单元 CaC_a 中，(b,c1),(b,c2),…,(b,cl)(b,c_1),(b,c_2),\dots,(b,c_l) 需要在同一单元 CbC_b 中。由于 (a,b)(a,b) 在 CC 中，所以 Ca≠CbC_a\neq C_b 。但此时 Ca,CbC_a,C_b 都包含了边 (c1,c2)(c_1,c_2)，矛盾。
引理 4：如果图 HH 中的一个三角形在一个同构于 Kr(r≥4)K_r(r\geq 4) 的导出子图中，那么这个三角形是奇的。
正确性显然。
下面的定理为本文的算法提供了重要的思路和理论支撑：
定理 3：设线图 HH（不是 H1,H2,H3H_1,H_2,H_3）中边 (a,b)(a,b) 共在 k(k≥2)k(k\geq 2) 个三角形中，其中有 ll 个奇三角形 (a,b,c1),(a,b,c2),…,(a,b,cl)(a,b,c_1),(a,b,c_2),\dots,(a,b,c_l)，那么有：
(a) l=k−1l=k-1 或 l=kl=k；
(b) {a,b,c1,c2,…,cl}\{a,b,c_1,c_2,\dots,c_l\} 的导出子图一定是 HH 的划分中的一个单元。
(a) 由定理 2 容易证明。
(b) 是引理 1 的扩展，由引理 1 知 a,b,c1,c2,…,cla,b,c_1,c_2,\dots,c_l 一定在同一个单元中。由引理 4 知如果 l=k−1l=k-1，那么 {a,b,c1,c2,…,ck}\{a,b,c_1,c_2,\dots,c_k\} 的导出子图不可能是完全图，否则 (a,b,ck)(a,b,c_k) 应为奇三角形。而任何 x∉{a,b,c1,c2,…,ck}x\notin\{a,b,c_1,c_2,\dots,c_k\} 不能同时和 a,ba,b 有边，故也不在这个单元中。
下面描述了判断 HH 是否是线图并构造原图的算法，其中步骤 1,2 找到了一个单元，步骤 3 从这个单元开始构造了一个划分，步骤 4 通过划分构造原图 GG：
  1. 任取 HH 中一条边 (a,b)(a,b) 统计其所在的三角形数量，设为 kk：
    1. 若 k=0k=0，则 (a,b)(a,b) 一定为一个同构于 K2K_2 的单元，转到步骤 3；
    2. 若 k=1k=1，设该三角形为 (a,b,c)(a,b,c)。统计 (a,c),(b,c)(a,c),(b,c) 所在三角形数量若均为 11，则容易说明此时 HH 如果不是 K3K_3，则三角形 (a,b,c)(a,b,c) 一定一个单元，转到步骤 3。若 (a,c)(a,c) 在不小于 22 个三角形中，则用 (a,c)(a,c) 代替 (a,b)(a,b) 转到步骤 2，(b,c)(b,c) 同理；
    3. 若 k≥2k\geq 2，转到步骤 2。
  2. 统计 kk 个三角形中奇三角形个数，设为 ll，那么：
    1. 如果 k=2,l=0k = 2,l=0，此时 HH 可能为 H1,H2,H3H_1,H_2,H_3 或者不是线图，将其中任意三角形作为起始单元转到步骤 3（容易验证对于这三种图这样都能正确构造）；
    2. 否则如果 l<k−1l<k-1，由定理 3，HH 不为线图；
    3. 如果 l=kl=k 或 l=k−1l=k-1，那么由定理 3 也找到了一个单元，判断这个导出子图是否是完全图，转到步骤 3。
  3. 现在已经找到了划分中的一个单元 C1C_1，那么由于每个点至多在两个单元中，所以 C1C_1 中每个点 xx 如果有不在 C1C_1 中的边 (x,y1),(x,y2),…,(x,ys)(x,y_1),(x,y_2),\dots,(x,y_s)，那么 {x,y1,y2,…,ys}\{x,y_1,y_2,\dots,y_s\} 的导出子图一定是一个单元。一直这样递归下去，如果出现导出子图不是完全图或一个点出现在三个单元中，则 HH 不是线图。否则由 HH 连通，必然会将得到一个合法的划分。
  4. 得到划分后，为每个单元在 GG 中建一个点，并将这个点作为单元中每个点在 GG 中对应的边的一个端点。如果一个 HH 中的点只在一个划分中，则将 GG 中对应边的另一个端点设为一个仅与这条边相邻的新点。
步骤 1,2 精细实现可以做到 O(n+m)O(n+m) 的复杂度。步骤 3 中每个点只会访问不超过 33 次，故复杂度也可以做到 O(n+m)O(n+m)。步骤 4 容易做到 O(n+m)O(n+m)。
至此得到了一个 O(n+m)O(n+m) 复杂度的构造线图对应的原图的算法。
最后，对于 GG 可能存在重边的情况，设 AiA_i 为 ii 在 HH 中所有相邻点和 ii 自己构成的集合，那么将所有 AiA_i 相同的 ii 构造为重边，并对于每种 AiA_i 只保留这些 ii 中的一个，不难发现这样处理不改变答案的存在性。借助哈希容易以 O(n+m)O(n+m) 的复杂度完成。
总复杂度 O(n+m)O(n+m)。

参考资料

  1. van Rooij, A. C. M., & Wilf, H. S. 1965. "The interchange graph of a finite graph". Acta Mathematica, 16(3-4), 263–268.
  2. Roussopoulos, Nicholas D. 1973. "A max {m,n} Algorithm for Determining the Graph H from Its Line Graph G." Information Processing Letters 2 (4): 108-112.

评论

共 0 条评论，欢迎与作者交流。

正在加载评论...