专栏文章

小学生都能看懂的错排问题解析

PPlanet6174
P1595题解参与者 120已保存评论 148

文章操作

快速查看文章及其快照的属性，并进行相关操作。

当前评论
149 条
当前快照
1 份
快照标识符
@mhz5u0cp
此快照首次捕获于
2025/11/15 01:57
3 个月前
此快照最后确认于
2025/11/29 05:25
3 个月前
查看原文
点赞请戳屏幕右下角粉色的圆 QwQ
洛谷不支持 Flash 很蛋疼啊
我本来想做成交互式内容的，现在只能疯狂贴图……

你需要知道哪些信息学知识：

递推/简单DP。没了。

面向小学生的（并非严谨的）数学前置技能

  1. 数集：一堆的互不相同的数放在一起。
  2. 元素：数集中的一个数称为这个数集的一个元素。
  3. 数学上的函数：f(x)=f(x)= 表达式
    转化为信息学的写法长成这样：
CPP
double f(double x) {
     return 表达式;
}
  1. 一一对应：通俗的说法就是一个萝卜一个坑。
    数学上两个数集一一对应指的是：
    有两个数集 AA 和 BB，
    对于 AA 里面任意一个数，在 BB 中都能找到一个数与之对应；
    并且对于 BB 里面任意一个数，在 AA 中也一定能找到一个数与之对应，
    那么，数集 AA 与数集 BB 一一对应。

问题

有 nn 个箱子，颜色分别为 1…n1\dots n；还有 nn 个球，颜色也分别为 1…n1\dots n。现在要将每一个球分别放入一个箱子里，并且一个箱子里只能放一个球。
1.png
试求有多少种方案满足：每个箱子，和它里面球的颜色，都不一样。
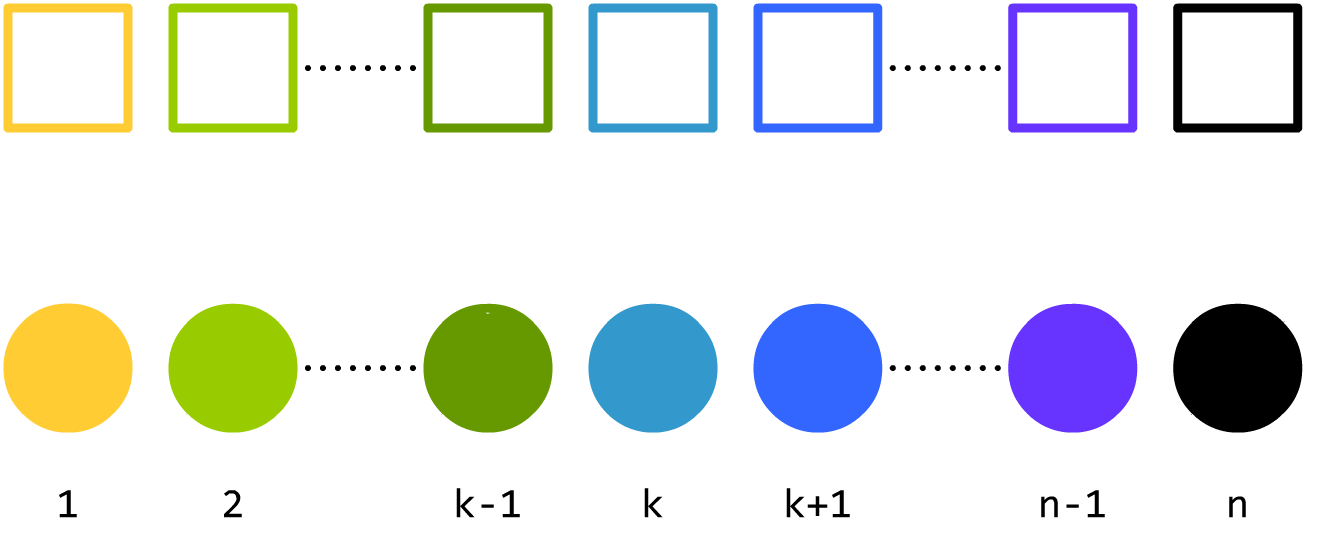
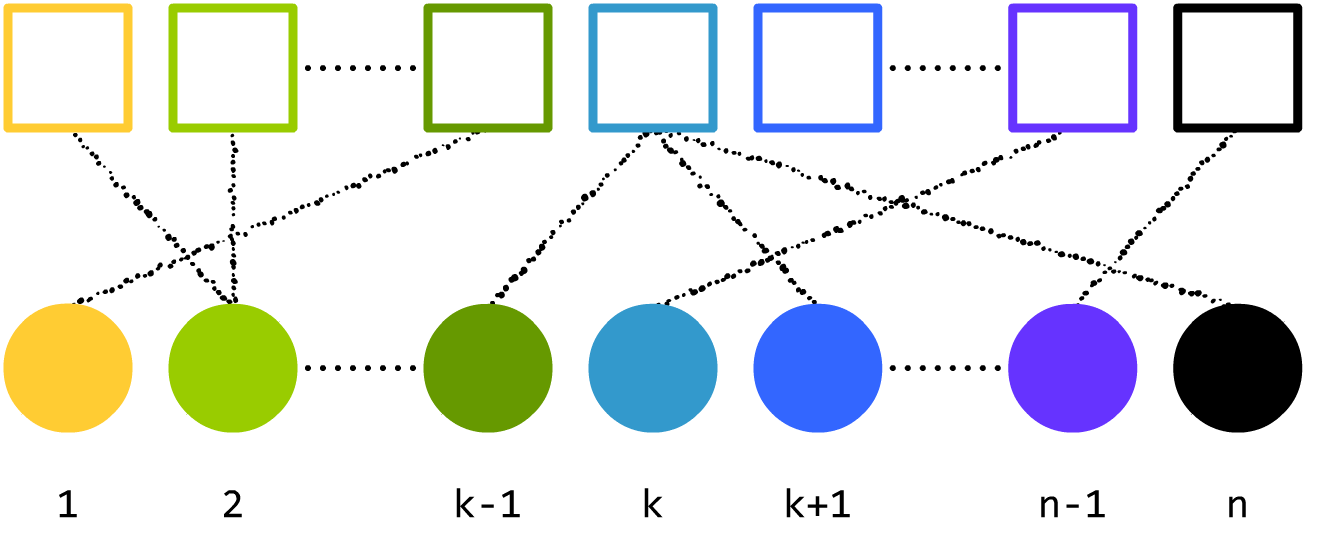
下图使用一种不知道叫啥的线表示哪个球不能放进哪个箱子里（再三强调不能放进，有些小盆友还以为是哪个球放哪个箱子里……）。后文还会多次出现这种不知道叫啥的线。
2.png
→→此处我们把 XX 号球 不能放进 YY 号箱称为一组对应关系，简写为 X∼YX\sim Y（注意，这不是书上正经的讲法和符号，这里这样写只是为了方便），画在图中就用这种不知道叫啥的线。←←
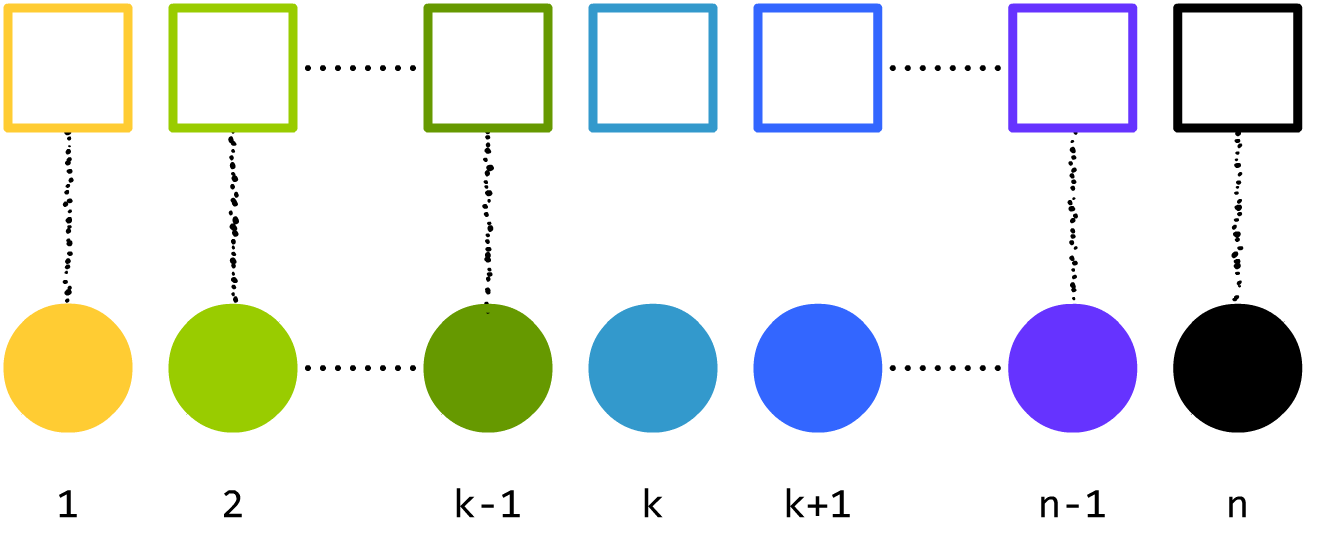
于是，我们换一种方式描述题目：试求有多少种方案满足：1∼11\sim 1，2∼22\sim 2，……，n∼nn\sim n。
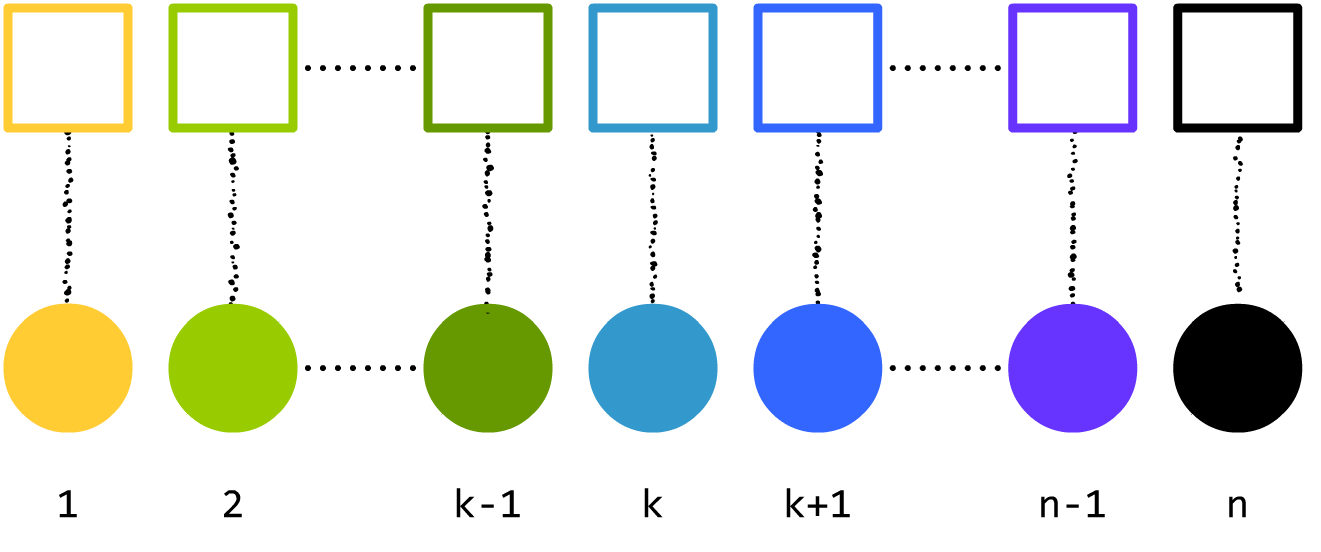
很多人学错排问题时，就只知道上面这种形式。然而，他们没有抓住错排问题的本质。我变一下，如果 1∼21\sim 2，2∼32\sim 3，……，n−1∼nn-1\sim n，n∼1n\sim 1，答案和上面一样吗？
3.png
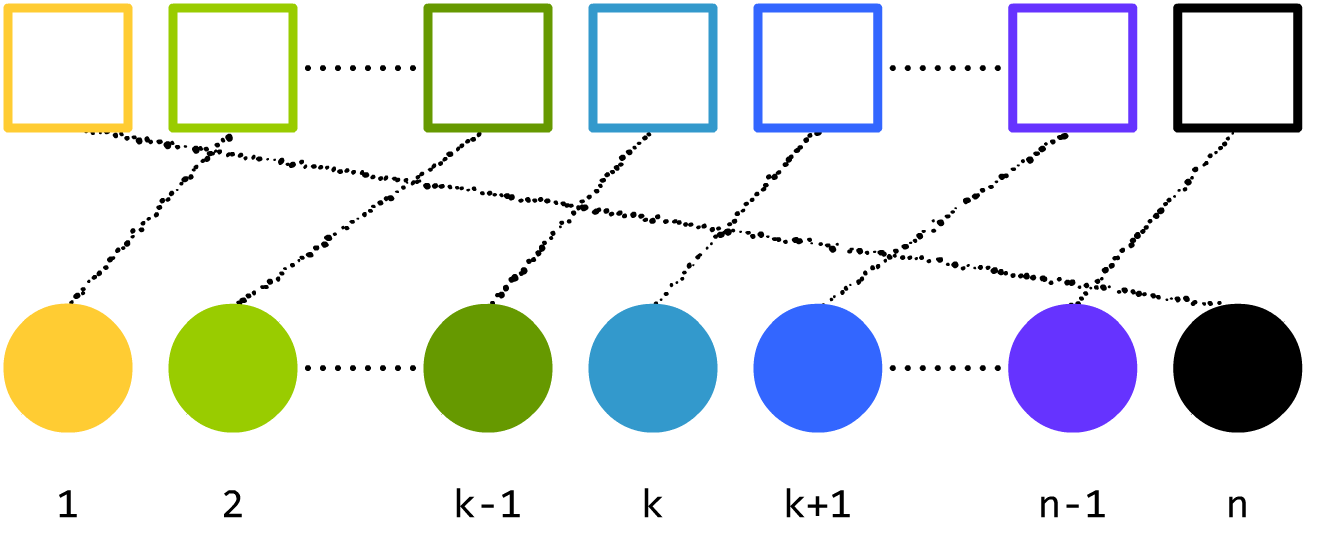
一样吧？那下面这种对应关系呢？
4.png
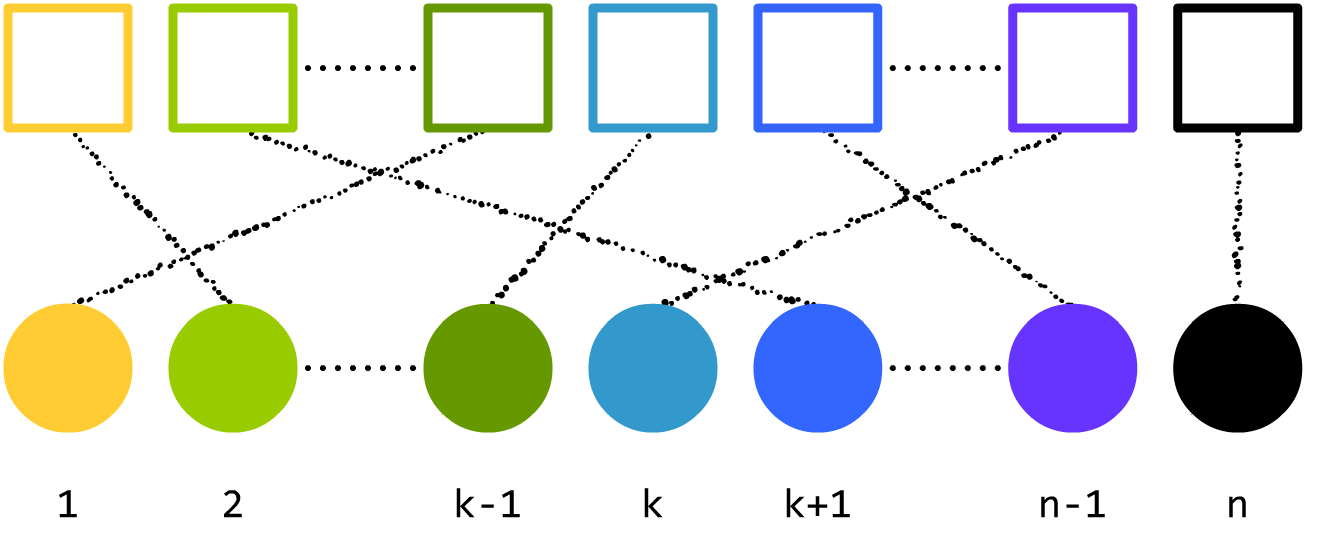
有点乱，但答案一样吧？但是，下面这几个呢？
5.png
6.png
看起来不对劲。前者出现了一对多、多对一，后者出现了有些球和箱子没有对应。没错，答案会不一样。
那么，你搞清楚了正确定义了吗？
 \
有 nn 个球，nn 个箱子。某个箱子不能放某一个球，其他球都可以放进去；反过来，某个球一定不能放进某个箱子，并且其他箱子都允许放进去。
现在要将每个球分别放进一个箱子里，一个箱子里只能放一个球。求方案数。
 \
现在，我们进入核心部分：

递推式

回到开头给的题目。
数学上我们用 DnD_n 表示有 nn 个球 nn 个箱子时的方案数。自己简单算一下可以得出 D1=0,D_1=0, D2=1,D_2=1, D3=2D_3=2。
我们来看下 Dn(n≥4)D_n(n\ge 4) 的情况。要推出怎么做，需要分类讨论。不妨分成 n−1n-1 种情况：nn 号球放进了 11 号箱子，nn 号球放进了 22 号箱子…… nn 号球放进了 n−1n-1 号箱子（现在我们在讲开头的题目，所以 nn 号球不能放进 nn 号箱子）。注意，分类讨论时要搞清楚是否涵盖了所有的情况。我们可以把所有情况列出来：
把 nn 号球放进：
  • 11 号箱子
  • 22 号箱子
  • ……
  • (k−1)(k-1) 号箱子
  • k\text{k} 号箱子
  • (k+1)(k+1) 号箱子
  • ……
  • (n−1)(n-1) 号箱子
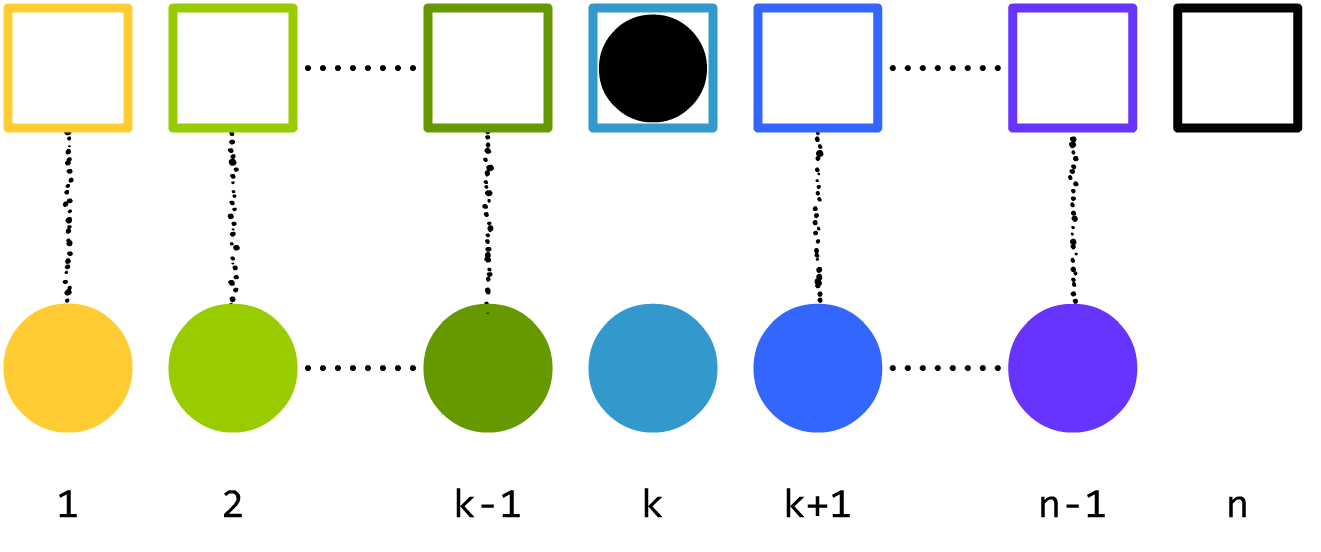
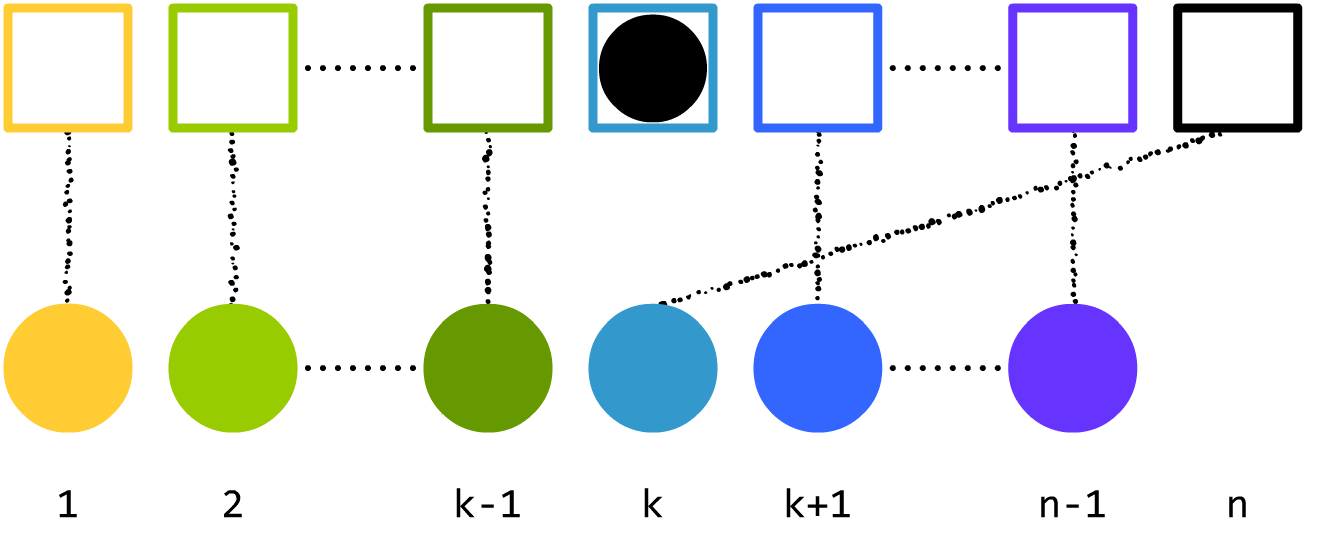
现在，我们只着眼于一种情况：nn 号球放进了 kk 号箱子。
7.png
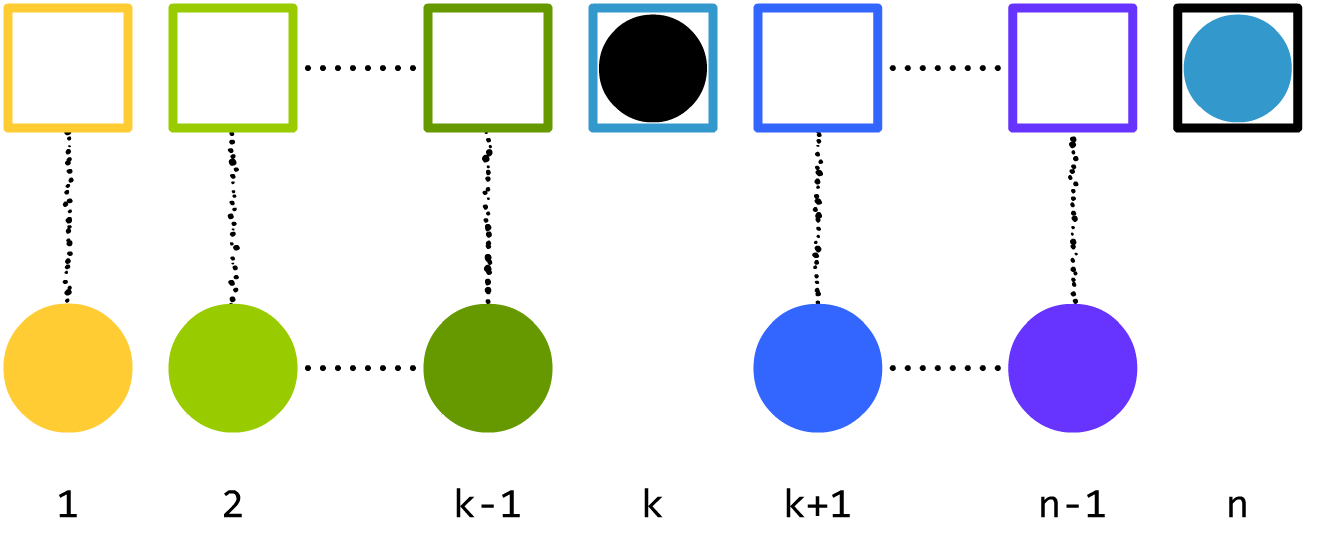
现在，我们再分为两种情况：一种是 kk 号球放进了 nn 号箱子，另一种是 kk 号球没有放进 nn 号箱子。
把 nn 号球放进：
  • 11 号箱子
  • 22 号箱子
  • ……
  • (k−1)(k-1) 号箱子
  • k\text{k} 号箱子
  • k\text{k} 号球放进了 n\text{n} 号箱子
  • k\text{k} 号球没有放进 n\text{n} 号箱子
  • (k+1)(k+1) 号箱子
  • ……
  • (n−1)(n-1) 号箱子
如果 kk 号球放进了 nn 号箱子：
8.png
我们可以发现，如果不看 kk 号球 kk 号箱子 nn 号球 nn 号箱子，那么，将剩下的球按规定放进剩下的箱子有 Dn−2D_{n-2} 种方案。
把 nn 号球放进：
  • 11 号箱子
  • 22 号箱子
  • ……
  • (k−1)(k-1) 号箱子
  • k\text{k} 号箱子
  • k\text{k} 号球放进了 n\text{n} 号箱子 ⟶\longrightarrow Dn−2D_{n-2} 种方案
  • k\text{k} 号球没有放进 n\text{n} 号箱子
  • (k+1)(k+1) 号箱子
  • ……
  • (n−1)(n-1) 号箱子
 \
为了和上面区分，这里我们描述为：如果 kk 号球不能放进 nn 号箱子。
动脑筋想想，这个东西是不是可以写成 k∼nk\sim n？（回到上面读读 ∼\sim 的定义）
9.png
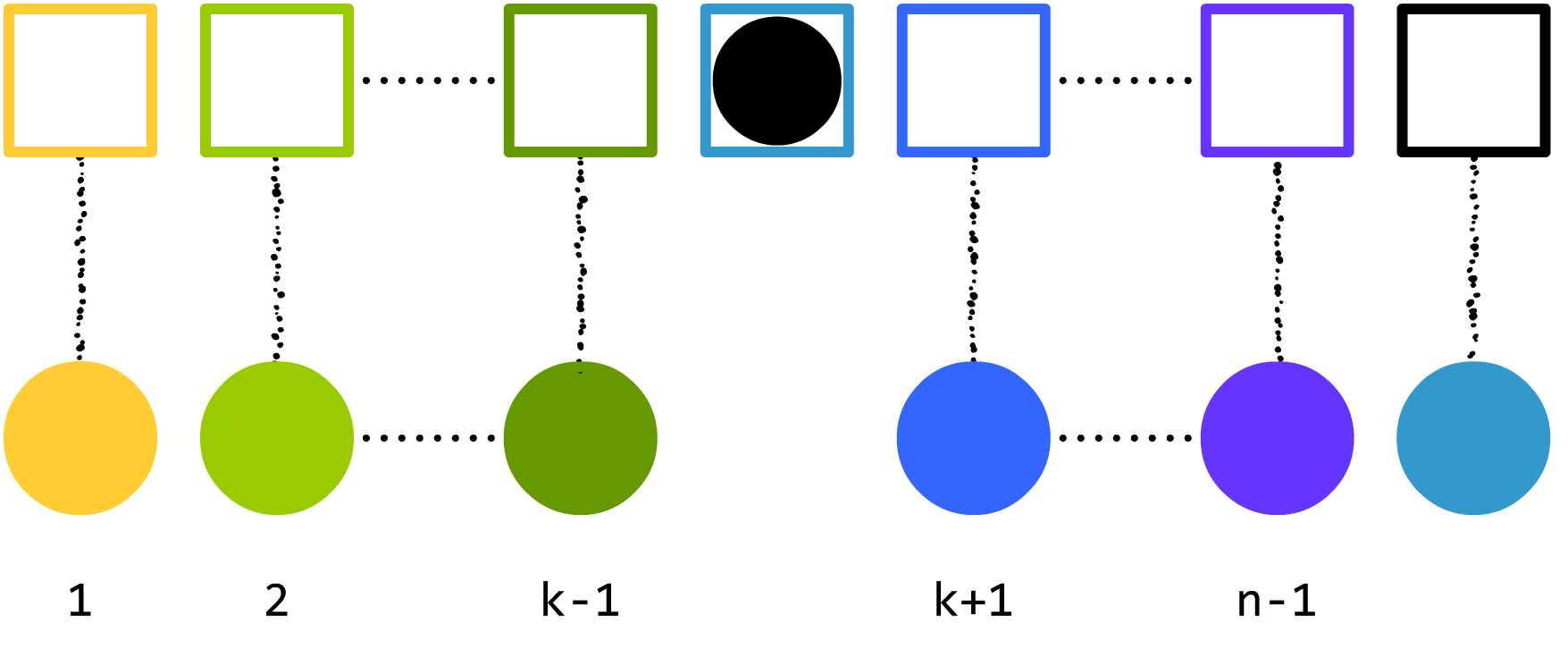
我们可以发现，如果不看 nn 号球和 kk 号箱子，那么，将剩下的球按规定放进剩下的箱子有 Dn−1D_{n-1} 种方案。还没看懂？那我把 kk 号球移过来，你能不能看懂？
10.png
还没看懂？回到上面读读错排问题的正确定义。
把 nn 号球放进：
  • 11 号箱子
  • 22 号箱子
  • ……
  • (k−1)(k-1) 号箱子
  • k\text{k} 号箱子
  • k\text{k} 号球放进了 n\text{n} 号箱子 ⟶\longrightarrow Dn−2D_{n-2} 种方案
  • k\text{k} 号球没有放进 n\text{n} 号箱子 ⟶\longrightarrow Dn−1D_{n-1} 种方案
  • (k+1)(k+1) 号箱子
  • ……
  • (n−1)(n-1) 号箱子
 \
我们发现，把 nn 号球放进 k\text{k} 号箱子后的两种情况我们都能够求出答案。现在，我们可以把两者合起来！
把 nn 号球放进：
  • 11 号箱子
  • 22 号箱子
  • ……
  • (k−1)(k-1) 号箱子
  • k\text{k} 号箱子 ⟶\longrightarrow Dn−2+Dn−1D_{n-2}+D_{n-1} 种方案
  • k\text{k} 号球放进了 n\text{n} 号箱子 ⟶\longrightarrow Dn−2D_{n-2} 种方案
  • k\text{k} 号球没有放进 n\text{n} 号箱子 ⟶\longrightarrow Dn−1D_{n-1} 种方案
  • (k+1)(k+1) 号箱子
  • ……
  • (n−1)(n-1) 号箱子
这个 kk 是一个未知数，也就是说，无论 k=1k=1 还是 22 还是多少，答案是不变的！
把 nn 号球放进：
  • 11 号箱子 ⟶\longrightarrow Dn−2+Dn−1D_{n-2}+D_{n-1} 种方案
  • 22 号箱子 ⟶\longrightarrow Dn−2+Dn−1D_{n-2}+D_{n-1} 种方案
  • ……
  • (k−1)(k-1) 号箱子 ⟶\longrightarrow Dn−2+Dn−1D_{n-2}+D_{n-1} 种方案
  • k\text{k} 号箱子 ⟶\longrightarrow Dn−2+Dn−1D_{n-2}+D_{n-1} 种方案
  • (k+1)(k+1) 号箱子 ⟶\longrightarrow Dn−2+Dn−1D_{n-2}+D_{n-1} 种方案
  • ……
  • (n−1)(n-1) 号箱子 ⟶\longrightarrow Dn−2+Dn−1D_{n-2}+D_{n-1} 种方案
最后一步，你会了吗？
 \
D1=0\large D_1=0 D2=1\large D_2=1 Dn=(n−1)(Dn−1+Dn−2)(n≥2)\large D_n=(n-1)(D_{n-1}+D_{n-2})(n\ge 2)

通项公式

下面这些我没有和小学生讲，错排的通项公式对小学生还是太难了一点。
Dn=n![12!−13!+⋯+(−1)n1n!]D_n=n!\left[\frac{1}{2!}-\frac{1}{3!}+\dots+(-1)^n\frac{1}{n!}\right]
还有一个原因，这东西没法子快速计算……
顺便讲一下这东西怎样从递推式推导为通项公式的。以下内容来自维基。
设 Dn=n!MnD_n = n!M_n，则 M1=0,M2=12M_1 = 0, M_2 = \dfrac {1}{2}。 当 n≥3n\ge 3 时，Dn=(n−1)(Dn−1+Dn−2)D_n = (n-1)(D_{n-1} + D_{n-2})，即 n!Mn=(n−1)×(n−1)!Mn−1+(n−1)×(n−2)!Mn−2=n!Mn−1−(n−1)!Mn−1+(n−1)!Mn−2n!M_{n}=(n-1)\times (n-1)!M_{n-1}+(n-1)\times (n-2)!M_{n-2}=n!M_{n-1}-(n-1)!M_{n-1}+(n-1)!M_{n-2} 化简得 nMn−nMn−1=−Mn−1+Mn−2nM_{n}-nM_{{n-1}}=-M_{{n-1}}+M_{{n-2}}
于是 Mn−Mn−1=−1n(Mn−1−Mn−2)=...=(−1n)(−1n−1)...(−13)(M2−M1)=(−1)n1n!M_{n}-M_{{n-1}}=-{\frac {1}{n}}(M_{{n-1}}-M_{{n-2}})=...=(-{\frac {1}{n}})(-{\frac {1}{n-1}})...(-{\frac {1}{3}})(M_{2}-M_{1})=(-1)^{n}{\frac {1}{n!}} 所以 Mn−Mn−1=(−1)n1n!Mn−1−Mn−2=(−1)(n−1)1(n−1)!⋮=⋮M2−M1=(−1)212!\begin{aligned}M_{{n}}-M_{{n-1}}&=(-1)^{{n}}{\frac {1}{n!}}\\M_{{n-1}}-M_{{n-2}}&=(-1)^{{(n-1)}}{\frac {1}{(n-1)!}}\\\vdots \quad &=\quad \vdots \\M_{2}-M_{1}&=(-1)^{2}{\frac {1}{2!}}\\ \end{aligned} 将上面式子分边累加，得 Mn=(−1)212!+(−1)313!...+(−1)n1n!M_{n}=(-1)^{2}{\frac {1}{2!}}+(-1)^{3}{\frac {1}{3!}}...+(-1)^{{n}}{\frac {1}{n!}} 因此，我们得到错排的通项公式 Dn=n!Mn=n![12!−13!+...+(−1)n1n!]D_{n}=n!M_{n}=n!\left[{\frac {1}{2!}}-{\frac {1}{3!}}+...+(-1)^{n}{\frac {1}{n!}}\right]

评论

共 148 条评论，欢迎与作者交流。

正在加载评论...