专栏文章
题解:P12448 [COTS 2025] 观草 / Trava
P12448题解参与者 9已保存评论 20
文章操作
快速查看文章及其快照的属性,并进行相关操作。
- 当前评论
- 20 条
- 当前快照
- 1 份
- 快照标识符
- @mint0vkb
- 此快照首次捕获于
- 2025/12/02 07:52 3 个月前
- 此快照最后确认于
- 2025/12/02 07:52 3 个月前
题目:观草。
观观草草,草草观观,草观草观草。观草观草,草观草观,观草观草观。
请注意,这并不是一首有名的诗歌。
Part 0
当求和本身不好计算的时候,我们应该考虑 能产生的贡献。
于是研究 对长度 的区间的贡献次数。
从 开始往两边拓展,若拓展到比它大的数,区间最大值就不是它了,此时终止拓展。右侧同理。
PICTURE
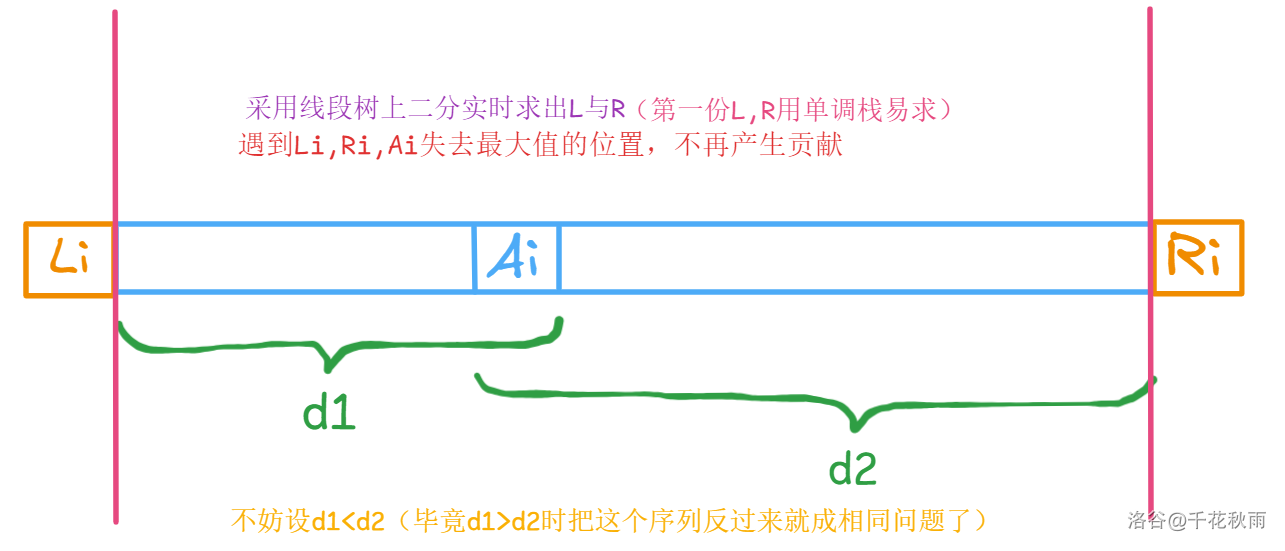
:左边最近的,严格大于 的元素位置,没有则 。:找右边最近的,大于等于 的元素位置,没有则 。计算需求,我们钦定同样大小的数字,位置越右边的越大。
对于区间 ,从 开始往左的可拓展距离 为 。从 开始往右的可拓展距离 为 。
Info
:即 ,共 个数。
:即 ,共 个数。
题外话:这里的初始 我用单调栈算,是因为我的单调栈和线段树查询有点不一样,如果修改合适可以直接线段树二分求答案。
Part 1
当区间长度 ,此时区间起点可以从 一直到 。
为什么到了 不能再往右了?
因为我们求的是 对长度 的区间的贡献次数。自然这个区间必须包含 。
PICTURE
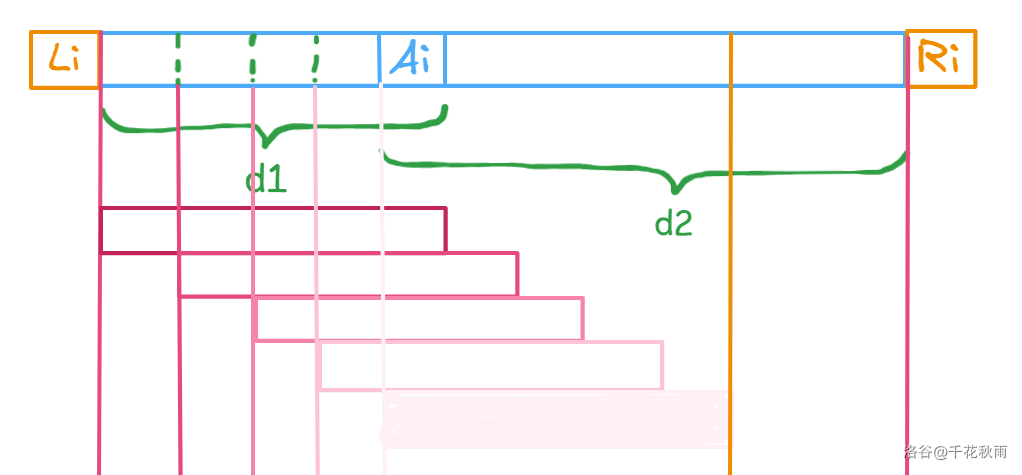
,以 开头往右走还有 的距离,所以可以保证 这一段不会碰到 。
所以贡献次数等于可能区间起点数,也就是 ,共 个数。
Part 2
当区间长度 。起点可以是 的任意一个。
因为超过 的覆盖长度保证了从这些起点开始一定盖的住 。并且不会超出右侧 的限制。
PICTURE

和上面一样的,到了 不能再往右是因为这个区间必须包含 。不然就不是 做的贡献了。
此时总贡献次数为 。
Part 3
。
个数取决于区间长度。我们终点从 开始,往左延申起点。
PICTURES
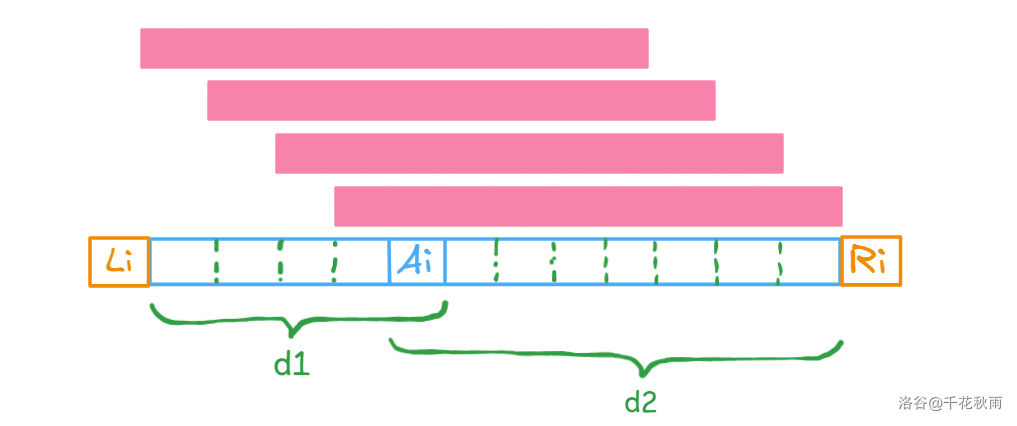
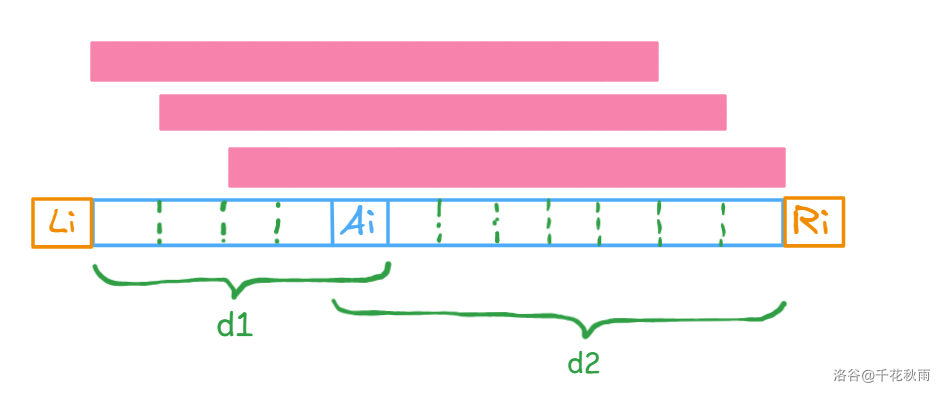
不难发现 与可行区间个数有关联。
- 。
- 。
- 。
省流
- ,贡献次数 。
- ,贡献次数 。
- ,贡献次数 。
CODE
code
CPP#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define For(i,L,R) for(int i=L;i<=R;i++)
#define lc u<<1
#define rc u<<1|1
const int N=5e5+10;
int n,m,a[N];
int stk[N],top;
int L[N],R[N];
int t[N<<2];
void pushup(int u){
t[u]=max(t[lc],t[rc]);
}
void build(int u,int L,int R){
if(L==R){
t[u]=a[L];
return;
}
int m=(L+R)>>1;
build(lc,L,m);
build(rc,m+1,R);
pushup(u);
}
void upd(int u,int L,int R,int p,int v){
if(L==R){t[u]+=v;return;}
int m=(L+R)>>1;
if(p<=m)upd(lc,L,m,p,v);
else upd(rc,m+1,R,p,v);
pushup(u);
}
int fl(int u,int L,int R,int l,int r,int v){
if(t[u]<v||l>r)return -1;
if(L==R)return L;
int m=(L+R)>>1,res=-1;
if(l<=m)res=fl(lc,L,m,l,r,v);
if(res==-1&&r>m)res=fl(rc,m+1,R,l,r,v);
return res;
}
int fr(int u,int L,int R,int l,int r,int v){
if(t[u]<v||l>r)return -1;
if(L==R)return L;
int m=(L+R)>>1,res=-1;
if(r>m)res=fr(rc,m+1,R,l,r,v);
if(res==-1&&l<=m)res=fr(lc,L,m,l,r,v);
return res;
}
ll k[N],d[N];
void add(int x,ll vk,ll vd){
for(;x<=n;x+=x&-x){
k[x]+=vk;
d[x]+=vd;
}
}
void work(int L,int R,ll vk,ll vd){
if(L>R)return;
add(L,vk,vd);
add(R+1,-vk,-vd);
}
pair<ll,ll>qry(int x){
ll sk=0,sd=0;
for(;x;x-=x&-x){sk+=k[x];sd+=d[x];}
return make_pair(sk,sd);
}
void upr(int u,int lp,int rp,ll x){
int d1=u-lp,d2=rp-u,t=rp-lp-1;
if(d1>d2)swap(d1,d2);
work(1,d1,x,0);
if(d1<d2)work(d1+1,d2,0,d1*x);
if(d2<t)work(d2+1,t,-x,(t+1)*x);
}
ll solve(int u){
pair<ll,ll>p=qry(u);
return p.first*u+p.second;
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
cin>>n>>m;
For(i,1,n){
cin>>a[i];
while(top&&a[stk[top]]<=a[i]){
R[stk[top--]]=i;
}
L[i]=stk[top];
stk[++top]=i;
}
while(top){
R[stk[top--]]=n+1;
}
For(i,1,n){
upr(i,L[i],R[i],a[i]);
}
build(1,1,n);
while(m--){
char op;int k;
cin>>op>>k;
if(op=='?')cout<<solve(k)<<"\n";
else{
a[k]++;
upd(1,1,n,k,1);
int l=fr(1,1,n,1,k-1,a[k]);
if(l==-1)l=0;
int r=fl(1,1,n,k+1,n,a[k]);
if(r==-1)r=n+1;
upr(k,l,r,1);
}
}
return 0;
}
相关推荐
评论
共 20 条评论,欢迎与作者交流。
正在加载评论...