前言

众所不周知，一篇文章应该有一张头图。

2025 年 12 月，笔者发表了《再谈铲雪》。这篇文章写的依托，因此选择重构。

本文主要更新如下：

解决了基环树铲雪；
增加了使用笛卡尔树解决序列铲雪的方法；
增加了利用线性规划解决一般铲雪问题的方法；
补充了若干铲雪相关例题；
对全文结构进行了重新梳理；
新增配套题单。

如果写的还是很烂，欢迎在评论区开骂。

约定

在转移式中出现 $f_{0/1,i}$ 这样的表达式时，实际表示 $\max(f_{0,i},f_{1,i})$ 。
参考代码中默认使用 #define int long long。

铲雪模型

首先给出铲雪问题的一个基础形式：

给定无向图 $G$ ，每个点具有非负整数值点权 $a_i$ 。每次操作可将某个特定结构上的所有点权减 $1$ ，且操作过程中点权不能为负。

求使所有点权变为 $0$ 的最小操作次数。

下文将分别针对

G

为链、环、树、基环树的情形给出多种解法，并附上一些相似类型的题目。

1. 前置知识

1.1 差分

相信大家都会。

1.2 笛卡尔树

笛卡尔树

模板题：P5854。

笛卡尔树是一棵二叉树，每个节点有权值二元组

(i,a_i)

，要求下标

i

满足二叉搜索树性质，权值

a_i

满足堆性质。

笛卡尔树可在

O(n)

时间内构建。顺序插入每个

a_i

，可知新节点一定位于当前根的右链上。自底向上比较右链节点的权值，若满足偏序关系，则将新节点挂为右子，原右子树变为其左子树。可用单调栈维护右链。参考代码：

CPP

int n, a[N], l[N], r[N];
void build() {
    stack<int> st;
    for (int i = 1; i <= n; i++) {
        while (!st.empty() && a[st.top()] > a[i]) l[i] = st.top(), st.pop();
        if (!st.empty()) r[st.top()] = i;
        st.emplace(i);
    }
}

笛卡尔树可视为一种分治结构：找到当前区间最大值，然后从最大值两段劈开继续递归。

在铲雪问题中，我们利用的正是这种基于最小值的分治特性，并可在笛卡尔树上进行 DP 来实现

O(n)

复杂度。

1.3 对偶原理

线性规划与对偶

我们称一个线性规划问题的标准形式形如

\begin{aligned} \min & \sum _{i=1}^n c_i x_i\\ \text{subject to } & \sum_{j=1}^n a_{i,j} x_j \le b_i, i=1,\cdots,m\\ & x_i \ge 0, i = 1, \cdots, n. \end{aligned}

用自然语言描述，就是找到

n

个非负实数

x_i

，同时给出

m

条形如

\sum \limits_{j=1}^n a_{i,j} x_j \le b_i

的约束，要求最小化

\sum \limits_{i=1}^n c_i x_i

。

称以上问题的对偶问题为

\begin{aligned} \max & \sum _{i=1}^m b_i y_i\\ \text{subject to } & \sum_{j=1}^m a_{j,i} x_j \ge c_i, i=1,\cdots,n\\ & y_i \ge 0, i = 1, \cdots, m. \end{aligned}

也就是

b_i,c_i

互换，系数矩阵转置，然后小于号变成大于号。

对于一般的线性规划，有强对偶定理：线性规划问题的解与其对偶问题的解相等，只要原问题或对偶问题之一可行。

铲雪问题的对偶

对于普通铲雪，我们总是能得到这样一个线性规划：设集簇

\mathcal I

表示所有合法路径，对每条路径

S

给出一个非负整数

x_S

表示

S

被经过的次数，原问题即：

\begin{aligned} \min & \sum _{S \in \mathcal{I}} x_S\\ \text{subject to } & \sum_{u \in S} x_S=a_u, \\ & x_S \ge 0. \end{aligned}

拆成不等式以得到标准形式：

\begin{aligned} \min & \sum _{S \in \mathcal{I}} x_S\\ \text{subject to } & \sum_{u \in S} x_S \ge a_u, \\ & \sum_{u \in S} -x_S \ge -a_u, \\ & x_S \ge 0. \end{aligned}

得到对偶问题

\begin{aligned} \max & \sum _{u} a_u(p_u-q_u)\\ \text{subject to } & \sum_{u \in S} (p_u-q_u) \le 1, \\ & p_u,q_u \ge 0. \end{aligned}

换元，令

w_u=p_u-q_u

，问题变为

\begin{aligned} \max & \sum _{u} a_uw_u\\ \text{subject to } & \sum_{u \in S} w_u \le 1. \end{aligned}

用自然语言表述这个问题，相当于找到一组整数

w_u

，对所有满足条件的路径，

w_u

之和不大于

1

，最大化

a_uw_u

的和。

这个问题有一个比较通用的 DP 做法。

2. 序列铲雪

P1969 [NOIP 2013 提高组] 积木大赛。

给定序列 $a_i$ ，每次操作可将一个区间内的所有元素减 $1$ ，且操作过程中元素值不能为负。

求使所有元素变为 $0$ 的最小操作次数。

请读者重视这道题目。下面给出的四种方法都是解决铲雪题的常用思路。

2.1 差分法

用差分刻画操作。约定

a_0=a_{n+1}=0

，令

d_i=a_i-a_{i-1}

，则：

对区间 $[l,r]$ 的操作等价于 $d_l \gets d_l+1,\ d_{r+1} \gets d_{r+1}-1$ 。
目标状态为 $\forall 1 \le i \le n,\ d_i=0$ 。

注意到

\sum \limits_{i=1}^{n+1} d_i = 0

，因此操作总是可行的。进一步，每个正差分必然与某个负差分配对，因此答案至少为所有正差分之和。

若将所有正差分消为

0

后仍不合法，则与可行性矛盾。故答案为：

\sum_{i=1}^n \max(0,d_i)=\dfrac{1}{2} \sum_{i=1}^{n+1} |d_i|

这是一个经典结论。等号两侧的式子是等价的，两种形式在后续问题中均有用到。

CPP

int n, a[N];
void _main() {
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i];
    int res = 0;
    for (int i = 1; i <= n; i++) res += max(0LL, a[i] - a[i - 1]);
    cout << res;
}

2.2 插头法

插头是铲雪题里一个重要的概念。在本题中，我们定义一个插头为一条可以向左右延伸的操作区间。

假设已处理完左侧，当前位于位置

i

，左侧传来的右插头数量为

k

，则：

若 $k \ge a_i$ ，则全部使用这些插头，并生成 $a_i$ 个新的右插头；
若 $k < a_i$ ，则使用全部插头后还需额外进行 $a_i-k$ 次操作，并生成 $a_i$ 个新的右插头。

不难发现这个过程和差分法得到的结论是等价的。

CPP

int n, a[N];
void _main() {
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i];
    int res = 0, k = 0;
    for (int i = 1; i <= n; i++) {
        if (k < a[i]) res += a[i] - k;
        k = a[i];
    } cout << res;
}

2.3 笛卡尔树法

这个方法基于一个观察：每次操作应尽量选择更长的区间。

考虑区间

[l,r]

，我们希望每次操作都能覆盖整个区间。这样的操作次数有一个上界，即区间最小值

a_x

。

设区间最小值为

a_x

，可将

[l,r]

中每个数减去

a_x

，此时

a_x

变为

0

，不能再参与操作。之后递归处理

[l,x-1]

与

[x+1,r]

。

形式化地，设

f(l,r,v)

表示区间

[l,r]

在已减去

v

的基础上还需的最小操作次数，则有：

f(l,r,v)=f(l,x-1,v+a_x)+a_x-v+f(x+1,r,v+a_x)

使用普通的 RMQ 可以做到

O(n \log n)

。注意到这是一个“按照最小值分裂区间”的分治结构，小根笛卡尔树上 DP 即可做到

O(n)

。

CPP

int n, a[N], rt, l[N], r[N], ans;
void build() {
    stack<int> st;
    for (int i = 1; i <= n; i++) {
        while (!st.empty() && a[st.top()] > a[i]) l[i] = st.top(), st.pop();
        if (!st.empty()) r[st.top()] = i;
        else rt = i;
        st.emplace(i);
    }
}
void dfs(int u) {
    if (l[u]) ans += a[l[u]] - a[u], dfs(l[u]);
    if (r[u]) ans += a[r[u]] - a[u], dfs(r[u]);
}
void _main() {
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i];
    build();
    ans += a[rt], dfs(rt), cout << ans;
}

2.4 线性规划法

考虑对偶问题：找到一组整数

w_i

，对所有区间

w_i

之和不大于

1

，最大化

a_iw_i

的和。

显然

w_i \le 1

。同时

w_i \le -2

是无意义的，因为它并不能抵消掉

w_i=1

的影响。因此

w_u \in \{-1,0,1\}

。

借鉴 2.2 的插头思想，定义一个插头为延伸到当前位置的最大 $w_i$ 和。注意这里的插头概念不同，请注意区分。

考虑顺序扫描 DP。对于

i

位置的决策，有如下四种情况：

选择 $w_i=-1$ ，右插头为 $0$ 。
选择 $w_i=0$ ，右插头为 $0$ 。
选择 $w_i=0$ ，右插头为 $1$ 。
选择 $w_i=1$ ，右插头为 $1$ 。

设计 DP 状态为

f_{0/1/2/3,i}

表示

i

位置的决策是第

0/1/2/3

种情况时，前缀

[1,i]

的最大得分。则容易写出转移：

\begin{aligned} f_{0,i}&=-a_i+f_{0/1/2/3,i-1}\\ f_{1,i}&=f_{0/1,i-1}\\ f_{2,i}&=f_{2/3,i-1}\\ f_{3,i}&=a_i+f_{0/1,i-1} \end{aligned}

答案为

f_{0/1/2/3,n}

。

CPP

int n, a[N], f[4][N];
void _main() {
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i];
    for (int i = 1; i <= n; i++) {
        f[0][i] = -a[i] + max({f[0][i - 1], f[1][i - 1], f[2][i - 1], f[3][i - 1]});
        f[1][i] = max(f[0][i - 1], f[1][i - 1]);
        f[2][i] = max(f[2][i - 1], f[3][i - 1]);
        f[3][i] = a[i] + max(f[0][i - 1], f[1][i - 1]);
    } cout << max({f[0][n], f[1][n], f[2][n], f[3][n]});
}

事实上，对于序列铲雪，我们有更强的结论：存在一个最优解，使得

w_i

除

0

外

1,-1

交替。但是上面给出的 DP 是通用的方法，请读者务必理解。

3. 环上铲雪

AT_arc136_c [ARC136C] Circular Addition。

给定环 $a_i$ ，每次操作可将一个区间（或整个环）上的所有元素减 $1$ ，且操作过程中元素值不能为负。

求使所有元素变为 $0$ 的最小操作次数。

3.1 差分法

用环上差分刻画操作。设

d_i=a_i-a_{i-1}

，特别地

d_1=a_1-a_n

。

注意到序列铲雪的结论

D=\dfrac{1}{2} \sum \limits_{i=1}^n |d_i|

，这是答案的一个下界，因为一次操作至多让

D

减去

1

，而目标是

D \gets 0

。

但是由于环的特殊结构，只考虑

D

会导致存在

a_i >0

，如样例 #3。注意到另外一个下界：

M=\max \limits_{i=1}^n a_i

。

给出一个引理：当环中存在

0

时，必有

M<D

。
证明：因为

D \ge \max \limits_{i=1}^n a_i-\min \limits_{i=1}^n a_i

，后一项为

0

时

D \ge M

，矛盾。

下面的充分性证明可能比较抽象，建议自己举一些例子来理解。

当 $M=D$ 时，环中不存在 $0$ ，选择一个最小的包含了所有最大值的区间即可令 $M \gets M-1,D \gets D-1$ 。
当 $M > D$ 时，环中不存在 $0$ ，对整环操作即可令 $M \gets M-1$ ， $D$ 至多减去 $1$ 。可以规约到 $M=D$ 的情况。
当 $M < D$ 时，选择一个全为最大值的极长区间，则 $D \gets D-1$ ， $M$ 至多减去 $1$ 。同样规约到 $M=D$ 的情况。

因此，我们证明了答案为

\max(M,D)

的充分性。

3.2 插头法

根据 2.2 的“尽量使用已有插头”思想，我们找一个位置断环为链以后，顺序扫描序列，初始时认为有

a_1

个插头。

根据贪心思想，我们应该从最小值处断环为链。

本题的特殊性为存在“整环”这一类操作，而 2.2 的做法无法区分链头的插头属于环还是区间。

为此，我们记录

A

为从

1

开始的插头数目，

B

为有潜力延伸到

1

的插头数目，

C

为其它类型的插头数目。如下决策：

若 $a_i<a_{i+1}$ $a_{i} < a_{i + 1}$ ，此时新产生 $d=a_{i+1}-a_i$ $d = a_{i + 1} - a_{i}$ 个插头，我们希望其尽量归入 $B$ $B$ 。
- 对于 $B$ 的变化量 $\Delta B$ ，显然有 $\Delta B \le d$ 。
- 新的插头和已有的 $B$ 类插头数之和不能超过用过的 $A$ 类插头数目。即 $\Delta B \le a_1-A-B$ 。
- 两个上界取 $\min$ ，剩余插头归入 $C$ 类。
- 令 $B \gets B + \Delta B$ ， $C \gets C+d-\Delta B$ ，同时支付 $d$ 的代价。
若 $a_i>a_{i+1}$ ，则可以用 $d=a_i-a_{i+1}$ 个插头。此时希望尽量保护 $B$ 类插头，故按 $A,C,B$ 的顺序使用插头。

最终答案加上

a_1

，再减去

B

个与

a_1

形成整环的操作。

CPP

#define int long long
const int N = 2e5 + 5;
int n, a[N];
void S(int& x, int& y) {
    int d = min(x, y);
    x -= d, y -= d;
}

void _main() {
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i];
    rotate(a + 1, min_element(a + 1, a + n + 1), a + n + 1);
    int A = a[1], B = 0, C = 0, res = 0;
    for (int i = 1; i < n; i++) {
        if (a[i] < a[i + 1]) {
            int d = a[i + 1] - a[i];
            int nB = min(d, max(0LL, a[1] - A - B));
            B += nB, C += d - nB, res += d;
        } else if (a[i] > a[i + 1]) {
            int d = a[i] - a[i + 1];
            S(A, d), S(C, d), S(B, d);
        }
    } cout << res + a[1] - B;
}

3.3 线性规划法

对偶问题的约束在环上更强：起点与终点的插头不能同时为

1

。

任意找一个点断环为链，做一次 2.4 的线性 DP。我们只需钦定终点的右插头为

0

，即可防止起终点的插头同时为

1

的情况。而如果钦定终点的插头为

1

，则需要起点插头为

0

，只需要倒着 DP 一遍。

考虑一个特殊情况：存在唯一

i

使得的

w_i=1

，其余全选

0

，此时起终点的插头同时为

1

但合法，这种情况的最大得分就是

\max \limits_{i=1}^n a_i

。需要加上这个特判。

CPP

int n, a[N], f[4][N];
void _main() {
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i];
    int res = *max_element(a + 1, a + n + 1);
    auto work = [&]() -> void {
        for (int i = 1; i <= n; i++) {
            f[0][i] = -a[i] + max({f[0][i - 1], f[1][i - 1], f[2][i - 1], f[3][i - 1]});
            f[1][i] = max(f[0][i - 1], f[1][i - 1]);
            f[2][i] = max(f[2][i - 1], f[3][i - 1]);
            f[3][i] = a[i] + max(f[0][i - 1], f[1][i - 1]);
        } 
        res = max({res, f[0][n], f[1][n]});
    };
    work(), reverse(a + 1, a + n + 1), work();
    cout << res;
}

4. 树上铲雪

P7246 手势密码。

给定一棵树，点权为 $a_i$ ，每次操作可将一条树链上的所有点权减 $1$ ，且操作过程中点权不能为负。

求使所有点权变为 $0$ 的最小操作次数。

4.1 插头法

定义一个插头为一条可以向祖先 / 兄弟延伸的操作。对于节点

u

，要求其所有儿子已处理完毕且点权清零。

设

f_u

为

u

节点的插头数目，记

s_u = \sum \limits_{v \in \operatorname{son(u)}} f_v

。

来自不同儿子、延伸至同一节点的两个插头有两种处理方式：在

u

处合并，或继续向上延伸。设

c_u

为

u

节点处线头合并次数，则它对答案的贡献为

\max(0,a_u-s_u+c_u)-c_u

。

我们希望尽可能合并插头以减少操作次数，这与 2.2 中“尽量使用已有插头”的思想一致。

可以通过三个简单的讨论卡到

c_u

的上界：

显然 $c_u \le a_u$ 。
插头合并是两两配对，故 $c_u \le \left\lfloor \dfrac{s_u}{2} \right \rfloor$ 。
如果 $f_v$ 中存在一个很大的值，将其他插头都与此处的插头合并后，此处的插头仍然无法配对，因此 $c_u \le s_u - \max \limits_{v \in \operatorname{son}(u)} f_v$ 。

直接取交集是不对的。

仔细分析一下，设

S

为

u

节点未合并的插头数目。如果

u

已经是根节点，我们只希望最小化代价，那么代价

W

的一个上界为：将所有子树独立处理后加上

a_u

。下面的讨论中，我们将

W

取到这个上界再向下调整。

先做完所有插头合并操作，则 $f_u=\max(a_u,S)$ 。
一次插头合并中， $a_u \gets a_u-1$ ， $S \gets S-2$ ， $W \gets W-2$ 。
一次插头延伸中， $a_u \gets a_u-1$ ， $S$ 不变， $W \gets W-1$ 。

容易发现，存在一个时刻，使得在这个时刻之前，插头合并一定不劣于插头延伸，而之后插头延伸更优。具体地：

当 $S \le a_u$ 时，一次插头合并使得 $f_u \gets f_u-2$ ，一次插头合并等效于两次插头延伸，因此延伸更优;
当 $S > a_u$ 时， $f_u$ 至多减少 $1$ ，一次插头合并等效于一次插头延伸，而 $W$ 更小，故合并更优。

综上，得到

c_u

的第四个上界：

c_u \le s_u-a_u

。自底向上有递推式：

\begin{aligned} f_u&=a_u-c_u\\ c_u&=\max\left(0,\min\left( a_u, \left\lfloor \dfrac{s_u}{2} \right \rfloor, s_u - \max \limits_{v \in \operatorname{son}(u)} f_v, s_u-a_u \right)\right) \end{aligned}

进一步，当

u

不是根节点时，存在让

W

较大而增加

f_u

的策略。考虑调整法说明该策略不优：

当 $s_u \le a_u$ 时， $f_u \gets f_u+1$ 使得 $W \gets W+2$ ，显然劣于原策略。
当 $s_u > a_u$ 时，从 $c_u$ 的递推式可以看出 $c_u=0$ ，即不存在线头合并操作，自然也就无法调整了。

CPP

int f[N], s[N], c[N], ans;
void dfs(int u, int fa) {
	int mx = 0;
	for (int v : e[u]) {
		if (v == fa) continue;
		dfs(v, u), s[u] += f[v], mx = max(mx, f[v]);
	}
	c[u] = max(0LL, min({a[u], s[u] - a[u], s[u] / 2, s[u] - mx}));
	ans += max(0LL, a[u] - s[u] + c[u]) - c[u];
	f[u] = a[u] - c[u];
}

4.2 线性规划法

依旧解决对偶问题。

照搬 2.4 的做法，定义一个插头为延伸到当前位置的最大 $w_i$ 和，设

f_{0/1/2/3,u}

为已经完成

u

子树内的决策，

u

节点的决策是第

0/1/2/3

种情况时的最大得分。

容易写出四种情况的转移：

\begin{aligned} f_{0,u}&=-a_u+\sum _{v \in \operatorname{son}(u)} f_{0/1/2/3,v}\\ f_{1,u}&=\sum _{v \in \operatorname{son}(u)} f_{0/1,v}\\ f_{2,u}&=g(u)+\sum _{v \in \operatorname{son}(u)} f_{0/1,v}\\ f_{3,u}&=a_u+\sum _{v \in \operatorname{son}(u)} f_{0/1,v} \end{aligned}

这里

g(u)

的意思是，对于

f_{2,u}

，我们需要从

u

的儿子中选择一个，钦定其插头为

1

，其余儿子插头为

0

。可以按得分差值选择，即

g(u)=\max_{v \in \operatorname{son}(u)} f_{2/3,v}-f_{0/1,v}

CPP

int n, a[N], f[4][N];
void dfs(int u, int fa) {
    f[0][u] = -a[u], f[3][u] = a[u];
    int mx = 0;
    for (int v : e[u]) {
        if (v == fa) continue;
        dfs(v, u);
        f[0][u] += max({f[0][v], f[1][v], f[2][v], f[3][v]});
        f[1][u] += max(f[0][v], f[1][v]);
        f[2][u] += max(f[0][v], f[1][v]);
        mx = max(mx, max(f[2][v], f[3][v]) - max(f[0][v], f[1][v]));
        f[3][u] += max(f[0][v], f[1][v]);
    }
    f[2][u] += mx;
}

5. 基环树铲雪

给定一棵基环树，点权为 $a_i$ ，每次操作可将一条树链（或整个环）上的所有点权减 $1$ ，且操作过程中点权不能为负。

求使所有点权变为 $0$ 的最小操作次数。

5.1 线性规划法

解决对偶问题。

首先找出环，对环上挂的每棵树跑一遍 4.2 的 DP，结果记作

f_{0/1/2/3,u}

。

将环上的点从

1

开始重编号，然后仿照 3.3 进行环上 DP。先任找一个点断环为链，然后设

g_{0/1/2/3,u}

为第

u

个点的决策为

0/1/2/3

，已经完成

[1,u]

中决策后的最大得分。

转移如下：

\begin{aligned} g_{0,u}&=f_{0,u}+g_{0/1/2/3,u-1}\\ g_{1,u}&=f_{1,u}+g_{0/1,u-1}\\ g_{2,u}&=\max(f_{0/1,u}+g_{2/3,u-1},f_{2,u}+g_{0/1,u-1})\\ g_{3,u}&=f_{3,u}+g_{0/1,u-1} \end{aligned}

我们仍然可以使用 3.3 的做法，钦定终点插头为

0

，然后倒序再跑一次 DP。

同时，3.3 中的特判仍然需要，即环上有且仅有一个

w_i=1

。此时的选法类似 4.2 中的

g(u)

，选出唯一的点插头为

1

，其余插头为

0

，按得分差值选择。

使用拓扑排序找环，可以做到严格线性。

CPP

int n, a[N], deg[N], f[4][N], g[4][N];
bool on[N], tag[N];
vector<int> path, e[N];
void bfs() {
    fill(on + 1, on + n + 1, true);
    queue<int> q;
    for (int i = 1; i <= n; i++) {
        if (deg[i] == 1) q.emplace(i), on[i] = false;
    }
    while (!q.empty()) {
        int u = q.front(); q.pop();
        for (int v : e[u]) {
            if (--deg[v] == 1) q.emplace(v), on[v] = false;
        }
    }
    int s = find(on + 1, on + n + 1, true) - on, u = s;
    while (true) {
        path.emplace_back(u), tag[u] = true;
        bool flag = true;
        for (int v : e[u]) {
            if (on[v] && !tag[v]) u = v, flag = false;
        }
        if (flag) break;
    }
}

void dfs(int u, int fa) {
    f[0][u] = -a[u], f[3][u] = a[u];
    int mx = 0;
    for (int v : e[u]) {
        if (v == fa || on[v]) continue;
        dfs(v, u);
        f[0][u] += max({f[0][v], f[1][v], f[2][v], f[3][v]});
        f[1][u] += max(f[0][v], f[1][v]);
        f[2][u] += max(f[0][v], f[1][v]);
        mx = max(mx, max(f[2][v], f[3][v]) - max(f[0][v], f[1][v]));
        f[3][u] += max(f[0][v], f[1][v]);
    }
    f[2][u] += mx;
}

void _main() {
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i];
    for (int i = 1, u, v; i <= n; i++) {
        cin >> u >> v;
        e[u].emplace_back(v), e[v].emplace_back(u);
        deg[u]++, deg[v]++;
    }
    bfs();
    for (int i : path) dfs(i, -1);
    int m = path.size(), res = 0, mx = 0;
    for (int i : path) res += max(f[0][i], f[1][i]), mx = max(mx, max(f[2][i], f[3][i]) - max(f[0][i], f[1][i]));
    res += mx;
    auto work = [&]() -> void {
        for (int i = 1; i <= m; i++) {
            int u = path[i - 1];
            g[0][i] = f[0][u] + max({g[0][i - 1], g[1][i - 1], g[2][i - 1], g[3][i - 1]});
            g[1][i] = f[1][u] + max(g[0][i - 1], g[1][i - 1]);
            g[2][i] = max(
                max(f[0][u], f[1][u]) + max(g[2][i - 1], g[3][i - 1]),
                f[2][u] + max(g[0][i - 1], g[1][i - 1])
            );
            g[3][i] = f[3][u] + max(g[0][i - 1], g[1][i - 1]);
        }
        res = max({res, g[0][m], g[1][m]});
    };
    work(), reverse(path.begin(), path.end()), work();
    cout << res;
}

6. 练习

6.1 单点清空铲雪

大手子 zzh 提出的问题。

给定序列 $a_i$ ，每次操作可将一个区间内的所有元素减 $1$ ，或将某个点的值直接置 $0$ 。

操作过程中值不能为负，求使所有元素变为 $0$ 的最小操作次数。

题解

考虑 2.3 的笛卡尔树法。

一个重要观察是：对于一个区间，要么直接推平（全部置

0

），要么先减去区间最小值再从最小值处分裂。因为减到一半再使用单点置

0

必然不如直接推平优。

基于此，可以魔改一下 2.3 的式子，设

f(l,r,v)

为区间

[l,r]

已经减去了

v

后的答案，找到区间最小值

a_x

，则：

f(l,r,v)=\min\left(r-l+1,f(l,x-1,v+a_x)+a_x-v+f(x+1,r,v+a_x)\right)

第一条转移对应推平，第二条转移对应减去最小值。

仍然可以小根笛卡尔树上 DP 做到

O(n)

。

CPP

int n, a[N], rt, l[N], r[N], sz[N], f[N];
void build() {
    stack<int> st;
    for (int i = 1; i <= n; i++) {
        while (!st.empty() && a[st.top()] > a[i]) l[i] = st.top(), st.pop();
        if (!st.empty()) r[st.top()] = i;
        else rt = i;
        st.emplace(i);
    }
}

void dfs(int u, int h) {
    if (!u) return;
    dfs(l[u], a[u]), dfs(r[u], a[u]);
    sz[u] = sz[l[u]] + sz[r[u]] + 1;
    f[u] = min(sz[u], a[u] - h + f[l[u]] + f[r[u]]);
}

void _main() {
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i];
    build(), dfs(rt, 0);
    cout << f[rt];
}

6.2 CF1954E

CF1954E Chain Reaction。

给出一个序列 $a_i$ ，对 $k=1,2,3,\cdots,\max \limits_{i=1}^n a_i$ 解决以下问题：

每次操作将一个区间内的所有元素减 $k$ ，操作时元素值须为正。求使所有元素变为非正的最小操作次数。

$n,V \le 10^5$ 。3 秒，512 MB。

题解

注意到

k=1

时问题等价于序列铲雪。

对于一般的

k

，一个数字

a_i

需要

\left \lceil \dfrac{a_i}{k} \right \rceil

次操作才能变为非正。考虑 2.1 的差分法，设

d_i=\left \lceil \dfrac{a_i}{k} \right \rceil-\left \lceil \dfrac{a_{i-1}}{k} \right \rceil

，然后基于类似的讨论就能得到答案是

f(k)=\sum_{i=1}^n \max(0,d_i)

将贡献拆到每个

a_i > a_{i-1}

的位置上。其对于

f(k)

的贡献值为

\left \lceil \dfrac{a_i}{k} \right \rceil

和

-\left \lceil \dfrac{a_{i-1}}{k} \right \rceil

。

注意到式子中出现了除

k

取整的形式，考虑上取整数论分块。先枚举位置，再做一遍数论分块，贡献为一个区间加的形式，差分一下，复杂度

O(n \sqrt{V})

。

CPP

int n, m, a[N], d[N];

void _main() {
	cin >> n;
	for (int i = 1; i <= n; i++) cin >> a[i], m = max(m, a[i]);
	for (int i = 1; i <= n; i++) {
		for (int l = 1, r; l <= m; l = r + 1) {
			int v = (a[i] + l - 1) / l;
			r = min(m, v == 1 ? INT_MAX : (a[i] - 1) / (v - 1));
			if (a[i] > a[i - 1]) d[l] += v, d[r + 1] -= v;
			if (a[i] < a[i + 1]) d[l] -= v, d[r + 1] += v;
		}
	}
	for (int i = 1; i <= m; i++) d[i] += d[i - 1], cout << d[i] << ' ';
}

6.3 环上铲雪·构造

P14682 [ICPC 2025 Yokohama R] Seagull Population。

给定环 $a_i$ ，每次操作可将一个区间（或整个环）上的所有元素减 $1$ ，且操作过程中元素值不能为负。

求使所有元素变为 $0$ 的最小操作次数，并且构造方案。

$n,V \le 2 \times 10^5$ 。2 秒，2048 MB。

题解

考虑根据 3.1 的充分性证明来构造。

由于我比较魔怔，自然想到用线段树来维护环上的最大值结构。

对于 $M<D$ ：
- 我们需要找到一个全为最大值的极长区间，故线段树需要维护最大值、最大值的出现位置。
- 同时还需要记录最小值，这样我们可以从最左位置出发跑线段树二分，找到极长区间的右端点。
- 注意处理跨过 $1$ 号点的情况，做一个反方向的线段树二分即可。
对于 $M=D$ ：
- 我们还需记录这个“最小的包含了所有最大值的区间”，称这个结构为一个 Gap。
- 需记录 Gap 最长长度及左右端点。
- 在讨论 Gap 的形态时，需要区分 Gap 是否跨过 $1$ 号点。

综上，我们用线段树维护七个值：最大值、最小值、最大值的最左 / 最右出现位置、Gap 最长长度、Gap 左右端点。这些信息都具有可加性。最终复杂度为

O(n \log n)

。

CPP

int n, a[N];

struct node {
    int mx, mn, lm, rm, gap, lg, rg;
};
node operator+ (const node& a, const node& b) {
    if (a.mx > b.mx) return node{a.mx, min(a.mn, b.mn), a.lm, a.rm, a.gap, a.lg, a.rg};
    if (a.mx < b.mx) return node{b.mx, min(a.mn, b.mn), b.lm, b.rm, b.gap, b.lg, b.rg};
    node res{a.mx, min(a.mn, b.mn), a.lm, b.rm, -1, -1, -1};
    int d = b.lm - a.rm; 
    if (a.gap >= max(b.gap, d)) res.gap = a.gap, res.lg = a.lg, res.rg = a.rg;
    else if (b.gap >= max(a.gap, d)) res.gap = b.gap, res.lg = b.lg, res.rg = b.rg;
    else res.gap = d, res.lg = a.rm, res.rg = b.lm;
    return res;
}
struct segtree {
#define ls (rt << 1)
#define rs (rt << 1 | 1)
    node val[N << 2]; int tag[N << 2];
    void pushup(int rt) {val[rt] = val[ls] + val[rs];}
    void apply(int rt, int c) {val[rt].mx += c, val[rt].mn += c, tag[rt] += c;} 
    void pushdown(int rt) {
        if (!tag[rt]) return;
        apply(ls, tag[rt]), apply(rs, tag[rt]), tag[rt] = 0;
    }
    void build(int l = 1, int r = n, int rt = 1) {
        if (l == r) return val[rt] = node{a[l], a[l], l, l, 0, -1, -1}, void();
        int mid = (l + r) >> 1;
        build(l, mid, ls), build(mid + 1, r, rs), pushup(rt);
    }
    void change(int tl, int tr, int c, int l = 1, int r = n, int rt = 1) {
        if (tl <= l && r <= tr) return apply(rt, c), void();
        pushdown(rt);
        int mid = (l + r) >> 1;
        if (tl <= mid) change(tl, tr, c, l, mid, ls);
        if (tr > mid) change(tl, tr, c, mid + 1, r, rs);
        pushup(rt);
    }
    int qval(int x, int l = 1, int r = n, int rt = 1) {
        if (l == r) return val[rt].mx;
        pushdown(rt);
        int mid = (l + r) >> 1;
        return x <= mid ? qval(x, l, mid, ls) : qval(x, mid + 1, r, rs);
    }
    int qleft(int tl, int tr, int c, int l = 1, int r = n, int rt = 1) {
        if (val[rt].mn >= c) return -1;
        if (l == r) return l;
        pushdown(rt);
        int mid = (l + r) >> 1, res = -1;
        if (tl <= mid) res = qleft(tl, tr, c, l, mid, ls);
        if (res != -1) return res;
        return tr > mid ? qleft(tl, tr, c, mid + 1, r, rs) : -1;
    }
    int qright(int tl, int tr, int c, int l = 1, int r = n, int rt = 1) {
        if (val[rt].mn >= c) return -1;
        if (l == r) return l;
        pushdown(rt);
        int mid = (l + r) >> 1, res = -1;
        if (tr > mid) res = qright(tl, tr, c, mid + 1, r, rs);
        if (res != -1) return res;
        return tl <= mid ? qright(tl, tr, c, l, mid, ls) : -1;
    }
    node all() {return val[1];}
} sgt;

void A(int l, int r) {
    cout << l << ' ' << r << '\n';
	if (l <= r) sgt.change(l, r, -1);
	else sgt.change(l, n, -1), sgt.change(1, r, -1);
}

void _main() {
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i];
    int M = *max_element(a + 1, a + n + 1), D = abs(a[1] - a[n]);
    for (int i = 2; i <= n; i++) D += abs(a[i] - a[i - 1]);
    D /= 2, cout << max(M, D) << '\n';
    if (max(M, D) > 2e5) return;
    sgt.build();
    while (M > D) A(1, n), M--;
    while (D > M) {
        int l = sgt.all().lm, ed = sgt.qleft(l, n, M), r = ed == -1 ? n : ed - 1;
        if (l == 1 && sgt.qval(n) == M) A(sgt.qright(1, n, M) + 1, r);
        else A(l, r);
        D--, M = sgt.all().mx;
    }
    while (D--) {
        int igap = sgt.all().gap, ogap = n - sgt.all().rm + sgt.all().lm;
        if (ogap >= igap) A(sgt.all().lm, sgt.all().rm);
        else A(sgt.all().rg, sgt.all().lg);
    }
}

6.4 AGC010C

AT_agc010_c [AGC010C] Cleaning。

给出一棵树，每个点有一个点权 $a_i$ ，一次操作将一条起终点均为叶子的树链上的所有元素减去 $1$ 。

要求操作过程中点权始终非负。判断是否可以使得所有元素全变为 $0$ 。

$n \le 10^5$ ，2 秒，256 MB。

题解

考虑 4.1 的插头法。

特判

n=2

以后，任选一个度数不为

1

的点为根，然后定义一个插头为一条可以向父亲 / 兄弟延伸的操作。

仿照 4.1，设

f_u

为

u

节点向上延伸的插头数目，记

s_u = \sum \limits_{v \in \operatorname{son(u)}} f_v

，则

u

处插头合并次数为

\dfrac{s_u-f_u}{2}

，可列方程为

a_u=f_u+\dfrac{s_u-f_u}{2}

解得

f_u=2a_u-s_u

。特别地，对叶子有

f_u=a_u

。

考察可行性的充要条件。对

u

点有：

$0 \le f_u \le a_u$ 。
$\max \limits_{v \in \operatorname{son}(u)} f_v \le a_u$ 。对应 4.1 的其中一个讨论。

自底向上递推得到所有

f_u,s_u

，按条件判定即可。

CPP

int n, a[N], d[N];
long long f[N], s[N];
bool dfs(int u, int fa) {
	if (d[u] == 1) return f[u] = a[u], true;
	long long mx = 0;
	for (int v : e[u]) {
		if (v == fa) continue;
		if (!dfs(v, u)) return false;
		s[u] += f[v], mx = max(mx, f[v]);
	} 
	f[u] = 2 * a[u] - s[u];
	return 0 <= f[u] && f[u] <= a[u] && mx <= a[u];
}

void _main() {
	cin >> n;
	for (int i = 1; i <= n; i++) cin >> a[i];
	if (n == 2) return cout << (a[1] == a[2] ? "YES" : "NO"), void();
	for (int i = 1, u, v; i < n; i++) cin >> u >> v, e[u].emplace_back(v), e[v].emplace_back(u), d[u]++, d[v]++;
	int rt = 1;
	for (int i = 1; i <= n; i++) if (d[i] > 1) rt = i; 
	cout << (dfs(rt, -1) && f[rt] == 0 ? "YES" : "NO");
}

6.5 跳跃铲雪

P6631 [ZJOI2020] 序列。

给定序列 $a_i$ ，每次操作可将一个区间内的所有元素减 $1$ ，或将一个区间内奇数位置 / 偶数位置的元素减 $1$ 。

操作过程中值不能为负，求使所有元素变为 $0$ 的最小操作次数。

$n \le 10^5$ ，多测 $T \le 10$ ，1 秒，512 MB。

题解

考虑 2.2 的插头法。

称第一类操作为“直线”，二三类操作为“跳线”，则可以类似定义“直插头”和“跳插头”。

我们声称，一段从

1

开始的长度

\ge 2

的非

0

极长区间用直线覆盖不劣。

事实上，设区间

[l,r]

满足

\forall i \in [l, r], a_i > 0

，且

a_{l-1}=a_{r+1}=0

，则

[l,r]

为操作的极长区间。考虑调整，显然不可向

r+1

连出插头，合法方案只可能由

r-1

开始延伸跳插头。则此时代价至少为

2

。而原方案的代价恰好为

2

，故调整不优。

于是可以按

a_i,a_i+1

分类讨论：

若 $a_i>0,a_{i+1}>0$ ，从 $i$ 开始延伸一个直插头。
若 $a_i>0,a_{i+1}=0$ ，从 $i$ 开始延伸一个跳插头。
若 $a_i=0$ ，延迟决策。

设

A,B

表示当前位置的直插头和跳插头数目。若

a_i \ge A+B

，则

a_i \gets a_i-A-B

。否则有

W=A+B-a_i

个插头无法延伸。

记录下

W

并延迟决策，则考虑新位置

a_j

，该位置有

W

条无代价的插头。在讨论对答案的贡献时处理一下，一遍扫描即可出答案。

CPP

const int N = 1e5 + 5;
int n, a[N];   

void _main() {
	cin >> n;
	for (int i = 1; i <= n; i++) cin >> a[i];
	int res = 0, A = 0, B = 0, nB = 0, W = 0;           // nB 维护不同奇偶性的跳插头数目
	for (int i = 2; i <= n + 1; swap(B, nB), i++) {
		if (a[i] < A + B) {
			W = A + B - a[i];
			if (W > B) A -= W - B, W -= W - B;
			if (W > A) B -= W - A, W -= W - A;
			A -= W, B -= W, a[i] -= W;
		} 
		a[i] -= A + B;
		int C = min(a[i - 1], a[i]);                    // 新增直插头数目
		res += C, a[i - 1] -= C, a[i] -= C, A += C;     // 直插头
		res += a[i - 1], nB += a[i - 1], a[i - 1] = 0;  // 跳插头
		if (W) a[i] += W, res -= W, W = 0;              // 标记
	} cout << res << '\n';
}

另解

考虑 2.4 的线性规划法。

解决对偶问题：找到一组整数

w_i

，对所有区间 / 下标为奇数 / 偶数的连续段

w_i

之和不大于

1

，最大化

a_iw_i

的和。

不难证明

w_i \in \{-1,0,1\}

，容易设计出 DP 状态：

f_{a,b,c,i}

表示已完成

[1,i]

中的决策，在第

i

个位置，三种插头分别为

a,b,c

的最大得分。注意到

a,b,c \in \{0,1\}

。刷表转移即可。

CPP

int n, A[N], f[2][2][2][N];
void _main() {
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> A[i];
    memset(f, 0xcf, sizeof(f));
    f[0][0][0][0] = 0;
    for (int i = 1; i <= n; i++) {
        for (int a : {0, 1}) for (int b : {0, 1}) for (int c : {0, 1}) {
            for (int w : {-1, 0, 1}) {
                int na = max(0LL, a + w), nb = max(0LL, b + (i % 2 ? w : 0)), nc = max(0LL, c + (i % 2 ? 0 : w));
                if (na <= 1 && nb <= 1 && nc <= 1) f[na][nb][nc][i] = max(f[na][nb][nc][i], f[a][b][c][i - 1] + w * A[i]);
            }
        }
    }
    int res = 0;
    for (int a : {0, 1}) for (int b : {0, 1}) for (int c : {0, 1}) res = max(res, f[a][b][c][n]);
    cout << res << '\n';
}

6.6 限长铲雪

P8182 「EZEC-11」雪的魔法。

给定长度为 $n$ 的序列 $a$ ，有 $q$ 次询问。

一次操作可选择一个长度不超过 $k$ 的子区间，将其中所有数减一。

求将区间 $[l,r]$ 内所有数变为 $0$ 的最小操作次数。

$k, n, q \le 10^5$ ，1.2 秒，512 MB。

题解

前置知识。

考虑 2.4 的线性规划法，解决对偶问题。将区间中每个位置赋一个权值

w_i \in \{-1,0,1\}

，满足任意长度不超过

k

的子区间的权值和不超过

1

。最大化

\sum a_i w_i

。

考虑

k \ge n

的情况，此时原问题等价于序列铲雪。注意到 2.1 给出的式子

\sum \limits_{i=1}^n \max(0,d_i)

，我们称：这种答案是平凡的。对于对偶问题，这样的答案会偏小，因为对偶问题的限制是相对松的。

设

f_i

为考虑到第

i

个位置的答案，初始

f_l=a_l

。对于

i=l+1,l+2,\cdots,r

，有如下转移方程：

f_i=\max(f_{i-1}+\max(0,a_i-a_{i-1}),f_{i-k}+a_i)

其中，

f_{i-1}+\max(0,a_i-a_{i-1})

是平凡的。而

f_{i-k}+a_i

的意思是将

[i-k+1,i-1]

中的权值全部置

0

，并且令

w_i=1

。

这个 DP 的正确性不是很显然。但是仔细思考一下，对于一个不平凡的情况，如果

[i-k+1,i-1]

中存在非零权值，那么这总能规约到一个平凡情况。因此，我们得到了一个

O(nq)

做法。

观察一下这个 DP 式子，使用前置知识中的网格图分治优化 DP 即可。与网格图分治不同的点在于起点

l

带了点权，更新最短路时注意带上。复杂度

O((n+q) \sqrt{n})

。

CPP

const int N = 2e5 + 5;
const int64 inf = 1e18;

int n, k, q;
int64 a[N], ans[N], dis[N];
using query = tuple<int, int, int, int, int>;  // {x1, y1, x2, y2, id}
vector<query> qry;

void update(int lx, int rx, int ly, int ry, int sx, int sy, const vector<query>& q) {
    int s = sx * k + sy;
    for (int x = lx; x <= rx; x++) {
        for (int y = ly; y <= ry; y++) dis[x * k + y] = -inf;
    }
    dis[s] = 0;
    auto chk = [&](int i) -> bool {return lx <= i / k && i / k <= rx && ly <= i % k && i % k <= ry;};
    for (int x = sx; x >= lx; x--) {
        for (int y = ry; y >= ly; y--) {
            int i = x * k + y;
            if (i > s) continue;
            if (chk(i + 1)) dis[i] = max(dis[i], dis[i + 1] + max(0LL, a[i + 1] - a[i]));
            if (chk(i + k)) dis[i] = max(dis[i], dis[i + k] + a[i + k]);
        }
    }
    for (int x = sx; x <= rx; x++) {
        for (int y = ly; y <= ry; y++) {
            int i = x * k + y;
            if (i < s) continue;
            if (chk(i + 1)) dis[i + 1] = max(dis[i + 1], dis[i] + max(0LL, a[i + 1] - a[i]));
            if (chk(i + k)) dis[i + k] = max(dis[i + k], dis[i] + a[i + k]);
        }
    }
    for (const auto& [x1, y1, x2, y2, id] : q) {
        if (x1 * k + y1 > s || x2 * k + y2 < s) continue;
        ans[id] = max(ans[id], a[x1 * k + y1] + dis[x1 * k + y1] + dis[x2 * k + y2]);
    }
}

void solve(int lx, int rx, int ly, int ry, vector<query> q) {
    if (lx > rx || ly > ry || q.empty()) return;
    if (rx - lx > ry - ly) {
        int mid = (lx + rx) >> 1;
        for (int y = ly; y <= ry; y++) update(lx, rx, ly, ry, mid, y, q);
        vector<query> ql, qr;
        for (const auto& [x1, y1, x2, y2, id] : q) {
            if (x1 < mid && x2 < mid) ql.emplace_back(x1, y1, x2, y2, id);
            if (mid < x1 && mid < x2) qr.emplace_back(x1, y1, x2, y2, id);
        }
        solve(lx, mid - 1, ly, ry, ql), solve(mid + 1, rx, ly, ry, qr);
    } else {
        int mid = (ly + ry) >> 1;
        if (ly == 0 && ry == k - 1) {  // 斜边
            for (int x = lx; x <= rx; x++) update(lx, rx, ly, ry, x, 0, q);
        }
        for (int x = lx; x <= rx; x++) update(lx, rx, ly, ry, x, mid, q);
        vector<query> ql, qr;
        for (const auto& [x1, y1, x2, y2, id] : q) {
            if (y1 < mid && y2 < mid) ql.emplace_back(x1, y1, x2, y2, id);
            if (mid < y1 && mid < y2) qr.emplace_back(x1, y1, x2, y2, id);
        }
        solve(lx, rx, ly, mid - 1, ql), solve(lx, rx, mid + 1, ry, qr);
    }
}

void _main() {
    cin >> n >> k >> q;
    for (int i = 1; i <= n; i++) cin >> a[i];
    for (int i = 1, l, r; i <= q; i++) {
        cin >> l >> r;
		qry.emplace_back(l / k, l % k, r / k, r % k, i);
    }
    solve(0, n / k, 0, k - 1, qry);
    for (int i = 1; i <= q; i++) cout << ans[i] << '\n';
}

6.7 二元铲雪

P3543 [POI 2012] WYR-Leveling Ground。

给出一个序列 $h_i$ ，一次操作将一个区间上的所有元素加上或减去 $a$ ，或者加上或减去 $b$ 。

要求操作过程中点权始终非负。求使得所有元素全变为 $0$ 的最小操作数，或者报告无解。

$n \le 10^5$ ，1 秒，125 MB。

题解

考虑每个数字一定是

ax+by

的形式，由裴蜀定理先判掉无解。有解则将

a,b,h_i

都除掉

\gcd(a,b)

，显然不会影响答案。

考虑 2.1 的差分法，令

d_i=h_i-h_{i-1}

，特别地

d_{n+1}=-h_n

。则题目转化为：

选择 $i,j$ ，令 $d_i \gets d_i+a, d_j \gets d_j -a$ 。
选择 $i,j$ ，令 $d_i \gets d_i+b,d_j \gets d_j-b$ 。
目标为 $\forall 1 \le i \le n+1, d_i=0$ 。

下文令

n \gets n +1

。

对于

d_i

，设我们在该位置进行了

x_i

次

+a

，

y_i

次

+b

，负数次操作的意义则为区间减。可以列出方程：

ax_i+by_i=-d_i

容易用 exGCD 求得

ax+by=\gcd(a,b)

的一组特解

x_0,y_0

，进而得到通解形式：

x_i=x_0+k \times \dfrac{b}{d_i}

y_i=y_0-k \times \dfrac{a}{d_i}

2.1 的结论告诉我们，全局操作次数为

\dfrac{1}{2} \sum_{i=1}^n \left( |x_i|+|y_i| \right)

现在我们重新表述题目：

找到一组 $x_i,y_i$ $x_{i}, y_{i}$ 满足：
- $x_i=x_0+k \times \dfrac{b}{d_i}$ 。
- $y_i=y_0-k \times \dfrac{a}{d_i}$
- $\sum \limits_{i=1}^n x_i=0$ 。这等价于 $\sum \limits_{i=1}^n y_i=0$ 。
在此基础上，最小化 $\dfrac{1}{2} \sum \limits_{i=1}^n \left( |x_i|+|y_i| \right)$ 。

注意到代价变化量

F(i)=|x_0+ib|-|y_0-ia|

是一个分段线性函数，左端单调减，右端单调增，中间段单调减或者单调增。

下图展示了

x_0=-3,y_0=3,a=2,b=-1

时的情形。

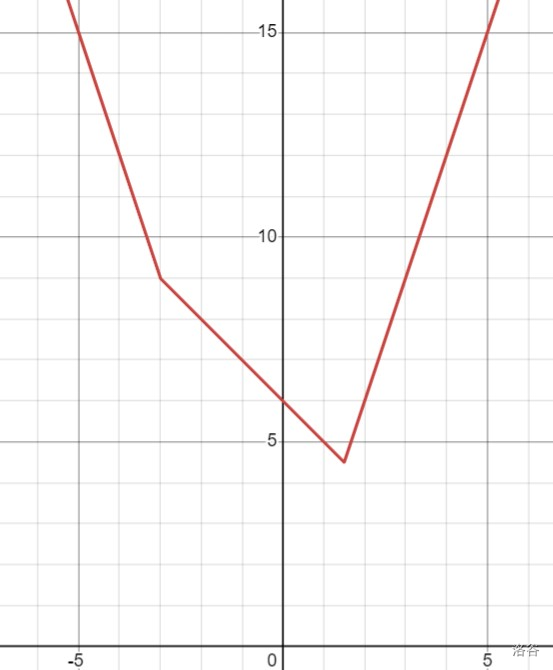
忽略第三条限制，把

x_i,y_i

取到谷点，这样代价自然最小。注意到代价关于调整距离的函数应当具有凸性，可以用神奇调整法使得

\sum \limits_{i=1}^n x_i=0

。

设当前位置为

p_i

。每次对

p_i

做一次调整，

x_i

都会移动

b

个单位。故总调整次数为

\dfrac{1}{b}\left| \sum \limits_{i=1}^n x_i \right|

。

因为斜率分

O(1)

段，我们可以用一个 vector 存下每种决策。具体地，记录二元组

(w_i,s_i)

表示以代价

w_i

移动

s_i

步。按

w_i

排序，顺次取就是正确的。

压力给到如何求

(w_i,s_i)

。设

D(i)=F(i \pm 1)-F(i)

，其中

\pm

的符号取决于调整的方向。

以向右调整为例，可以求出两个拐点

\left\lfloor -\dfrac{x_i}{b} \right\rfloor,\left\lfloor \dfrac{y_i}{a}\right\rfloor

。顺次遍历每个分界点，对分界点中间的段计算。

本题有一个神奇的性质：每轮调整只需调整一次。证明。

代码细节上，注意若干处需要 __int128。

CPP

const int N = 1e5 + 5;

int n, a, b, g, h[N], d[N];
void exgcd(int128 a, int128 b, int128& x, int128& y) 
{b ? (exgcd(b, a % b, y, x), y -= a / b * x) : (x = 1, y = 0);}
tuple<int128, int128, int128> info[N];
int128 _abs(int128 x) {return x >= 0 ? x : -x;}  

void _main() {
	cin >> n >> a >> b, g = gcd(a, b);
    for (int i = 1; i <= n; i++) {
        cin >> h[i];
        if (h[i] % g) return cout << -1, void(); 
        h[i] /= g;
    }
    for (int i = 1; i <= n + 1; i++) d[i] = h[i] - h[i - 1];
    n++, a /= g, b /= g;
    if (a < b) swap(a, b);
    int128 x0, y0; exgcd(a, b, x0, y0);
	
	int128 cost = 0, cur = 0;
	auto work1 = [&]() -> void {
		for (int i = 1; i <= n; i++) {
			// x * a + y * b = -d[i]
			int128 v = -d[i], x = (x0 * v % b + b) % b, y = (v - a * x) / b;
			auto F = [&](int i) -> int128 {return _abs(x + i * b) + _abs(y - i * a);};
			int128 p = y / a;
			if (F(y / a - 1) < F(p)) p = y / a - 1;
			if (F(y / a + 1) < F(p)) p = y / a + 1;
			cost += F(p), cur += x + p * b;
			info[i] = {x, y, p};
		}
	};
	work1();
	int offset = -(cur / b), dir = offset < 0 ? -1 : 1;
	if (offset == 0) return cout << static_cast<u64>(cost / 2), void();
	
	vector<pair<int128, int128>> vec;
	auto work2 = [&]() -> void {
		for (int i = 1; i <= n; i++) {
			auto [x, y, p] = info[i];
			auto F = [&](int i) -> int128 {return _abs(x + i * b) + _abs(y - i * a);};
			auto D = [&](int i) -> int128 {return F(i + dir) - F(i);};
			int p1 = floor(-1.0 * x / b), p2 = floor(1.0 * y / a);
			if (dir == 1) {
				int cur = p;
				vector<int> tmp = {p1, p2};
				sort(tmp.begin(), tmp.end());
				for (int pos : tmp) {
					if (pos < cur) continue;
					if (pos > cur) vec.emplace_back(D(cur), pos - cur);  // ->
					vec.emplace_back(D(p), 1), cur = pos + 1;   // 跨过 p -> p+1
				}
				vec.emplace_back(D(cur), _abs(offset));  // 整体
			} else {
				int cur = p;
				vector<int> tmp = {p1 + 1, p2 + 1};
				sort(tmp.begin(), tmp.end(), greater<int>());
				for (int pos : tmp) {
					if (pos > cur) continue;
					if (pos < cur) vec.emplace_back(D(cur), cur - pos);  // <-
					vec.emplace_back(D(p), 1), cur = pos - 1;   // 跨过 p-1 <- p
				}
				vec.emplace_back(D(cur), _abs(offset));  // 整体
			}
		}
	};
	work2();
	
	sort(vec.begin(), vec.end());
	int128 res = cost, need = _abs(offset);
	for (auto [val, cnt] : vec) {
		int128 w = min(cnt, need);
		res += w * val, need -= w;
		if (need <= 0) break;
	} cout << static_cast<u64>(res / 2);
}

也可以使用优先队列来维护调整法的过程。

6.8 循环铲雪

P4846 LJJ爱数书。

给定长度为 $n$ 的序列 $a$ ，有 $q$ 次询问。

一次询问给出 $l,r,m$ ，求解如下问题：每次操作将一个区间内的所有元素 $\pm 1$ 对 $m$ 取模，求使所有元素变为 $0$ 的最小操作次数。

$n \le 2 \times 10^5$ ， $q \le 10^5$ ，5 秒，250 MB。

题解

考虑 2.1 的差分法。

设

d_i=a_i-a_{i-1}

，特别地

d_l=a_l,d_{r+1}=-a_r

，于是：

原操作等价于：选择两个下标 $l \le i < j \le r$ ，令 $d_i \gets d_i \pm 1$ ， $d_j \gets d_j \mp 1$ 。
目标状态为 $\forall l \le i \le r+1, d_i \equiv 0 \pmod m$ 。

注意到如果

|d_i| \ge 2m

，直接调整不如先模

m

再处理，因此最优时

d_i

只会落在

\{-m, 0, m\}

中，且

-m

与

m

必须成对出现。

如果忽略取模的限制，根据 2.1 结论，最小操作次数为

\dfrac{1}{2} \sum \limits_{i=l}^{r+1} |d_i|

，即每个

d_i

贡献

|d_i|

。

现在考虑模

m

的影响，相当于我们可以预先将某些

d_i

加上或减去

m

：

若 $d_i < 0$ ，可预先加上 $m$ ，此时对答案的额外贡献为 $m + 2d_i$ 。
若 $d_i > 0$ ，可预先减去 $m$ ，此时对答案的额外贡献为 $m - 2d_i$ 。

记这两种决策分别为

X

和

Y

。由于

-m

和

m

必须成对出现，因此

X

和

Y

的数量也必须相等。将所有

X

决策的贡献值

x_i

和

Y

决策的贡献值

y_i

分别升序排序，并取其前缀和，则总答案为：

\dfrac{1}{2} \left(\sum _{i=l}^r |d_i|+\min_{k} \left(\sum_{i=0}^k x_i+\sum_{i=0}^k y_i\right)\right)

因此我们得到一个

O(nq \log n)

的做法：

CPP

int solve(int l, int r, int m) {
	vector<int> x, y;
	int sum = 0;
	for (int i = l; i <= r + 1; i++) {
		int d = a[i] - a[i - 1];
		if (i == l) d = a[l];
		if (i == r + 1) d = -a[r];
		if (d < 0) x.emplace_back(m + 2 * d);
		else y.emplace_back(m - 2 * d);
		sum += abs(d);
	}
	sort(x.begin(), x.end()), sort(y.begin(), y.end());
	int xn = x.size(), yn = y.size();
	for (int i = 1; i < xn; i++) x[i] += x[i - 1];
	for (int i = 1; i < yn; i++) y[i] += y[i - 1];
	int res = sum;
	for (int i = 0; i < min(xn, yn); i++) res = min(res, sum + x[i] + y[i]);
	return res / 2;
}

对着这段代码优化。

记

f(k)=\sum \limits_{i=0}^k x_i+\sum \limits_{i=0}^k y_i

，将

f(k)

打表出来可以发现

f(k)

是单谷的，下面证明这一发现。

将所有正差分 $d_i$ 记为 $p$ ，所有负差分 $d_i$ 记为 $q$ 。
$\begin{aligned} f(k)&=\sum \limits_{i=0}^k x_i+\sum \limits_{i=0}^k y_i\\ &=\sum \limits_{i=0}^k \left(2m+2(p_i-q_i)\right)\\ &=2mk+2\sum_{i=0}^k (p_i-q_i)\\ \Delta f(k) &=2m+2(p_{k+1}-q_{k+1}) \end{aligned}$
由 $p_i$ 单调不降， $q_i$ 单调不升， $p_i-q_i$ 单调不降。则 $\Delta f(k)$ 单调不降，即 $f(k)$ 有凸性。

得到这个结论以后，我们可以直接三分出谷点。瓶颈仅在于求

x,y

。

注意到

x_i

和

y_i

可由

d_i

直接计算，且

d_i

随下标连续变化，我们可以用两棵可持久化权值线段树来维护所有

x_i,y_i

的值，并支持查询前

k

小的

x_i,y_i

之和。

具体实现时，

d_l

和

d_{r+1}

需要单独处理，可以在线段树二分时带一个参数。为了方便编写，代码中的数字取了相反数。

复杂度

O(q \log n \log V)

。实现细节上，应当注意特判

l=r

和一些边界的处理。

CPP

const int N = 2e5 + 5, M = 1 << 30;
int n, q, l, r, m, a[N], cx[N], cy[N], pre[N];

struct segtree {
#define ls lson[rt]
#define rs rson[rt]
	int tot, root[N], lson[N << 5], rson[N << 5], cnt[N << 5], sum[N << 5];
	void pushup(int rt) {cnt[rt] = cnt[ls] + cnt[rs], sum[rt] = sum[ls] + sum[rs];}
	int clone(int rt) {
		int u = ++tot;
		lson[u] = ls, rson[u] = rs, cnt[u] = cnt[rt], sum[u] = sum[rt];
		return u;
	}
	int insert(int x, int l, int r, int rt) {
		int p = clone(rt);
		if (l == r) return cnt[p]++, sum[p] += l, p;
		int mid = (l + r) >> 1;
		if (x <= mid) lson[p] = insert(x, l, mid, ls);
		else rson[p] = insert(x, mid + 1, r, rs);
		return pushup(p), p;
	}
	int ask(int k, int x, int l, int r, int u, int v) {
		if (k == 0) return 0;
		if (l == r) return k * l;
		int mid = (l + r) >> 1, num = cnt[rson[u]] - cnt[rson[v]] + (mid < x && x <= r);
		if (num >= k) return ask(k, x, mid + 1, r, rson[u], rson[v]);
		int val = sum[rson[u]] - sum[rson[v]] + (mid < x && x <= r ? x : 0);
		return ask(k - num, x, l, mid, lson[u], lson[v]) + val;
	}
	segtree() : tot(0) {root[0] = 0, lson[0] = rson[0] = cnt[0] = sum[0] = 0;}
	int ask(int l, int r, int k, int x) {return ask(k, x, 0, M, root[r], root[l - 1]);}
	void push(int x) {root[x] = root[x - 1];}
	void push(int x, int v) {root[x] = insert(v, 0, M, root[x - 1]);}
} X, Y;

void _main() {
	cin >> n >> q;
	for (int i = 1; i <= n; i++) cin >> a[i];
	for (int i = 1; i <= n + 1; i++) {
		int d = a[i] - a[i - 1];
		pre[i] = pre[i - 1] + abs(d), cx[i] = cx[i - 1], cy[i] = cy[i - 1];
		if (d < 0) X.push(i, -d), Y.push(i), cx[i]++;
		else X.push(i), Y.push(i, d), cy[i]++;
	}
	while (q--) {
		cin >> l >> r >> m;
		if (l == r) {cout << min(a[l], m - a[l]) << '\n'; continue;}
		int sum = pre[r] - pre[l] + a[l] + a[r];
		auto f = [&](int k) -> int {return sum / 2 + m * k - X.ask(l + 1, r, k, a[r]) - Y.ask(l + 1, r, k, a[l]);};
		auto sol = [&](int l, int r) -> int {
			int p = 0;
			while (l <= r) {
				int m1 = l + (r - l) / 3, m2 = r - (r - l) / 3;
				if (f(m1) < f(m2)) r = m2 - 1, p = m1;
				else l = m1 + 1, p = m2;
			} return p;
		};
		int p = sol(0, min(cx[r] - cx[l], cy[r] - cy[l]) + 1);
		cout << min(sum / 2, f(p)) << '\n';
	}
}

6.9 循环铲雪·改

给出 $q$ 次操作，每次操作对 $a$ 中不小于 $u$ 的数加上 $v$ ，然后查询以 $m+v$ 为模数的链上循环铲雪。操作之间独立。

$1 \le n, q \le 2\times 10^5$ ，3 秒，512 MB。

题解

在 6.8 中，我们注意到

f(k)

是单谷函数，因此可以三分答案，这在本题中仍然适用。需要考虑如何动态维护

x,y

。

对于一次询问

(u, v)

，考虑差分

d_i = a_i - a_{i-1}

的变化情况：

若 $a_i \ge u, a_{i-1} \ge u$ ， $d_i$ 不变。
若 $a_i < u, a_{i-1} < u$ ， $d_i$ 不变。
若 $a_i \ge u, a_{i-1} < u$ ，此时原 $d_i>0$ 且 $d_i \gets d_i+v$ 。
若 $a_i < u, a_{i-1} \ge u$ ，此时原 $d_i < 0$ 且 $d_i \gets d_i-v$ 。

综上，当

u \in \left(\min(a_i, a_{i-1}), \max(a_i, a_{i-1})\right]

时，

|d_i|\gets |d_i|+v

。

将询问离线并且按

u

升序排序，对

u

扫描线。随着

u

的增大，每个

d_i

会在不变和加

v

之间切换。

我们可以用开四个数据结构，维护不变的正差分

P_0

，加

v

的正差分

P_1

，不变的负差分

N_0

，减

v

的负差分

N_1

。扫描线的过程中容易更新这四个集合。

需要查询

x

中前

k

大数的和。可以视为对

P_1

打一个全局加标记

v

以后，查询

P_0 \cup P_1

的前

k

大数之和。对于

y

同理。

可以使用 FHQ-Treap 维护

P_0,P_1,N_0,N_1

，支持插入删除和并集查询。由于外层需要三分，复杂度为

O(q \log^2 n)

。代码改成了二分。

CPP

int n, m, q, a[N], d[N], ans[N];
mt19937 rand32(chrono::steady_clock::now().time_since_epoch().count());

struct node {
    node *ls, *rs;
    int size, val, sum;
    unsigned prio;
    node() : ls(nullptr), rs(nullptr), size(1), val(0), sum(0), prio(rand32()) {}
    node(int x) : ls(nullptr), rs(nullptr), size(1), val(x), sum(x), prio(rand32()) {}
    node* pushup() {
        size = 1, sum = val;
        if (ls) size += ls->size, sum += ls->sum;
        if (rs) size += rs->size, sum += rs->sum;
        return this;
    }
};
int S(node *u) {return u ? u->size : 0;}
void split(node* u, int val, node*& x, node*& y) {
    if (!u) return x = y = nullptr, void();
    if (u->val <= val) x = u, split(u->rs, val, u->rs, y);
    else y = u, split(u->ls, val, x, u->ls);
    u->pushup();
}
node* merge(node* a, node* b) {
    if (!a || !b) return a ? a : b;
    return (a->prio < b->prio)
    ? (a->rs = merge(a->rs, b), a->pushup())
    : (b->ls = merge(a, b->ls), b->pushup());
}

void insert(node*& u, int val) {
    node *x, *y; split(u, val, x, y);
    u = merge(merge(x, new node(val)), y);
}
void remove(node*& u, int val) {
    node *x, *y, *z;
    split(u, val, x, z), split(x, val - 1, x, y);
    if (y) y = merge(y->ls, y->rs);
    u = merge(merge(x, y), z);
}
int kth(node* u, int k) {
    while (u) {
        if (k == S(u->rs) + 1) return u->val;
        if (k <= S(u->rs)) u = u->rs;
        else k -= S(u->rs) + 1, u = u->ls;
    } return 0;
}
int sum(node* u, int k) {
    int res = 0;
    while (u && k > 0) {
        if (k <= S(u->rs)) u = u->rs;
        else res += (u->rs ? u->rs->sum : 0) + u->val, k -= S(u->rs) + 1, u = u->ls;
    } return res;
}
int kth(node* u1, int v1, node* u2, int v2, int k) {
    if (!u1) return kth(u2, k) + v2;
    if (!u2) return kth(u1, k) + v1;
    if (k <= 0) return 0;
    int w1 = u1->val + v1, w2 = u2->val + v2;
    if (w1 < w2) swap(u1, u2), swap(v1, v2);
    int s1 = S(u1->rs), s2 = S(u2->rs);
    return k <= s1 + s2 + 1 ? kth(u1, v1, u2->rs, v2, k) : kth(u1->ls, v1, u2, v2, k - s1 - 1);
}
int sum(node* u1, int v1, node* u2, int v2, int k) {
    if (!u1) return sum(u2, k) + v2 * k;
    if (!u2) return sum(u1, k) + v1 * k;
    if (k <= 0) return 0;
    int w1 = u1->val + v1, w2 = u2->val + v2;
    if (w1 < w2) swap(u1, u2), swap(v1, v2);
    int s1 = S(u1->rs), s2 = S(u2->rs);
    if (k <= s1 + s2 + 1) return sum(u1, v1, u2->rs, v2, k);
    int p = (u1->rs ? u1->rs->sum : 0) + u1->val + v1 * (s1 + 1);
    return p + sum(u1->ls, v1, u2, v2, k - s1 - 1);
}

node *P0, *P1, *N0, *N1;
vector<tuple<int, int, int>> qry;   // [u, v, id]
vector<tuple<int, int, int>> line;  // [u, type, pos]

void prework() {
    P0 = P1 = N0 = N1 = nullptr;
    for (int i = 1; i <= n + 1; i++) {
        d[i] = a[i] - a[i - 1];
        int x = min(a[i], a[i - 1]), y = max(a[i], a[i - 1]);
        if (x < y) line.emplace_back(x + 1, 1, i), line.emplace_back(y + 1, -1, i);
        if (d[i] > 0) insert(P0, d[i]);
        else insert(N0, -d[i]);
    }
    sort(line.begin(), line.end());
}
void update(int x) {
    auto [u, type, pos] = line[x];
    if (d[pos] > 0) {
        if (type == 1) remove(P0, d[pos]), insert(P1, d[pos]);
        else remove(P1, d[pos]), insert(P0, d[pos]);
    } else {
        if (type == 1) remove(N0, -d[pos]), insert(N1, -d[pos]);
        else remove(N1, -d[pos]), insert(N0, -d[pos]);
    }
}
 
void _main() {
    cin >> n >> m >> q;
    for (int i = 1; i <= n; i++) cin >> a[i];
    for (int i = 1, u, v; i <= q; i++) {
        cin >> v >> u;
        qry.emplace_back(u, v, i);
    }
    sort(qry.begin(), qry.end());
    prework();
    int p = 0, lim = line.size();
    for (const auto& [u, v, id] : qry) {
        while (p < lim && get<0>(line[p]) <= u) update(p++);
        int l = 0, r = min(S(P0) + S(P1), S(N0) + S(N1)), k = 0; 
        while (l <= r) {
            int mid = (l + r) >> 1;
            if (mid == 0) {l = 1; continue;}
            int x = kth(P0, 0, P1, v, mid), y = kth(N0, 0, N1, v, mid);
            if (x + y > m + v) k = mid, l = mid + 1;
            else r = mid - 1;
        }
        int x = sum(P0, 0, P1, v, k), y = sum(N0, 0, N1, v, k);
        int tot = (P0 ? P0->sum : 0) + (P1 ? P1->sum : 0) + S(P1) * v
                  + (N0 ? N0->sum : 0) + (N1 ? N1->sum : 0) + S(N1) * v;
        ans[id] = tot + 2 * k * (m + v) - 2 * (x + y);
    }
    for (int i = 1; i <= q; i++) cout << ans[i] / 2 << '\n';
}

6.10 WC2025 T3

P11630 [WC2025] 士兵。

给出 $n$ 个二元组 $(a_i,b_i)$ ，一次操作支付 $m$ 的代价，将一个区间上的所有 $a_i$ 减 $1$ 。所有操作结束后，你的得分为 $\sum\limits_{i=1}^n b_i[a_i \le 0]$ 。

最大化得分减去代价的值。

多测， $\sum n \le 5 \times 10^5$ ， $1 \le a_i,m \le 10^9$ ， $-10^9 \le b_i \le 10^9$ 。2 秒，1024 MB。

题解

根据 2.1 给出的构造，我们任意赋一组非负整数

x_i

表示第

i

个位置被操作的次数，总能找到一种方案。这时的最小操作次数为

\sum \limits_{i=1}^n \max(0,x_i-x_{i-1})

。

写出答案式子为

\sum _{i=1}^n b_i[x_i \ge a_i]-m\sum _{i=1}^n \max(0,x_i-x_{i-1})\\ =\sum_{i=1}^n \left(b_i[x_i \ge a_i]-m \times \max(0,x_i-x_{i-1})\right)

容易把贡献拆到每个位置

i

上。据此设计一个 DP，令

f_{i,j}

表示考虑前

i

个元素，满足

x_i=j

时前缀的最大得分，转移是平凡的，做到

O(nV)

。这个东西很难优化，所以需要先把状态压下来。

进一步，考察操作的性质。注意到令

x_i \gets x_{i-1}

总能避免

m

的代价。考虑

x_i

序列的形态，则其仅在特定位置产生突变。具体地：

当 $b_i>0$ 时，有决策 $x_i \gets a_i$ ，获得 $b_i$ 的得分。
当 $b_i<0$ 时，有决策 $x_i \gets a_i-1$ ，避免 $-b_i$ 的代价。

此时我们并不需要记录

O(V)

种决策，直接将状态改为：

f_i

表示考虑前

i

个元素，且

i

处产生突变的最大得分。我们记

c_i=a_i-[b_i<0]

，则

f_i

是原本的

f_{i,c_i}

。

枚举上一个突变点

j

，此时

\forall k \in [j,i), x_i \gets c_j

。二者之间产生

m \times \max(0,c_i-c_j)

的代价。同时我们需要枚举

k \in (j,i)

判断这些点是否被顺带消除，得到式子：

f_i=\max(0,b_i)+\max_{j=0}^{i-1} \left(f_j - m \times \max(0,c_i-c_j) +\sum_{k=j+1}^{i-1} b_k [c_i \ge a_k] \right)

倒序枚举

j

即可动态维护后面那个求和式，做到

O(n^2)

，获得 35pts。

CPP

int n, m, a[N], b[N], c[N], f[N];
void _main() {
	cin >> n >> m;
	for (int i = 1; i <= n; i++) cin >> a[i] >> b[i], c[i] = a[i] - (b[i] < 0);
	fill(f + 1, f + n + 1, -1e18);
	for (int i = 1; i <= n; i++) {
		int v = 0;
		for (int j = i - 1; j >= 0; j--) {
			f[i] = max(f[i], max(0LL, b[i]) + f[j] - m * max(0LL, c[i] - c[j]) + v);
			if (c[i] >= a[j]) v += b[j];
		}
	}
	cout << *max_element(f, f + n + 1) << '\n';
}

令

h(l,r)=\sum\limits_{k=l+1}^{r-1} b_k [c_r \ge a_k]

。注意到转移式中有

\max(0,c_i-c_j)

这个东西，考虑分类讨论：

若 $c_j \ge c_i$ ，此时无消除代价，我们需要查询 $c_j \in [c_i,+\infty)$ 的最大得分 $f_j+h(j,i)$ 。
若 $c_j < c_i$ ，此时支付 $m(c_i-c_j)$ 的代价，我们需要查询 $c_j \in [0,c_i]$ 的最大得分 $f_j+m\times c_j+h(j,i)$ 。

离散化以后，将两棵线段树建在

c_i

上，分别维护两种情况，需要支持区间加、区间 chkmax，复杂度

O(n \log n)

。

CPP

int n, m, len, a[N], b[N], c[N], d[N << 1];
int idx(int x) {return lower_bound(d + 1, d + len + 1, x) - d;}

struct segtree {
#define ls (rt << 1)
#define rs (rt << 1 | 1)
	constexpr static int inf = 1e18;
	int val[N << 3], add[N << 3], cmax[N << 3];
	void pushup(int rt) {val[rt] = max(val[ls], val[rs]);}
	void apply(int rt, int ad, int cm) {
		val[rt] = max(val[rt] + ad, cm), add[rt] += ad;
		cmax[rt] = max(cmax[rt] + ad, cm);
	}
	void pushdown(int rt) {
		apply(ls, add[rt], cmax[rt]), apply(rs, add[rt], cmax[rt]), add[rt] = 0, cmax[rt] = -inf;
	}
	void build(int l = 0, int r = len, int rt = 1) {
		add[rt] = 0, cmax[rt] = -inf, val[rt] = -inf;
		if (l == r) return;
		int mid = (l + r) >> 1;
		build(l, mid, ls), build(mid + 1, r, rs);
	}
	void uadd(int tl, int tr, int c, int l = 0, int r = len, int rt = 1) {
		if (tl <= l && r <= tr) return apply(rt, c, -inf), void();
		int mid = (l + r) >> 1;
		pushdown(rt);
		if (tl <= mid) uadd(tl, tr, c, l, mid, ls);
		if (tr > mid) uadd(tl, tr, c, mid + 1, r, rs);
		pushup(rt);
	}
	void umax(int tl, int tr, int c, int l = 0, int r = len, int rt = 1) {
		if (tl <= l && r <= tr) return apply(rt, 0, c), void();
		int mid = (l + r) >> 1;
		pushdown(rt);
		if (tl <= mid) umax(tl, tr, c, l, mid, ls);
		if (tr > mid) umax(tl, tr, c, mid + 1, r, rs);
		pushup(rt);
	}
	int ask(int x, int l = 0, int r = len, int rt = 1) {
		if (l == r) return val[rt];
		int mid = (l + r) >> 1;
		pushdown(rt);
		return x <= mid ? ask(x, l, mid, ls) : ask(x, mid + 1, r, rs);
	}
} T1, T2;

void _main() {
	cin >> n >> m, len = 0;
	for (int i = 1; i <= n; i++) {
		cin >> a[i] >> b[i], c[i] = a[i] - (b[i] < 0);
		d[++len] = a[i], d[++len] = a[i] - 1;
	}
	sort(d + 1, d + len + 1), len = unique(d + 1, d + len + 1) - d - 1;
	T1.build(), T2.build();
	T1.umax(0, 0, 0), T2.umax(0, len, 0);
	for (int i = 1; i <= n; i++) {
		int v1 = T1.ask(idx(c[i])), v2 = T2.ask(idx(c[i])) - m * c[i];
		int v = max(v1, v2) + max(0LL, b[i]);
		T1.uadd(idx(a[i]), len, b[i]), T2.uadd(idx(a[i]), len, b[i]);
		T1.umax(0, idx(c[i]), v), T2.umax(idx(c[i]), len, v + m * c[i]);
	} cout << T1.val[1] << '\n';
}

6.11 一道模拟赛题

某场模拟赛的题目。

给出一棵树，每个点有点权 $a_i$ ，每条边有边权。一次操作花费 $a_u+a_v$ 的代价，将从 $u$ 到 $v$ 的简单路径上所有边权减 $1$ 。要求操作过程中边权非负。

给出 $q$ 次修改，每次修改给出 $(u,v,w)$ ，将从 $u$ 到 $v$ 的简单路径上所有边权加上 $w$ 。在每次修改结束后，求出使得所有边权变为 $0$ 的最小操作次数。

$n, q \times 2 \times 10^5$ 。3 秒，512 MB。

题解

考虑 4.1 的插头法。对于点

u

，我们记

S_u=\sum \limits_{(u,v,w) \in E} w\\ M_u=\max \limits_{(u,v,w) \in E} w

对于延伸到

u

的插头，我们希望插头尽量合并。注意到有过多插头来自同一个

v

时，同一来源的插头可能无法全部配对。

当 $2M_u>S_u$ 时，我们必须新建 $2M_u-S_u$ 个插头。这也是 6.4 得到的结论。
当 $2M_u \le S_u$ 时，则我们可以完成 $\left\lfloor \dfrac{S_u}{2} \right\rfloor$ 次插头配对。此时新建 $S_u \bmod 2$ 个插头。

将贡献乘上点权即可得到答案：

CPP

int solve() {
    int res = 0;
    for (int u = 1; u <= n; u++) {
        int sum = 0, mx = 0;
        for (auto [v, w] : e[u]) sum += w, mx = max(mx, w);
        if (2 * mx > sum) res += (2 * mx - sum) * a[u];
        else if (sum & 1) res += a[u];
    } return res;
}

进一步，考虑用数据结构维护上述过程。将树重链剖分后，我们将点分为三类：

A 类点：满足 $2M_u>S_u$ 且 $M_u$ 位于重链上；
B 类点：满足 $2M_u>S_u$ 且 $M_u$ 位于轻儿子中；
C 类点：满足 $2M_u \le S_u$ 。

对于一次修改，除去路径端点以后其余点都有两条邻边被修改。

对于 A 类点，我们发现其贡献是 $2(M_u+w)-(S_u+2w)=2M_u-S_u$ ，不变。
对于 B 类点，其贡献变为 $2M_u-(S_u+2w)=2M_u-S_u-2w$ 。若贡献为负，则其变为一个 C 类点。
对于 C 类点，若 $S_u \gets S_u + 2w$ ， $M_u$ 最多变为 $M_u+w$ ，故其仍然满足 $2M_u \le S_u$ 。且 $S_u \bmod 2$ 不改变，其贡献不变。

因此，只需维护 B 类点的贡献。

我们建立一棵线段树维护如下信息：

重儿子、父亲、轻儿子的边权；
当前节点的点权和 $S_u$ ；
B 类点的贡献和；
当前节点内是否存在 B 类点，B 类点贡献的最小值；
当前节点的答案。

其余的一些信息可以合并，使用懒标记维护。另一些信息则需要重构处理。

在每次修改结束后，重构整棵线段树，若子树不存在 B 类点或 B 类点贡献最小值为正，结束递归。

可以势能分析说明该策略是

O(q \log^2 n)

的。

CPP

#define int long long
const int N = 2e5 + 5, inf = 1e18;
int n, q, a[N];
vector<pair<int, int>> e[N];

int dn, fa[N], dep[N], sz[N], son[N], top[N], dfn[N], rev[N], ef[N], light[N], sum[N];
void dfs1(int u) {
	sz[u] = 1;
	for (auto [v, w] : e[u]) {
		sum[u] += w;
		if (v == fa[u]) continue;
		dep[v] = dep[u] + 1, fa[v] = u, ef[v] = w, dfs1(v), sz[u] += sz[v];
		if (sz[v] > sz[son[u]]) son[u] = v;
	}
}
void dfs2(int u, int t) {
	top[u] = t, dfn[u] = ++dn, rev[dn] = u;
	if (son[u]) dfs2(son[u], t);
	for (auto [v, w] : e[u]) {
		if (v != fa[u] && v != son[u]) dfs2(v, v), light[u] = max(light[u], w);
	}
}

struct node {
	int son, fa, light;  // 重儿子边权、返祖边边权、轻儿子边权最大值
	int w;               // 点权
	int sum;             // S_u
	int val;             // 答案
	int sumb;            // B 类点贡献和
	int mn;              // B 类点贡献最小值
	bool B;              // 是否存在 B 类点
	void rebuild() {   // 重构
		int m = max({son, fa, light});
		if (2 * m <= sum) return B = false, val = (sum & 1) * w, sumb = 0, mn = inf, void();
		val = (2 * m - sum) * w;
		if (m > son && m > fa) B = true, sumb = w, mn = 2 * m - sum;
		else B = false, sumb = 0, mn = inf;
	}
};
node make(int u) {
	node x;
	x.fa = ef[u], x.son = ef[son[u]], x.light = light[u];
	x.w = a[u], x.sum = sum[u];
	return x.rebuild(), x;
}

struct segtree {
#define ls (rt << 1)
#define rs (rt << 1 | 1)
	node val[N << 2];
	int tag[N << 2];
	void pushup(int rt) {
		val[rt].sumb = val[ls].sumb + val[rs].sumb, val[rt].val = val[ls].val + val[rs].val;
		val[rt].B = val[ls].B | val[rs].B, val[rt].mn = min(val[ls].mn, val[rs].mn);
	}
	void apply(int rt, int x) {
		tag[rt] += x;
		if (val[rt].B) val[rt].val -= 2 * x * val[rt].sumb, val[rt].mn -= 2 * x;
		val[rt].sum += 2 * x, val[rt].son += x, val[rt].fa += x;
	}
	void pushdown(int rt) {
		if (!tag[rt]) return;
		apply(ls, tag[rt]), apply(rs, tag[rt]), tag[rt] = 0;
	}
	void add(int tl, int tr, int c, int l = 1, int r = n, int rt = 1) {
		if (tl <= l && r <= tr) return apply(rt, c), void();
		int mid = (l + r) >> 1;
		pushdown(rt);
		if (tl <= mid) add(tl, tr, c, l, mid, ls);
		if (tr > mid) add(tl, tr, c, mid + 1, r, rs);
		pushup(rt); 
	}
	void maintain(int l = 1, int r = n, int rt = 1) {
		if (!val[rt].B || val[rt].mn >= 0) return;
		if (l == r) return val[rt].rebuild();
		int mid = (l + r) >> 1;
		pushdown(rt), maintain(l, mid, ls), maintain(mid + 1, r, rs), pushup(rt);
	}
	void ason(int x, int c, int l = 1, int r = n, int rt = 1) {
		if (l == r) return val[rt].son += c, val[rt].sum += c, val[rt].rebuild();
		int mid = (l + r) >> 1;
		pushdown(rt);
		if (x <= mid) ason(x, c, l, mid, ls);
		else ason(x, c, mid + 1, r, rs);
		pushup(rt);
	}
	void afa(int x, int c, int l = 1, int r = n, int rt = 1) {
		if (l == r) return val[rt].fa += c, val[rt].sum += c, val[rt].rebuild();
		int mid = (l + r) >> 1;
		pushdown(rt);
		if (x <= mid) afa(x, c, l, mid, ls);
		else afa(x, c, mid + 1, r, rs);
		pushup(rt);
	}
	void ulight(int x, int d, int v, int l = 1, int r = n, int rt = 1) {
		if (l == r) return val[rt].light = max(val[rt].light, v), val[rt].sum += d, void();
		int mid = (l + r) >> 1;
		pushdown(rt);
		if (x <= mid) ulight(x, d, v, l, mid, ls);
		else ulight(x, d, v, mid + 1, r, rs);
		pushup(rt);
	}
	node ask(int x, int l = 1, int r = n, int rt = 1) {
		if (l == r) return val[rt];
		int mid = (l + r) >> 1;
		pushdown(rt);
		return x <= mid ? ask(x, l, mid, ls) : ask(x, mid + 1, r, rs);
	}
	int all() {return val[1].val;}
	void build(int l = 1, int r = n, int rt = 1) {
		if (l == r) return val[rt] = make(rev[l]), void();
		int mid = (l + r) >> 1;
		build(l, mid, ls), build(mid + 1, r, rs), pushup(rt), val[rt].w = val[ls].w + val[rs].w;
	}
} sgt;

void change(int u, int v, int c) {
	while (top[u] != top[v]) {
		if (dep[top[u]] < dep[top[v]]) swap(u, v);
		if (u != top[u]) sgt.add(dfn[top[u]], dfn[u] - 1, c);
		sgt.afa(dfn[u], c);
		int v = sgt.ask(dfn[top[u]]).fa;
		u = fa[top[u]];
		sgt.ulight(dfn[u], c, v);
	}
	if (dep[u] < dep[v]) swap(u, v);
	if (u == v) sgt.ason(dfn[u], 0);
	else sgt.add(dfn[son[v]], dfn[fa[u]], c), sgt.afa(dfn[u], c), sgt.ason(dfn[v], c);
	sgt.maintain();
}

void _main() {
	cin >> n >> q;
	for (int i = 1; i <= n; i++) cin >> a[i];
	for (int i = 1, u, v, w; i < n; i++) {
		cin >> u >> v >> w;
		e[u].emplace_back(v, w), e[v].emplace_back(u, w);
	}
	dfs1(1), dfs2(1, 1), sgt.build();
	cout << sgt.all() << '\n';
	for (int u, v, w; q--; ) {
		cin >> u >> v >> w;
		change(u, v, w), cout << sgt.all() << '\n';
	}
}

6.12 CF1884E

CF1884E Hard Design：

给定长为 $n$ 的序列 $a_i$ ，一次操作花费 $(r-l+1)^2$ 的代价，将 $[l,r]$ 中的数字减去 $1$ 。

对 $a$ 的所有循环位移求出：使所有数字都相等的最小操作次数。在此基础上，求出最小代价。

多测， $\sum n \le 10^6$ ，3 秒，250 MB。

题解

不难发现所有数字都变成最大值时，操作次数最小。

设最大值为

M

，令

a_i \gets M-a_i

，问题就转化为序列铲雪。由 2.1 的结论得到第一问答案

\sum_{i=1}^n \max(0,a_i-a_{i-1})

该值可以在循环位移过程中方便地维护。

对于第二问，我们则使用 2.2 的插头法。假设已处理完左侧，当前位于位置

i

，左侧传来的右插头数量为

k

，作如下讨论：

若 $k \ge a_i$ ：所有插头均可在此处被使用。每个插头贡献的长度为 $i-p_x+1$ ，因此代价为

\sum_{x=1}^k (i-p_x+1)^2=k(i+1)^2+\sum_{x=1}^k {p_x}^2-2(i+1)\sum_{x=1}^k p_x

处理完毕后，

k \gets k-a_i

，且剩余插头的起点均变为

i

。

若 $k < a_i$ ：此时需要额外创建 $a_i-k$ 个插头，这些插头的起点就是 $i$ 。我们还需决定 $k$ 个已有插头中哪些与当前的 $a_i$ 配对。

根据直觉，越靠前的插头优先配对，得到的代价越小。

考虑证明这一观察。不妨考虑二元情况，即两个插头配对两个点的情况。

设两个插头的起点为 $a,b$ ，当前处理位置为 $c$ ，之后存在另一配对点 $d$ 。则 $a<b<c<d$ 。要证 $(b-c)^2+(a-d)^2>(a-c)^2+(b-d)^2$ ，即证
$\begin{aligned} (b-c)^2+(a-d)^2-(a-c)^2-(b-d)^2 &> 0\\ bc+ad-ac-bd &> 0\\ a(d-c)+b(c-d) &> 0\\ (b-a)(d-c) &> 0\\ \end{aligned}$
上式显然成立。

因此，应将最靠前的

a_i

个插头在此处用完，其代价为

\sum_{x=1}^{a_i} (i-p_x+1)^2=a_i(i+1)^2+\sum_{x=1}^{a_i} {p_x}^2-2(i+1) \sum_{x=1}^{a_i} p_x

处理完毕后，

k \gets k - a_i

，并删除

p

中的前

a_i

个起点。

综上所述，我们需要一种数据结构维护插头起点集合

p

，支持前缀删除、前缀和以及前缀平方和查询。使用平衡树即可

O(n\log n)

算出序列每个前缀的最小代价。

进一步，由于转化后

a

中至少有一个

0

，我们选择任意一个

0

作为起点将环断开成链。因为没有任何操作会跨过这个断点，因此链上计算的代价就是整个环的代价。

从断点向左和向右做两次扫描，处理出序列的前缀代价和后缀代价。将结果合并，即可得到完整答案。

CPP

#define int long long
const int N = 1e6 + 5;

mt19937 rand32(chrono::steady_clock::now().time_since_epoch().count());
struct node {
	unsigned prio;
	node *ls, *rs;
	int start, cnt, sum;
	mint x, x2;
	node(int a = 0, int b = 0) 
	: prio(rand32()), ls(nullptr), rs(nullptr), start(a), 
	  cnt(b), sum(b), x((mint)a * b), x2((mint)a * a * b) {}
	node* pushup() {
		sum = cnt, x = (mint)start * cnt, x2 = (mint)start * start * cnt;
		if (ls) sum += ls->sum, x += ls->x, x2 += ls->x2;
		if (rs) sum += rs->sum, x += rs->x, x2 += rs->x2;
		return this;
	}
	mint calc(mint pos) {return pos * pos * sum - x * pos * 2 + x2;}
};
node* merge(node* u, node* v) {
	if (!u || !v) return u ? u : v;
	return (u->prio < v->prio) ?
	(u->rs = merge(u->rs, v), u->pushup()) :
	(v->ls = merge(u, v->ls), v->pushup());
}
void split(node* u, int k, node*& x, node*& y) {
	if (!u) return x = y = nullptr, void();
	int ls = u->ls ? u->ls->sum : 0;
	if (k <= ls) {
		y = u, split(u->ls, k, x, u->ls), u->pushup();
	} else if (k < ls + u->cnt) {
		y = new node(u->start, u->cnt - k + ls), y->rs = u->rs, y->pushup();
		u->cnt = k - ls, x = u, u->rs = nullptr, u->pushup();
	} else {
		x = u, split(u->rs, k - ls - u->cnt, u->rs, y), u->pushup();
	}
}

int n, a[N];
pair<int, mint> pre[N], suf[N];

void solve(int n, pair<int, mint>* ans) {
	node *rt = nullptr;
	int cnt = 0; mint cost = 0;
	for (int i = 1; i < n; i++) {
		cnt += max(0LL, a[i] - a[i - 1]);
		int ln = rt ? rt->sum : 0;
		if (a[i] > ln) {
			rt = merge(rt, new node(i, a[i] - ln));
		} else if (a[i] < ln) {
			node *x, *y; split(rt, a[i], x, y);
			cost += y ? y->calc(i) : 0, rt = x;
		}
		ans[i] = {cnt, cost + (rt ? rt->calc(i + 1) : 0)};
	}
}

void _main() {
	cin >> n;
	for (int i = 0; i < n; i++) cin >> a[i];
	if (n == 1) return cout << "0 0\n", void();
	int rot = max_element(a, a + n) - a, m = a[rot];
	rotate(a, a + rot, a + n);
	for (int i = 0; i < n; i++) a[i] = m - a[i];
	solve(n, pre);
	reverse(a + 1, a + n), solve(n, suf), reverse(suf + 1, suf + n);
	for (int i = 0; i < n; i++) {
		int k = (i - rot + n) % n, cnt = 0; mint cost = 0;
		if (k > 0) cnt += suf[k].first, cost += suf[k].second;
		if (k > 1) cnt += pre[k - 1].first, cost += pre[k - 1].second;
		if (k == 0) cnt += pre[n - 1].first, cost += pre[n - 1].second;
		cout << cnt << ' ' << cost << '\n';
	} 
}

参考资料

1.3 线性规划基础——OI Wiki。
3.2 [ARC136C] Circular Addition 题解——braveTester。
4.1 P7246 手势密码——Alex_Wei。
6.4 题解 AT2304 【[AGC010C] Cleaning】——zhylj。

本文的 markdown 源码恰为 $2026$ 行。

十二重铲雪法

文章操作

前言

约定

铲雪模型

1. 前置知识

1.1 差分

1.2 笛卡尔树

1.3 对偶原理

2. 序列铲雪

2.1 差分法

2.2 插头法

2.3 笛卡尔树法

2.4 线性规划法

3. 环上铲雪

3.1 差分法

3.2 插头法

3.3 线性规划法

4. 树上铲雪

4.1 插头法

4.2 线性规划法

5. 基环树铲雪

5.1 线性规划法

6. 练习

6.1 单点清空铲雪

6.2 CF1954E

6.3 环上铲雪·构造

6.4 AGC010C

6.5 跳跃铲雪

6.6 限长铲雪

6.7 二元铲雪

6.8 循环铲雪

6.9 循环铲雪·改

6.10 WC2025 T3

6.11 一道模拟赛题

6.12 CF1884E

参考资料

相关推荐

评论

十二重铲雪法