题解：P14255 列车（train）

通过简单推理得出以下结论：

下面用节点编号指代节点。

结论1：若存在一条

i

到达

j

的通路，则对于所有的

k>j

存在一条

i

到达

k

的通路。

证明：若存在一条

i

到达

j

的通路，且存在一个

k>j

满足没有从

i

到

k

的通路，则一定有一个修改操作

[l,r]

满足

l \leq i

且

k \leq r

，而因为

i < j < k

所以本次修改操作必定会断掉

i

到

j

的通路，与假设矛盾。

所以我们设

nxt_i

表示

i

右边第一个存在一条和

i

相连的通路的节点，初值为

nxt_i = i + 1

，发现每次修改操作相当于将

[l,r]

中所有的节点的

nxt

值对

r + 1

取

max

。

故我们得出结论2：

nxt

单调不降。

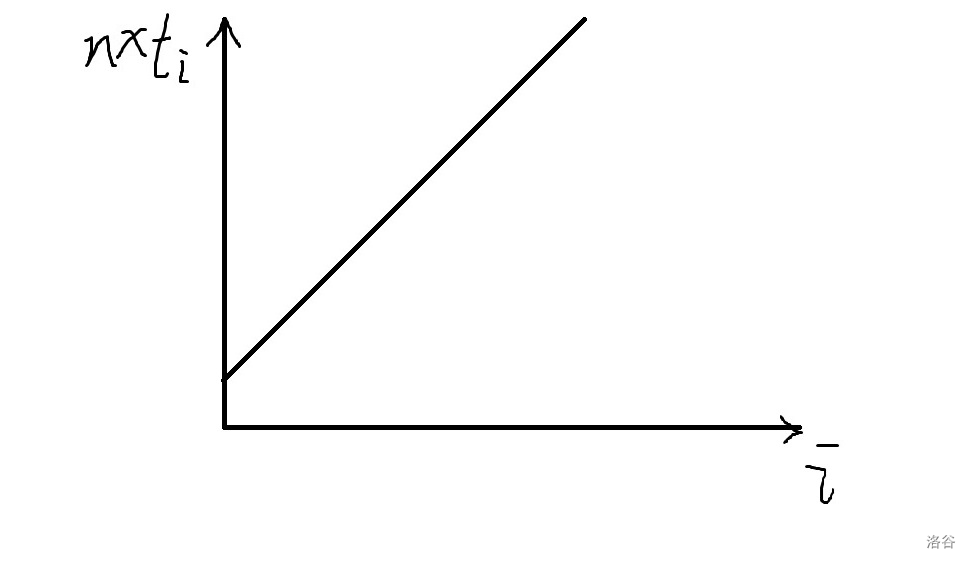
这个可以画图理解一下，将

i

作为横轴

nxt_i

作为纵轴，初始就是一条斜线，每次修改相当于把一段区间抬升至右端点。

下面是示意图。

这是修改前。

这是第一次修改后。

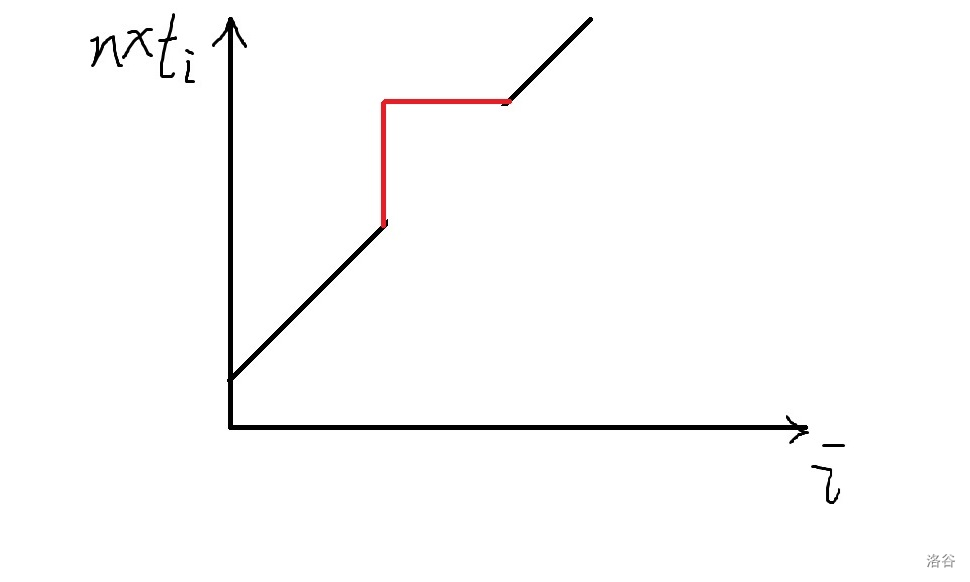
后面也是类似的。

有了以上结论我们就可以开始做题了。

对于

nxt

建个线段树维护它，每次就是线段树上二分出最后一个

nxt_x<r + 1

的

x

，然后将

[l,x]

更新成

r + 1

，注意判掉

x<l

之类的边界情况。可能有些读者会认为先二分再推平的操作比较愚蠢，不如直接区间取最大值，但是其实这是为下面的步骤做准备。

对于查询操作。

我们发现有两种可能到达

r

的方式，一种是

x \leq l

且

nxt_x < r

，这个情况的最小费用是

p_r - p_x

，一种是

x \leq l

且

r \leq nxt_x

，这个情况的最小费用是

p_{nxt_x} - p_x

，我们线段树上二分出

nxt_x < r

的分界点，把两种分开处理。

第一种的处理是简单的，显然取合法的最右端的点

x

的费用

p_r-p_x

，下面主要讲第二种情况。

我们建一棵线段树表示维护

p_{nxt_i} - p_i

的最小值，在区间赋值时，找到线段树上要更新的点时，设这个点维护

[L,R]

内的信息，我们发现整个区间的

nxt_i

都是相同的，设要更新成的值为

s

，最小值更新为

p_s-p_R

即可。

以上就是全过程，注意特判

nxt_i > n

之类的情况。

\large{Code}

CPP

#include <bits/stdc++.h>
#define inf 235437085470998
using namespace std;

inline long long read(void) {
	long long x = 0, f = 1;
	char c = getchar();
	while (c > '9' || c < '0') {
		if (c == '-') f = -1;
		c = getchar();
	}
	while (c >= '0' && c <= '9') x = (x << 1) + (x << 3) + c - 48, c = getchar();
	return x * f;
}

long long T, n, m, t, p[100005], tree[2000000], tree2[2000000], tag[2000000], opt, nl, nr;

void pushdown (long long x, long long l, long long r) {
	if (tag[x] && l < r) {
		long long mid = l + r >> 1;
		tree[x << 1] = tag[x], tree[x << 1 | 1] = tag[x];
		tree2[x << 1] = p[tag[x]] - p[mid], tree2[x << 1 | 1] = p[tag[x]] - p[r];
		tag[x << 1] = tag[x << 1 | 1] = tag[x];
		tag[x] = 0;
	}
}

void upd (long long x, long long l, long long r, long long ql, long long qr, long long s) {
	if (l == ql && r == qr) {
		tree[x] = s, tree2[x] = p[s] - p[r], tag[x] = s;
		return;
	}
	pushdown(x, l, r);
	long long mid = l + r >> 1;
	if (qr <= mid) upd(x << 1, l, mid, ql, qr, s);
	else if (ql > mid) upd(x << 1 | 1, mid + 1, r, ql, qr, s);
	else upd(x << 1, l, mid, ql, mid, s), upd(x << 1 | 1, mid + 1, r, mid + 1, qr, s);
	tree[x] = min(tree[x << 1], tree[x << 1 | 1]), tree2[x] = min(tree2[x << 1], tree2[x << 1 | 1]);
}

long long find (long long x, long long l, long long r, long long s) {
	if (tree[x] >= s) return 0;
	if (l == r) return l;
	pushdown(x, l, r);
	long long mid = l + r >> 1;
	if (tree[x << 1 | 1] >= s) return find(x << 1, l, mid, s);
	else return find(x << 1 | 1, mid + 1, r, s);
}

long long query (long long x, long long l, long long r, long long ql, long long qr) {
	if (l == ql && r == qr) return tree2[x];
	pushdown(x, l, r);
	long long mid = l + r >> 1;
	if (qr <= mid) return query(x << 1, l, mid, ql, qr);
	else if (ql > mid) return query(x << 1 | 1, mid + 1, r, ql, qr);
	else return min(query(x << 1, l, mid, ql, mid), query(x << 1 | 1, mid + 1, r, mid + 1, qr));
}

int main(void) {
	T = read();
	while (T--) {
		n = read(), m = read(), t = 1;
		for (int i = 1; i <= n; i++) p[i] = read();
		p[n + 1] = inf;
		while (t < n) t <<= 1;
		for (int i = t; i < t + n; i++) tree[i] = i - t + 2, tree2[i] = p[i - t + 2] - p[i - t + 1], tag[i] = 0;
		for (int i = t + n; i < t + t; i++) tree[i] = tree2[i] = inf, tag[i] = 0;
		for (int i = t - 1; i >= 1; i--)
			tree[i] = min(tree[i << 1], tree[i << 1 | 1]), tree2[i] = min(tree2[i << 1], tree2[i << 1 | 1]), tag[i] = 0;
		while (m--) {
			opt = read(), nl = read(), nr = read();
			if (opt == 1) {
				long long ans = find(1, 1, t, nr + 1);
				if (ans >= nl) upd(1, 1, t, nl, ans, nr + 1);
			} else {
				long long ans = min(nl, find(1, 1, t, nr + 1));
				if (ans)  {
					long long sum = find(1, 1, t, n + 1);
					sum = min(sum, nl);
					if (ans < sum) printf("%lld\n", min(p[nr] - p[ans], query(1, 1, t, ans + 1, sum)));
					else printf("%lld\n", p[nr] - p[ans]);
				} else {
					long long sum = find(1, 1, t, n + 1);
					sum = min(sum, nl);
					if (sum) printf("%lld\n", query(1, 1, t, 1, sum));
					else puts("-1");
				}
			}
		}
	}
	return 0;
}

题解：P14255 列车（train）

文章操作

相关推荐

评论

题解：P14255 列车（train）