P14636 题解

补题一小时过了，没有学题解的任何东西，因为我看不懂。

考虑原价不取到最大值的情况。如果一个物品可以取到肯定是最优的，因为性价比从大到小排序。但是如果一个物品没钱买可能就会出现问题。

考虑一种情况：按性价比从大到小选，到一个

w_k=2

的物品

k

，刚好剩余一块钱，

k

之前最近选了一个

w_i=1

的物品

i

，

k

之后有一个物品

j

满足

w_j=1

且

w_i+w_j<w_k

。物品的性价比从大到小为

i,k,j

。

按照小 R 的贪心思路，她会先选择

i

。接下来

k

由于需要两块钱，但是只有一块钱没法选，所以小 R 会去选择

j

并把钱花完。但是由于

w_i+w_j<w_k

，用

k

替换

i,j

更优，就会导致贪心出错。

既然是由

i,j,k

引起的贪心出错，那么我们枚举他们三个。注意

j

可能没有，可以认为

j=0

。

考虑

[1,j-1],[j+1,i-1],[i+1,k-1],[k,n]

这四个区间内的

w

应如何选择。

[i+1,k-1]

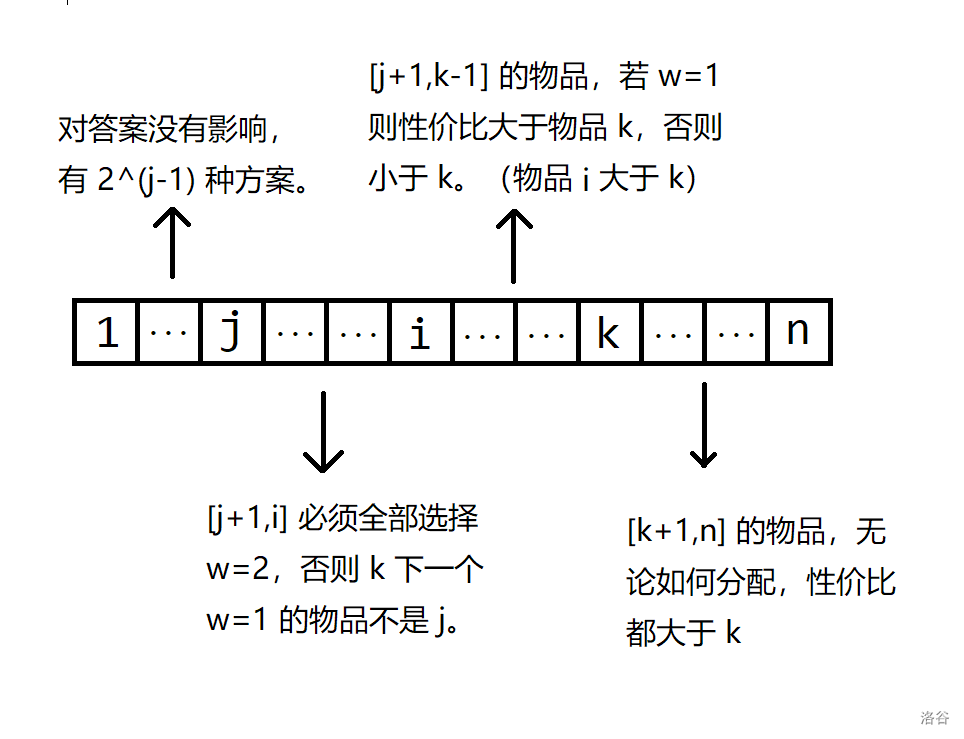
之间物品的权值是不确定的。因此枚举这个区间内

w=1

的个数，设为

x

。方案数为

C_{k-i-1}^x

。

上面这行文字是我赛时没有想到的，赛时以为 $[i+1,k-1]$ 之间全是 $2$ ，sale2.in 调了一辈子，宝宝我真糖。好在想错了还有 $m=2$ 的 $20$ 分保底。

接着对于

[k,n]

之间的物品，还需要花

m-x-2

元（

i

性价比比

k

高，会先选择并花费

1

元）。即在

n-k

个物品中，每个物品有

1/2

的权值，问凑出

m-x-2

的方案数。给权值

-1

，变成

m-x-2-(n-k)

中选择

n-k

个

1

，答案为

C_{m-x-2-(n-k)}^{n-k}

。

其他的在图中已经说清楚了，直接按照前文模拟，时间复杂度

O(Tn^4)

，可以斩获比暴力多过一个测试点

6

的好成绩。

O(Tn^4)

code

CPP

ans=Pow(2,n);
for(int k=2;k<=n;k++)
{
	for(int i=1;i<k;i++)
	{
		if(a[i]*2<=a[k]||m-(n-k)<1) continue;
		for(int j=0;j<i;j++)
		{
			if(a[i]+a[j]>=a[k]) continue;
			for(int x=0;x<=k-i-1&&m-(n-k)-x>=2;x++)
			{
				if(m-(n-k)*2-x>2) continue;
				ans=(ans-Pow(2,j-1)*C[n-k][m-x-2-(n-k)]*C[k-i-1][x])%mod;
			}
		}
	}
}

枚举条件可以不用的，因为不合法的话组合数为

0

。

发现

j

其实是没用的，唯一用处在于

2^{j-1}

。双指针一下就可以去掉

j

的枚举，做到

O(Tn^3)

，理论上

52

，实测

92

。

考虑去掉

x

的枚举。如果你打了上周 ABC，会发现 F 题恰好有这个结论。引用一下原题第一篇题解的 Markdown。

范德蒙德卷积

\sum_{t=0}^{n}\binom{n}{t}\binom{m}{k-t}=\binom{n+m}{k}

证明：考虑一共有

n+m

个物品，从中选

k

个。这件事情等价于在

n

个物品中先选

t

个，再在剩下

m

个物品中选

m-k

个。改变的仅仅是枚举顺序。

代入到

O(Tn^4)

的代码中，就是：

ans=(ans-sum*C[n-j-1][m-2-(n-k)])%mod;

于是就可以做到

O(Tn^2)

。

O(Tn^2)

code

CPP

#include<bits/stdc++.h>
#define int long long
#define mod 998244353
#define N 5005
using namespace std;
int sub,n,m,ans,a[N],C[N][N];
int Pow(int x,int y)
{
	if(y<0) return 0;
	int res=1;
	while(y)
	{
		if(y&1) res=res*x%mod;
		x=x*x%mod;
		y>>=1;
	}
	return res;
}
void solve()
{
	cin>>n>>m;
	for(int i=1;i<=n;i++) cin>>a[i];
	sort(a+1,a+n+1);
	ans=Pow(2,n);
	for(int k=2;k<=n;k++)
	{
		int p=0,sum=1;
		for(int j=k-1;j>=1;j--)
		{
			while(p<n&&a[p+1]<a[k]-a[j]) p++,sum=sum*2%mod;
			if(a[j]*2<=a[k]||m-(n-k)<1||a[j]==a[k]) continue;
			if(m-2-(n-k)>=0&&m-2-(n-k)<=n-j-1) ans=(ans-sum*C[n-j-1][m-2-(n-k)])%mod;
		}
	}
	ans=(ans+mod)%mod;
	cout<<ans<<"\n";
	return;
}
signed main()
{
	ios::sync_with_stdio(0);
	cin.tie(0),cout.tie(0);
	C[0][0]=1;
	for(int i=1;i<=5000;i++)
	{
		C[i][0]=C[i][i]=1;
		for(int j=1;j<i;j++) C[i][j]=(C[i-1][j]+C[i-1][j-1])%mod;
	}
	int t;
	cin>>sub>>t;
	while(t--) solve();
	return 0;
}

事实上我的赛时：T2 调了三小时，操你妈的世界。

文章操作

相关推荐

评论

P14636 题解