题解：CF2045M Mirror Maze

不想写搜索怎么办？来写并查集吧！

\begin{Bmatrix}\color{red}\LARGE\bold{Solution}\\\normalsize\texttt{No.019 }\bold{CF2045M}\end{Bmatrix}\times\footnotesize\texttt{ By Xyz105}

题目描述

给定一个

R

行

C

列的网格。该网格中的每个方格要么为空，要么在方格的一条对角线上有一面镜子。每面镜子由一条线段表示；所有镜子遵循反射定律。

找出所有在网格外沿的位置，满足在该位置放置一个激光发射器，其激光束能击中所有的镜子。如下图所示：

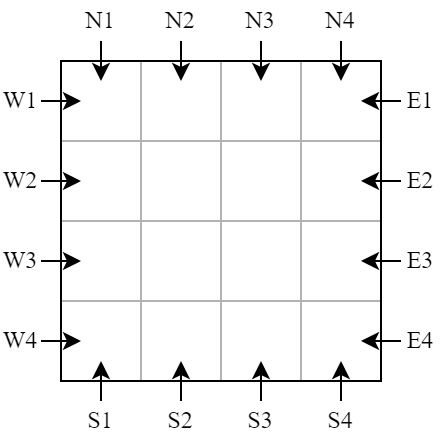
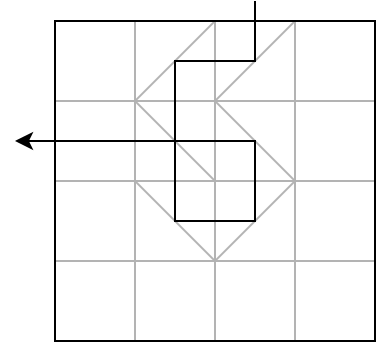
解题思路

记

(i,j,c)

为上数第

i

行左数第

j

列的格子的东/西/南/北边缘，其中

c\isin\{\texttt{E,W,S,N}\}

。不难得出

(i,j,\texttt{S})

与

(i+1,j,\texttt{N})

等价，其它等价式子同理。

对于每个格子

(i,j)

，分类讨论：

若其没有镜子，则连边 $(i,j,\texttt{N})\leftrightarrow(i,j,\texttt{S})$ 和 $(i,j,\texttt{W})\leftrightarrow(i,j,\texttt{E})$ ；
若其镜子方向为左上——右下，则连边 $(i,j,\texttt{N})\leftrightarrow(i,j,\texttt{E})$ 和 $(i,j,\texttt{S})\leftrightarrow(i,j,\texttt{W})$ ；
若其镜子方向为右上——左下，则连边 $(i,j,\texttt{N})\leftrightarrow(i,j,\texttt{W})$ 和 $(i,j,\texttt{S})\leftrightarrow(i,j,\texttt{E})$ 。

使用并查集维护所有连通块，并计算出每个连通块所经过镜子的数量。
具体地，记点

(i,j,c)

的祖先为

fa_{(i,j,c)}

，维护所有

cnt_{(i,j,c)}

（初值为

0

）。对于每个有镜子的格子

(i,j)

，假设镜子方向为左上——右下（反之同理），分类讨论：

若 $fa_{(i,j,\texttt{N})}\neq fa_{(i,j,\texttt{S})}$ ，则令 $cnt_{fa_{(i,j,\texttt{N})}}\gets cnt_{fa_{(i,j,\texttt{N})}}+1,\ cnt_{fa_{(i,j,\texttt{S})}}\gets cnt_{fa_{(i,j,\texttt{S})}}+1$ 。
若 $fa_{(i,j,\texttt{N})}=fa_{(i,j,\texttt{S})}$ ，则仅令 $cnt_{fa_{(i,j,\texttt{N})}}\gets cnt_{fa_{(i,j,\texttt{N})}}+1$ 。

枚举所有在网格外沿的点（形如

(1,i,\texttt{N}),(R,i,\texttt{S}),(i,1,\texttt{W}),(i,C,\texttt{E})

），若其祖先的

cnt

值恰好为镜子总数，则将其输出即可。

参考代码

Submission on Codeforces。

CPP

#include <bits/stdc++.h>
using namespace std;

const int MAXP = 1e5 + 10;

int n, m;

char s[210][210];

int fa[MAXP], cnt[MAXP];

vector<string> ans;

// 1234 = NSWE.
inline int num(int i, int j, int d)
	{return d == 1 ? (i - 1) * m + j :
			d == 2 ? i * m + j : 
			(n + 1) * m + (i - 1) * (m + 1) + j + (d == 4);}

inline int find(int u)
	{return fa[u] == u ? u : fa[u] = find(fa[u]);}
inline void un_(int u, int v)
	{fa[find(u)] = find(v);}

int main()
{
	scanf("%d%d", &n, &m);
	for (int i = 1; i <= n; i++) scanf("%s", s[i] + 1);
	
	for (int i = 1; i < MAXP; i++) fa[i] = i;
	for (int i = 1; i <= n; i++)
		for (int j = 1; j <= m; j++)
		{
			if (s[i][j] == '.')
				un_(num(i, j, 1), num(i, j, 2)), un_(num(i, j, 3), num(i, j, 4));
			else if (s[i][j] == '/')
				un_(num(i, j, 1), num(i, j, 3)), un_(num(i, j, 2), num(i, j, 4));
			else
				un_(num(i, j, 1), num(i, j, 4)), un_(num(i, j, 2), num(i, j, 3));
		}
	int tot = 0;
	for (int i = 1; i <= n; i++)
		for (int j = 1, j1, j2; j <= m; j++)
		{
			if (s[i][j] == '.') continue;
			tot++;
			if (s[i][j] == '/') j1 = num(i, j, 1), j2 = num(i, j, 2);
			else j1 = num(i, j, 1), j2 = num(i, j, 3);
			j1 = find(j1), j2 = find(j2);
			cnt[j1]++; if (j1 != j2) cnt[j2]++;
		}
	
	for (int i = 1; i <= n; i++)
		if (cnt[find(num(i, 1, 3))] == tot) ans.push_back("W" + to_string(i));
	for (int i = 1; i <= n; i++)
		if (cnt[find(num(i, m, 4))] == tot) ans.push_back("E" + to_string(i));
	for (int i = 1; i <= m; i++)
		if (cnt[find(num(1, i, 1))] == tot) ans.push_back("N" + to_string(i));
	for (int i = 1; i <= m; i++)
		if (cnt[find(num(n, i, 2))] == tot) ans.push_back("S" + to_string(i));
	printf("%d\n", ans.size());
	for (auto str : ans) printf("%s ", str.c_str());
	
	return 0;
}

题解：CF2045M Mirror Maze

文章操作

题目描述

解题思路

参考代码

相关推荐

评论

题解：CF2045M Mirror Maze