SP1870 MKLABELS 题解

题目大意

计算给定节点数

N

的树的不同标记方式的数量。这里的“不同标记方式”指的是非同构的标记树的数量，即考虑树的自同构群的影响。

思路分析

这道题可以通过一种非常简单的方法来解决，通过凯莱公式来做。很多人可能连这是什么的不知道，那我们就先来了解一下凯莱公式。

凯莱公式简介

凯莱公式（Cayley`s formula）是组合数学和图论中的一个结论，它给出了告诉我们在

n

个顶点中可以构造多少棵不同的标记树。它是这样一个等式：

\text{有} n \text{个顶点的标记树数量} = n^{n-2}

令

N=\{1,2,\cdots,n\}

为顶点集合，并令

T_n

为有

n

个顶点的标记树的数量。我们可以通过枚举法，在

n

较小时验证此公式，如

T_1=1,T_2=1,T_3=3,T_4=16

。

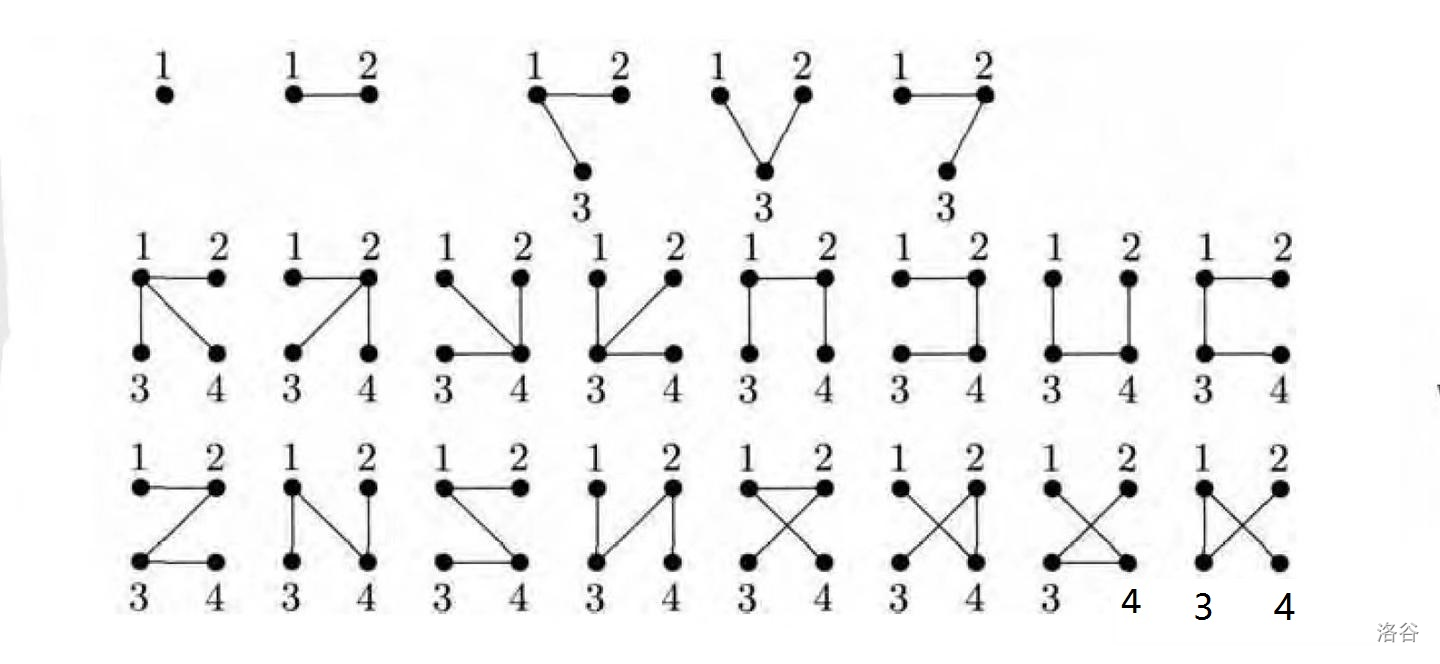
证明这里便不再详细讲述，如果有兴趣可以自己下去查。

相信当你知道了凯莱公式之后，这道题便可以轻松解决了，只需要将凯莱公式带入程序中满足就行了。

参考代码

CPP

#include<bits/stdc++.h>
#define int long long
#define Rint register int
#define fast_running ios::sync_with_stdio(false),std::cin.tie(0),std::cout.tie(0)
using namespace std;

signed main() {
	fast_running;
	int n, cnt = 0;
	while (cin >> n && n != 0) {
		++cnt;
		cout << "Case " << cnt << ", N = " << n << ", # of different labelings = " << (int)(pow(n, n - 2)) << '\n';
		//这里如果用 pow 函数需要强制类型转化，不然可能会用科学计数法输出
		/*也可以这样： 
		int out = pow(n, n - 2);
		cout << out << '\n';
		*/ 
		//当然也可以自己写一个 “pow” 
	}
	return 0;
}

~ 完结撒花 ~

文章操作