Tree Diameter

题意：给定整数

n

，有一棵大小为

n

的树，你需要通过以下两种询问问出树的形态：

给每条边赋 $[1,10^9]$ 的权，求带权直径。
给定两个编号，回答这两条边的距离。

两种操作都不能超过

n

次。

首先，这类问树的形态的题，有一个很常用的思路：一层一层做。

也就是先求出每个点的深度，再一层一层确定树的形态。

由于我们只能知道关于边的信息，所以在边的角度考虑问题。

首先随便取一条边作为根，然后求出每条边的深度，可以通过

n-2

次第二类询问，求出每条边到根的距离。

然后按深度的顺序，一层一层确定树的形态。

首先考虑确定第一层的形态，也就是确定每条边是在左半边还是右半边。

考虑我们可以用第一种操作得到什么信息，可以通过给一个边集的边权整体乘上

\inf

，边集之外的边权设为

1

，这样，求出的结果除以

\inf

下取整就是这个边集的直径。

对于第一层的第一个点，显然接在哪里都是无所谓的。

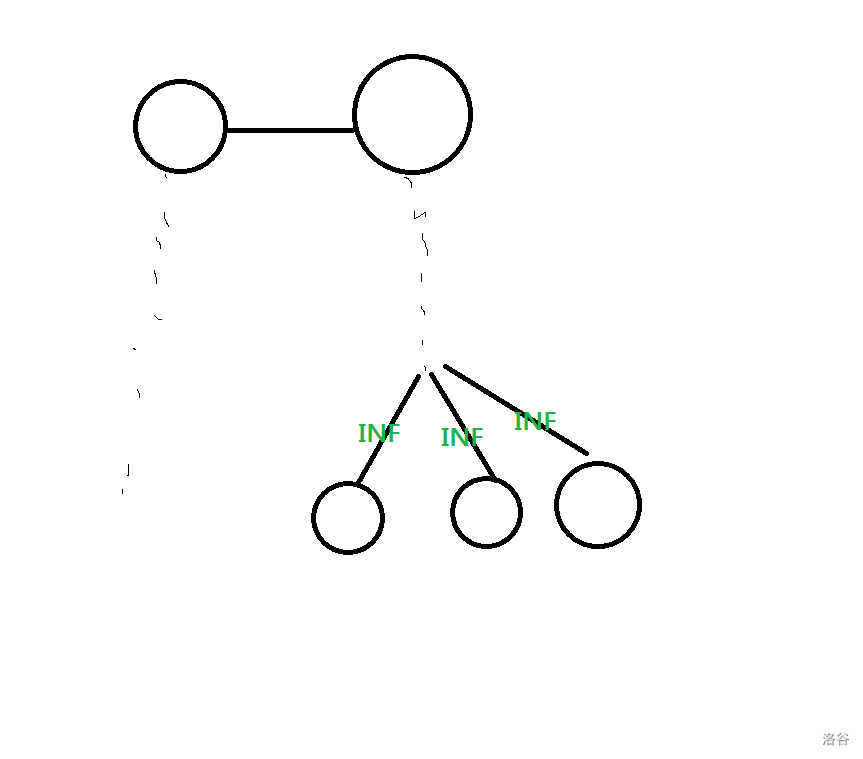
对于后面的点，考虑如下构造：

其中，蓝色的点是已经确定在左边的任意一个点，红色的点是当前要确定的边对应的点。

可以发现，将图中的三条边设置为

\inf

后，若红点在右边，则直径为

3\inf

，否则直径为

2\inf

。

于是可以通过一次询问确定每条边在哪一边，从而确定第一层。

接下来考虑在已知上一层的情况下构造下一层。

问题在于如何求出来每条边接在哪个点下边。

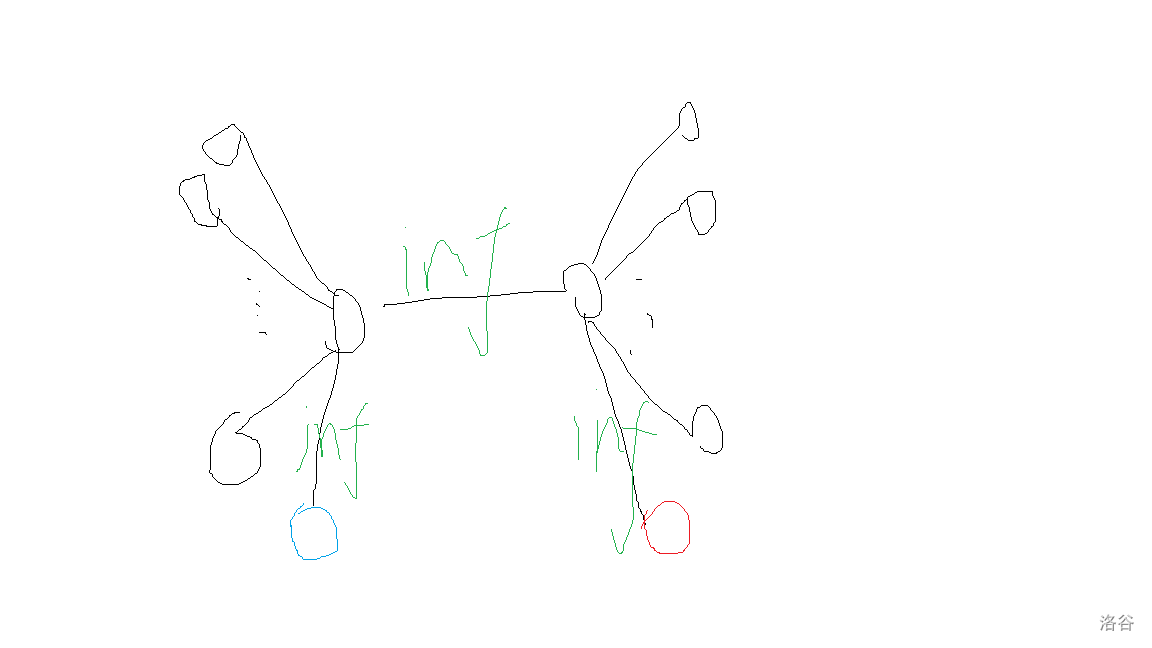
考虑如下构造：

也就是给上一层的每个点和父亲的连边设置为

k\inf

，其中

k

表示这个点的编号。

定义 INF 为比

\inf

大一个数量级的极大值，考虑把要查询的边权设置为 INF，则直径一定形如下图蓝色路径

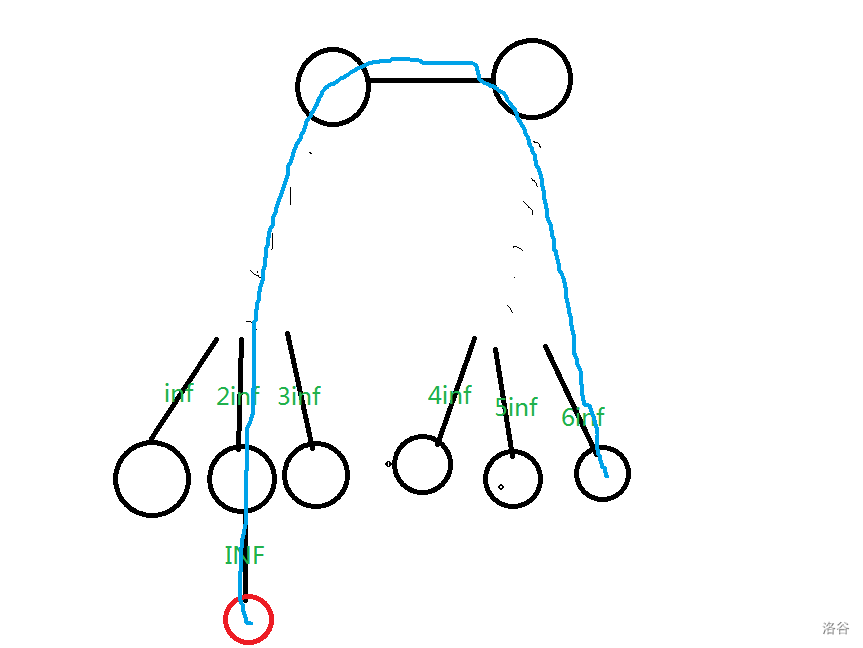
也就是我们用求出来的直径减去 INF，再减去

k\inf

中最大的那个，得到的结果除以

\inf

就是这条边连到的点的编号。

但是会有一种特殊情况：当前的边连到的点是编号最大的点。

此时，直径会经过编号最大和次大的点。

也就是，用上述方法得到的编号若不是编号次大的点，则可以确定。

否则，这条边连到的点可能是最大和次大的点之一。

考虑如何确定这条边具体连到哪个点。

若编号最大和次大的点同时在右边，则可以考虑如下构造：

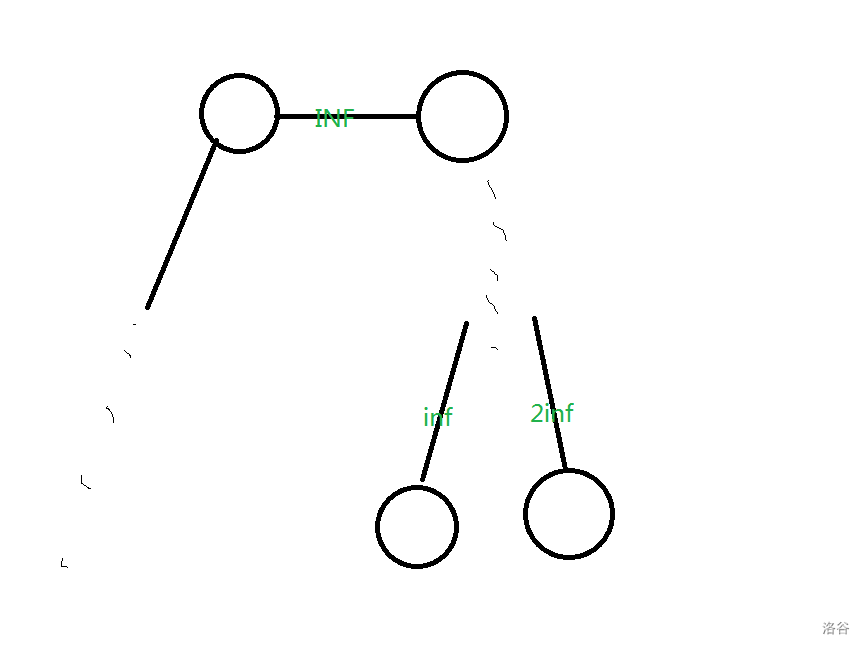
把要确定的边的边权设置为 INF，让直径减去

2

个 INF，看得到的结果是

\inf

还是

2\inf

，就能确定接在哪个点上。

若编号最大和次大的点分别在两边，则可以先找到一个已经确定的点，使得这个点不是这两个点中任何一个点的祖先，把这个点和父亲的连边设为 INF，最大和次大的点和父亲的连边同上，要确定的边设为 INF，就可以用同上的方法确定。

如果找不到这么一个点，则整棵树一定由两条对称的链构成。此时可以发现，把这条边接在哪里都是一样的，所以随便选一个即可。

通过上述构造，每条边加入时最多需要

2

次询问，我们得到了一个最多需要

2n

次第一类询问，

n-2

次第二类询问的做法。

考虑继续优化，能否一次询问确定一条边？

延续上面的思路，如果我们能找到一个已经确定为叶子的点，则可以进行下图的构造：

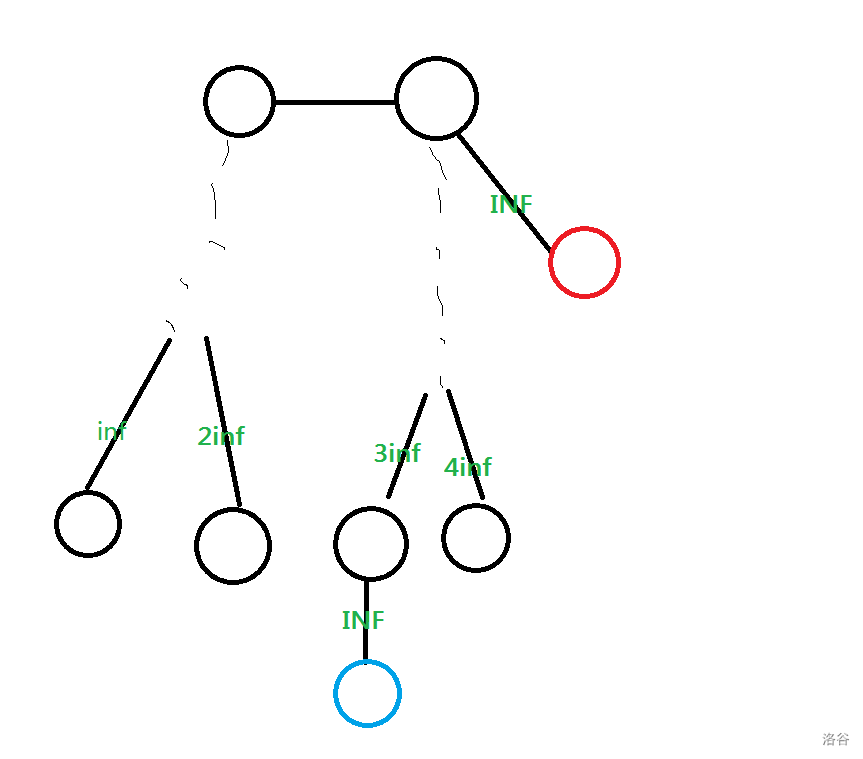
套用上文的做法，可以发现由于红点下方一定不再接其它点，所以这种构造下不再会产生冲突，也就是可以通过

1

次询问确定。

但是可能不存在这样的点。

假如我们已经确定了这一层的第一个点，则可以将这个确定的点作为上图的红点，但是不同的地方是当红点和蓝点接到同一个点上时，求出的直径减去两个 INF 后为

0

。

现在，问题在于如何确定每一层的第一个点。

考虑能否通过两次操作同时问出来两个点。

考虑如下构造：

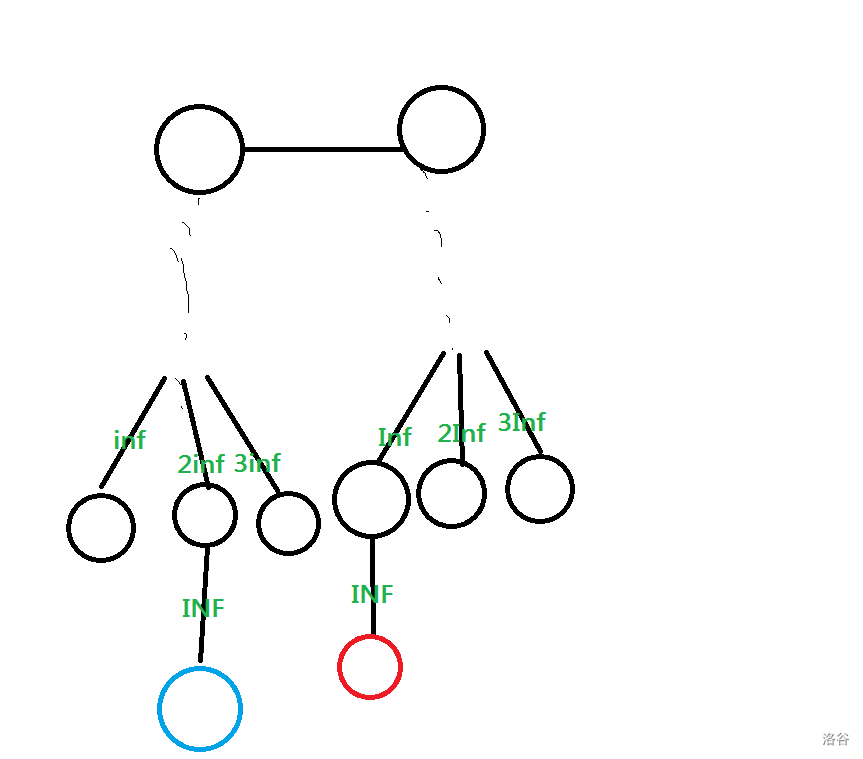
其中，Inf 是数量级介于

\inf

和 INF 之间的极大值。

我们想同时确定红点和蓝点相连的边。

可以发现，存在以下四种情况：

红点和蓝点都在左侧。

此时，我们知道红点和蓝点的编号和，只需要将根设为 INF，蓝点设为 INF，不考虑红点，只保留上一层在左侧的点和父亲的连边，则可以求出蓝点连在哪个点下面，然后作差得到红点连接的点的编号。

红点和蓝点都在右侧。

同第一种情况。

红点和蓝点分别在两侧。

此时，由于我们设置了两个不同数量级的极大值，所以可以直接求出来两个点连接的两个点的编号，但是不知道对应关系。

只需要知道红点和蓝点哪个在左侧，哪个在右侧即可，也就是要判断红点是否在左侧。考虑如下构造：

如果红点在左侧，则直径为 INF，否则直径为两倍 INF。

但是还会有右侧只有一个点的情况，此时可以把判断放到左侧。如果两侧都只有一个点，则整棵树一定由两条相同的链构成。否则就说明这棵树至少有一个已经确定为叶子的节点，则会在上文中被解决。此时，接在哪里都是无所谓的。

红点和蓝点接在同一个点上。

此时，可以把这两个点合并，放到后面一起确定。

还有最后一种情况就是这一层所有点都接在同一个点上。

此时直接套用上文的

2

步的解法。由于这种情况出现后，一定会产生至少一个叶子，所以这种情况只会出现一次。

综上，我们用不超过

n

次第一类操作解决了这个问题。

最后还需要注意一个点：由于我们用到了

3

个数量级，所以

10^9

可能不够用，需要动态调整

\inf

值。

CPP

#include <bits/stdc++.h>
#define int long long
using namespace std;
int ask1(vector<signed>q){
	cout<<"? 1 ";
	for(auto c:q)cout<<c<<" ";
	cout<<endl;
	int x;
	cin>>x;
	return x;
}
int ask2(int a,int b){
	cout<<"? 2 "<<a+1<<" "<<b+1<<endl;
	int x;
	cin>>x;
	return x;
}
const int N=1e3+5,T=1000,G=1e6,B=1e9;
int dep[N],idx=2,dy[N],fa[N],bk[N],bh[N],ok[N];
vector<pair<signed,signed> >rs;
vector<int>q,jl;
vector<pair<signed,signed> >solve(signed t,signed n,signed lim1,signed lim2){
    vector<signed>g;
    auto sets=[&](int x,int y){
    	g[x-1]=y;
    };
    auto upt=[&](int x){
    	while(x){
    		bk[x]=1;
    		x=fa[x];
    	}
    };
	auto init=[&](){
		for(int i=0;i<n-1;i++)g[i]=1;
	};
	for(int i=2;i<n;i++)dep[i]=ask2(0,i-1);
	int tmp=0;
	bh[1]=1;bh[2]=2;
	g.resize(n-1);
	rs.push_back({1,2});
	for(int i=2;i<n;i++){
		if(dep[i]==0){
			if(!tmp){
				idx++;
				rs.push_back({2,idx});
				fa[idx]=2;
				bh[idx]=2;
				dy[i]=idx;
				tmp=i;
			}else{
				init();
				sets(1,T);
				sets(tmp,T);
				sets(i,T);
				int sm=ask1(g);
				idx++;
				dy[i]=idx;
				if(sm>=3*T){
					rs.push_back({1,idx});
					fa[idx]=1;
					bh[idx]=1;
				}else{
					rs.push_back({2,idx});
					fa[idx]=2;
					bh[idx]=2;
				}
			}
		}
	}
	for(int i=1;i<=n;i++){
	    auto add=[&](int a,int b){
			idx++;
			dy[a]=idx;
			fa[idx]=b;
			bh[idx]=bh[b];
			rs.push_back({b,idx});
		};
	    auto Solve=[&](int j){
			init();
			for(int k=1;k<=jl.size();k++)sets(jl[k-1],k*T);
			sets(j,B);
			int sm=ask1(g);
			sm-=B;
			sm/=T;
			int a=jl.back(),b=jl[sm-jl.size()-1];
			if(sm-jl.size()!=jl.size()-1){
				idx++;
				rs.push_back({dy[b],idx});
				fa[idx]=dy[b];
				bh[idx]=bh[dy[b]];
				dy[j]=idx;
				return;
			}
			if(bh[dy[a]]==bh[dy[b]]){
				init();
				sets(j,B);
				sets(a,T);
				sets(b,2*T);
				sets(1,B);
				int sm=ask1(g);
				sm-=2*B;
				idx++;
				if(sm>=2*T){
					rs.push_back({dy[b],idx});
					fa[idx]=dy[b];
					bh[idx]=bh[dy[b]];
					dy[j]=idx;
				}else{
					rs.push_back({dy[a],idx});
					fa[idx]=dy[a];
					bh[idx]=bh[dy[a]];
					dy[j]=idx;
				}
				return;
			}
			memset(bk,0,sizeof(bk));
			upt(dy[a]);upt(dy[b]);
			int wz=0;
			for(int k=2;k<n;k++){
				if(dep[k]>=i)continue;
				if(!bk[dy[k]]){
					wz=k;
					break;
				}
			}
			if(!wz){
				idx++;
				rs.push_back({dy[a],idx});
				fa[idx]=dy[a];
				bh[idx]=bh[dy[a]];
				dy[j]=idx;
				return;
			}else{
				init();
				sets(wz,B);
				sets(1,B);
				sets(j,B);
				int sm=ask1(g);
				if(sm>=3*B){
					if(bh[dy[wz]]!=bh[dy[a]]){
						idx++;
						rs.push_back({dy[a],idx});
						fa[idx]=dy[a];
						bh[idx]=bh[dy[a]];
						dy[j]=idx;
					}else{
						idx++;
						rs.push_back({dy[b],idx});
						fa[idx]=dy[b];
						bh[idx]=bh[dy[b]];
						dy[j]=idx;
					}
				}else{
					if(bh[dy[wz]]==bh[dy[a]]){
						idx++;
						rs.push_back({dy[a],idx});
						fa[idx]=dy[a];
						bh[idx]=bh[dy[a]];
						dy[j]=idx;
					}else{
						idx++;
						rs.push_back({dy[b],idx});
						fa[idx]=dy[b];
						bh[idx]=bh[dy[b]];
						dy[j]=idx;
					}
				}
			}
		};
		auto pd=[&](int j){
		  	init();
		  	sets(j,B);
		  	int sm1=0,sm2=0;
		  	for(int k=1;k<=jl.size();k++){
		  		if(bh[dy[jl[k-1]]]==1)sm1++;
		  		else sm2++;
		  	}
		  	if(sm1>1){
		  		for(int k=1;k<=jl.size();k++){
		  			if(bh[dy[jl[k-1]]]==1)sets(jl[k-1],T);
		  		}
		  		return ask1(g)-B>=2*T;
		  	}else if(sm2>1){
		  		for(int k=1;k<=jl.size();k++){
		  			if(bh[dy[jl[k-1]]]==2)sets(jl[k-1],T);
		  		}
		  		return ask1(g)-B<2*T;
		  	}else return true;
		};
	    memset(ok,0,sizeof(ok));
		for(int j=3;j<=idx;j++)ok[fa[j]]=1;
		int ww=0;
		for(int j=2;j<n;j++){
			if(dep[j]>=i-1)continue;
			if(ok[dy[j]])continue;
			ww=j;
		}
		jl.clear();
		for(int j=2;j<n;j++){
			if(dep[j]==i-1){
				jl.push_back(j);
			}
		}
		if(!jl.size())break;
		if(jl.size()==1){
			for(int j=2;j<n;j++){
				if(dep[j]==i){
					idx++;
					rs.push_back({dy[jl[0]],idx});
					fa[idx]=dy[jl[0]];
					bh[idx]=bh[fa[idx]];
					dy[j]=idx;
				}
			}
			continue;
		}
		random_shuffle(jl.begin(),jl.end());
		int tmp=0;
		vector<int>lj;
		for(int j=2;j<n;j++){
			if(dep[j]==i){
				if(!tmp){
			//		cout<<"d"<<j<<" "<<ww<<endl;
					if(ww){
					    tmp=j;
					    init();
					    for(int k=1;k<=jl.size();k++){
					    	sets(jl[k-1],k*T);
					   // 	cout<<k<<" "<<jl[k-1]<<" "<<dy[jl[k-1]]<<endl;
					    }
					    sets(j,B);
						sets(ww,B);
						int sm=ask1(g);
						sm-=2*B;
						sm/=T;
						int b=jl[sm-1];
					//	cerr<<sm<<"--"<<b<<endl;
						idx++;
						rs.push_back({dy[b],idx});
						fa[idx]=dy[b];
						bh[idx]=bh[dy[b]];
						dy[j]=idx;
						continue;
					}
					if(!lj.size()){
						lj.push_back(j);
						continue;
					}
					init();
					int T=n-jl.size(),G=2*T*jl.size();
					for(int k=1;k<=jl.size();k++){
						if(bh[dy[jl[k-1]]]==1)sets(jl[k-1],k*T);
						else sets(jl[k-1],k*G);
					}
					int lst=lj[0];
					sets(j,B);
					sets(lst,B);
					int sm=ask1(g);
					sm-=2*B;
					if(sm<T){
						lj.push_back(j);
						continue;
					}else if(sm<G){
						sm/=T;
						init();
						for(int k=1;k<=jl.size();k++){
							if(bh[dy[jl[k-1]]]==1)sets(jl[k-1],k*T);
						}
						sets(j,B);
						sets(1,B);
						int sms=ask1(g);
						sms-=2*B;
						sms/=T;
						int to1=dy[jl[sms-1]],to2=dy[jl[sm-sms-1]];
						add(j,to1);
						for(auto c:lj){
							add(c,to2);
						}
						lj.clear();
					}else if(sm%G<T){
						sm/=G;
						init();
						for(int k=1;k<=jl.size();k++){
							if(bh[dy[jl[k-1]]]==2)sets(jl[k-1],k*T);
						}
						sets(j,B);
						sets(1,B);
						int sms=ask1(g);
						sms-=2*B;
						sms/=T;
						int to1=dy[jl[sms-1]],to2=dy[jl[sm-sms-1]];
						add(j,to1);
						for(auto c:lj)add(c,to2);
						lj.clear();
					}else{
						int s1=sm%G/T,s2=sm/G,to1=dy[jl[s1-1]],to2=dy[jl[s2-1]];
					//	cerr<<to1<<"--"<<to2<<endl;
						if(pd(j)){
							add(j,to1);
							for(auto c:lj)add(c,to2);
						}else{
							add(j,to2);
							for(auto c:lj)add(c,to1);
						}
						lj.clear();
					}
					tmp=j;
				}else{
					init();
					sets(tmp,B);
					sets(j,B);
					int tt=0;
					for(int k=1;k<=jl.size();k++){
						sets(jl[k-1],k*T);
						if(dy[jl[k-1]]==fa[dy[tmp]])tt=k;
					}
					int sm=ask1(g),to;
					sm-=2*B;
					sm/=T;
					if(!sm){
						to=fa[dy[tmp]];
					}else{
						sm-=tt;
						to=dy[jl[sm-1]];
					}
					idx++;
					rs.push_back({to,idx});
					fa[idx]=to;
					dy[j]=idx;
					bh[idx]=bh[to];
				}
			}
		}
		if(lj.size()){
			Solve(lj[0]);
			int tmp=fa[dy[lj[0]]];
			for(int j=1;j<lj.size();j++)add(lj[j],tmp);
		}
	}
	//for(auto [a,b]:rs)cerr<<a<<"-"<<b<<endl;
	return rs;
}
signed main(){
	int n;
	cin>>n;
	auto rs=solve(0,n,0,0);
	cout<<"!"<<endl;
	for(auto [a,b]:rs)cout<<a<<" "<<b<<"\n";
}

文章操作

相关推荐

评论

Tree Diameter