题解：P12369 [蓝桥杯 2022 省 Python B] 全排列的价值

P12369 [蓝桥杯 2022 省 Python B] 全排列的价值题解

分享一种不用逆元的做法。

考虑线性递推。设答案为

f(n)

，那么对于前面已知的

f(n-1)

，设它的一种全排列方式为

a_1,a_2,a_3,\cdots,a_{n-1}

。

如图，将

n

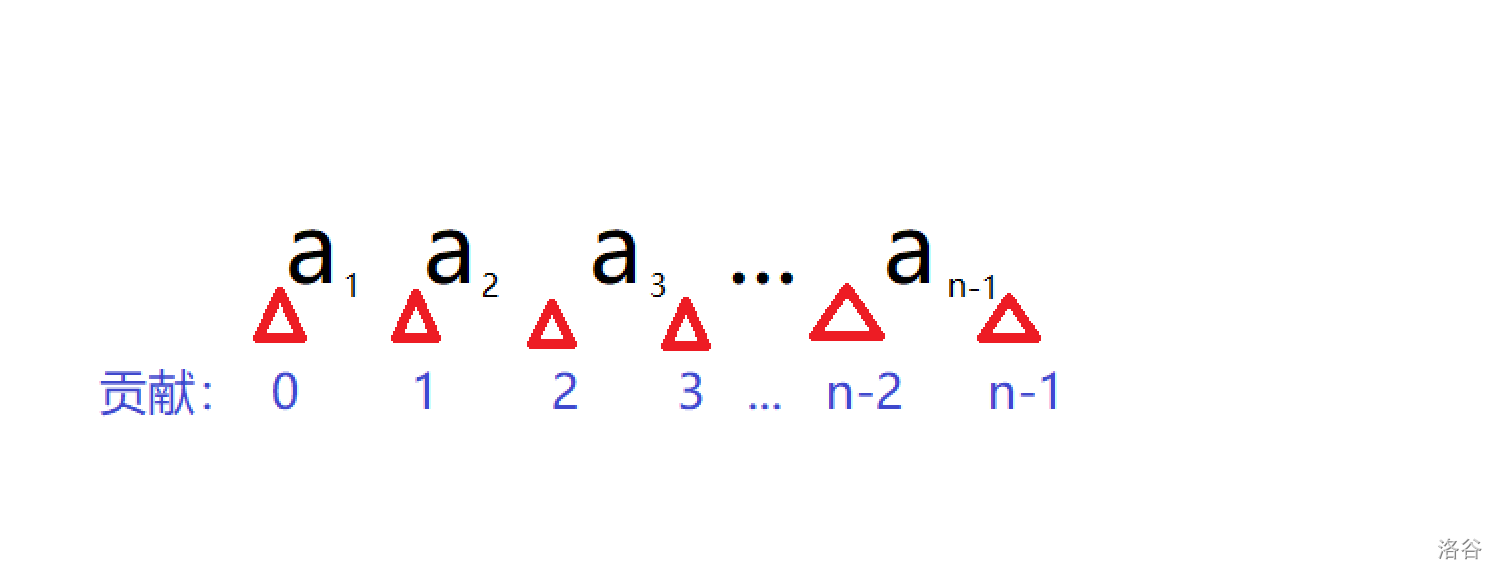
的增加视为向这个排列内插入一个

n

，算上该序列的头尾，共有

n

个位置可以插，插在第

k

个位置上的贡献即为该位置前方元素的数量，即

k-1

（因为这时

n

一定是最大的，前面的所有元素都比它小，后面的所有元素都没它大，所以只对前面有影响）。因此该排列下插入带来的贡献为：

\sum^n_{k=1}k-1=\dfrac{n(n-1)}{2}

~~（挺显然的说是…）~~

每次不同的插入方法都视为一种答案，

n

种方法，就需要将原答案数乘

n

。在

n-1

下的

(n-1)!

个排列都得计算一遍，合起来就是总答案的

n

倍与插入带来的总贡献

\dfrac{n(n-1)}{2}(n-1)!

之和。初始的状态为

n=2

，答案显然为

1

。于是我们即可得到递推式：

1 & n=2\\ nf(n-1)+\dfrac{n(n-1)}{2}(n-1)! & n>2 \end{cases}$$ 时间复杂度 $O(n)$。阶乘采用预处理。 ### C++ ```cpp #include<bits/stdc++.h> #define ll long long using namespace std; const ll N=1e6+5,mod=998244353; ll n,ans[N],jc[N]={1,1}; int main() { cin>>n; ans[2]=1; for(int i=1; i<=N; i++) jc[i]=jc[i-1]*i%mod;//阶乘预处理 for(int i=3; i<=n; i++) ans[i]=(i*1ll*ans[i-1]%mod+i*1ll*(i-1)/2ll%mod*1ll*jc[i-1]%mod)%mod; //记住在常数后面加 ll 防止转 int 炸掉 //由于 i*(i-1) 一定为偶数，所以可以直接 /2 而不用考虑逆元 cout<<ans[n]%mod; return 0; } ``` ### Python ```python mod = 998244353 N = 1000005 n = int(input()) ans = [0] * N ans[2] = 1 jc = [1] * N for i in range(1, N): jc[i] = (jc[i-1] * i) % mod for i in range(3, n + 1): t1 = (i * ans[i-1]) % mod t2 = ((i * (i - 1) // 2) % mod) * jc[i-1] % mod ans[i] = (t1 + t2) % mod print(ans[n] % mod) ``` upd on 2025/5/5 18:30：添加了 Python 代码。 upd on 2025/6/7 22:05：修改了凌乱冗余的语言描述，增强可读性。