P3207 [HNOI2010] 物品调度

题意

题面有点令人犯恶心，先理清楚：

首先有个需要你生成的数组

c

，生成所需变量是用题目给你的：

p

、

q

和

m

。

生成规则是：

c_0=0

，

c_{i+1}=(c_i \times q + p)

mod

m

。

每个盒子还有一个最终位置为

pos_i

，

pos_i=(c_i+d \times x_i+y_i)

mod

n

。注意，这个

x_i

和

y_i

你是不知道的，要你自己生成。满足首先

y

的字典序要最小，其次是

x

的字典序也要小。

每次移动可以将某一个盒子移到空位上，问把所有的盒子移动到最终位置所需的最少步数。

解法

其实比较容易可以发现，增加

x

会使得整个序列在操作的时候变成一个环，环与环之间的关系又要由

y

来决定。此时就可以使用并查集进行优化，把使用了的位置连向空位。

求答案的时候就需要判断一下这个置换环内有没有空格，如果有空格就是环内元素个数减

1

，否则加

1

。什么意思呢？如下图：

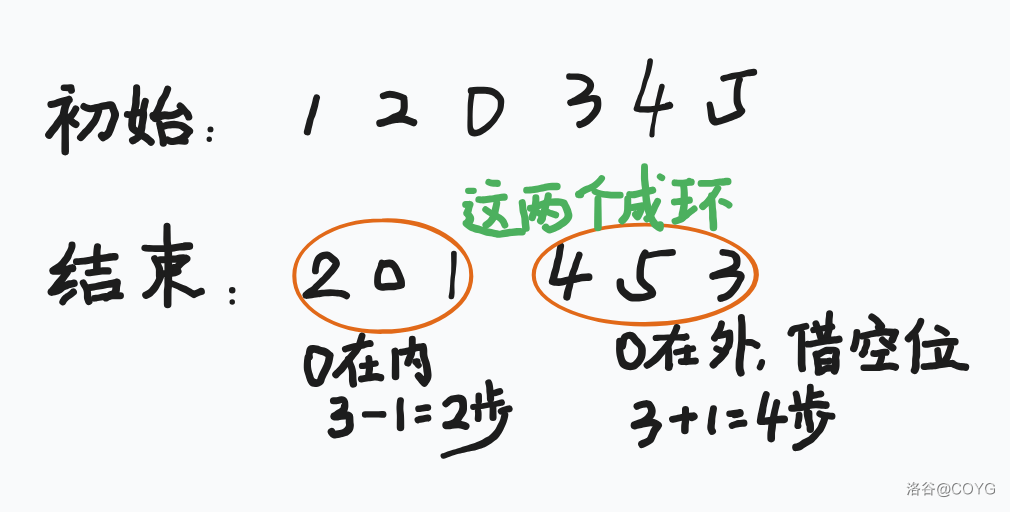
注意的点

有一些小细节可以根据代码理解。

code

CPP

#include<bits/stdc++.h>
#define int long long
#define N 100005
using namespace std;
bool vis[N];
int T,n,s,p,q,m,d,ans,a[N],c[N],fa[N],pos[N];
int find(int x){return fa[x]==x?x:(fa[x]=find(fa[x]));}
signed main(){
    scanf("%lld",&T);
    while(T--){
        scanf("%lld%lld%lld%lld%lld%lld",&n,&s,&p,&q,&m,&d);
        for(int i=0;i<n;i++) a[i]=0,fa[i]=i,vis[i]=0;
        vis[pos[0]=s]=1,ans=c[0]=0,fa[s]=(s+d)%n;
        for(int i=1;i<n;i++) c[i]=(c[i-1]*p+q)%m;
        for(int i=1;i<n;i++){
            int y=0;
            while(vis[find((y+c[i])%n)]) y++;
            pos[i]=find((y+c[i])%n);
            vis[pos[i]]=1,fa[pos[i]]=find((pos[i]+d)%n);
        }
        for(int i=0;i<n;i++) if(!a[i]&&pos[i]!=i){
            bool pd=0;
			int p=i,cnt=0;
			while(!a[p]){
				if(!p) pd=1;
                a[p]=1,p=pos[p],cnt++;
			}
            ans+=cnt+(pd?-1:1);
        }
        printf("%lld\n",ans);
    }
    return 0;
}

题解：P3207 [HNOI2010] 物品调度

文章操作

P3207 [HNOI2010] 物品调度

题意

解法

注意的点

code

相关推荐

评论

题解：P3207 [HNOI2010] 物品调度