题解：P14211 [ROI 2016 Day2] 快递服务

STOOOOOOOOOOOO cyx CCCCCCCCCCCCOTZ。

首先考虑所有路径都是从 $1$ 开始的一条链怎么做。根据经典结论，交集最大的一定另一个端点按照 dfn 排序后相邻的两条链或者是最靠前和最靠后的两条链。直接求 LCA 计算即可。

考虑拓展。先将两条路径 LCA 不同的情况的答案求出来，可以将路径拆为 $lca\rightarrow x$ 和 $lca\rightarrow y$ 两种。用树形 dp 对每个子树求出可以连向该子树中任意一个点的 $lca$ 中深度最小的和次小的，答案就是该子树根节点的深度减去次小的深度。

然后考虑 LCA 相同的情况，此时形态如下图所示：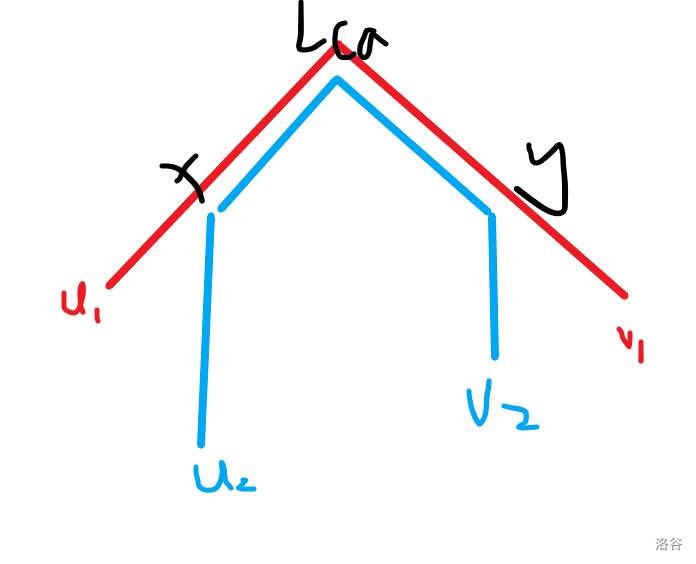

考虑枚举 $x$，此时的答案为 $dep_x+dep_y-2\times dep_{lca}=dep_x+dep_{\operatorname{lca}(v_2,v_1)}-2\times dep_{u_1,v_1}$。这启发我们维护该子树内的路径端点，并在合并两个子树时统计答案。利用启发式合并维护出子树内端点集合，每次插入一个端点前先更新答案。根据前面路径全都为 $1$ 开始的一条链的做法，我们在 set 中按照 dfn 排序，每次查询二分找到当前插入点的前驱和后继更新答案即可。

这个时候还有一个问题。对于一条链，如果其两个端点都在当前的子树内显然不应该将其统计进答案，所以需要对于每个路径在 LCA 处将其删去。

最终时间复杂度 $\operatorname{O}(n\log^2n)$，可以通过，细节比较多，可以看代码。