专栏文章

树状数组

xxhraiganf
算法·理论参与者 3已保存评论 2

文章操作

快速查看文章及其快照的属性，并进行相关操作。

当前评论
2 条
当前快照
1 份
快照标识符
@mlmknykc
此快照首次捕获于
2026/02/15 01:10
5 天前
此快照最后确认于
2026/02/19 01:12
14 小时前
查看原文

原理

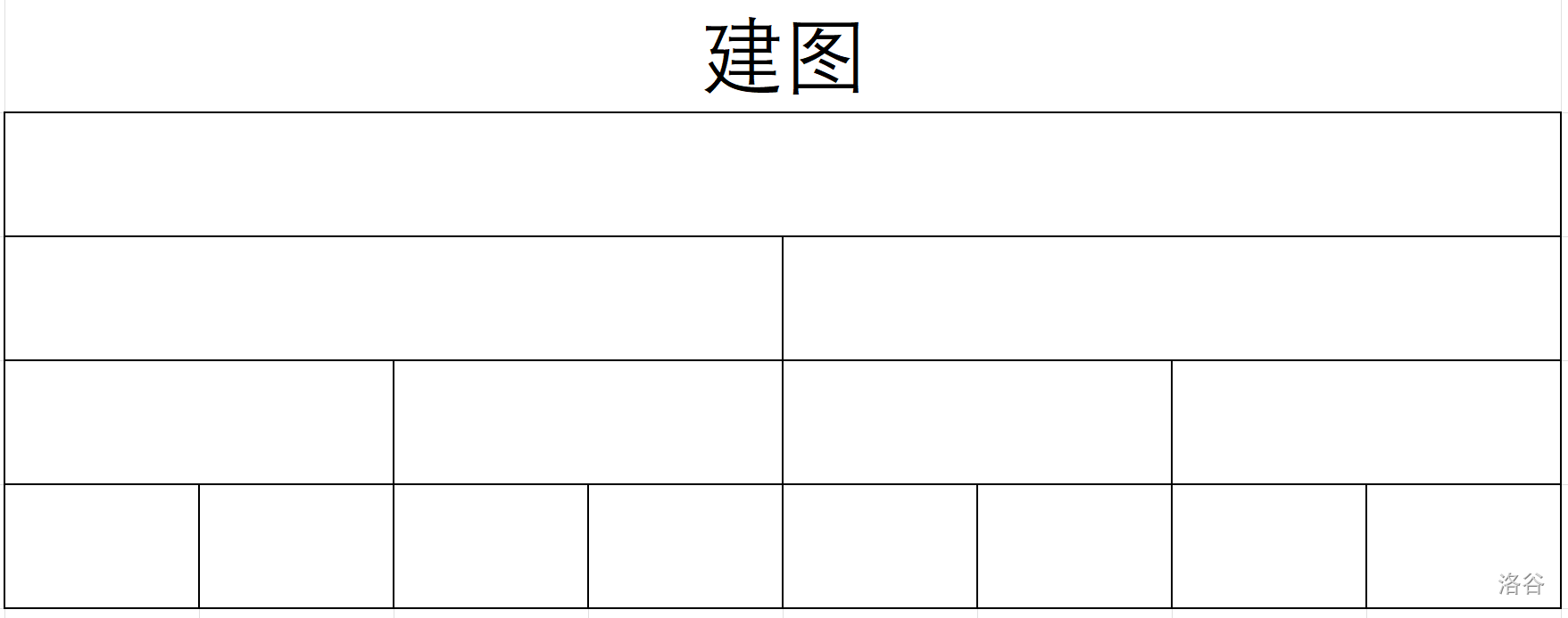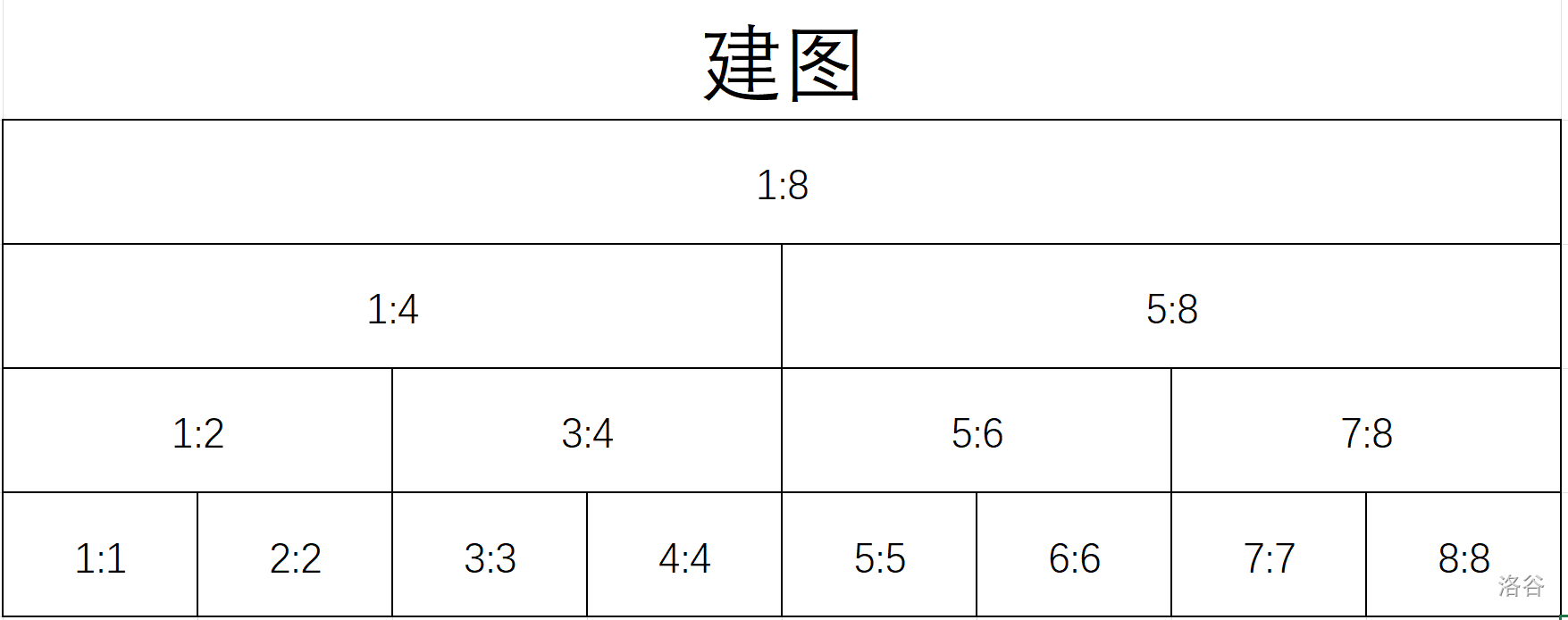
先看下面这图: 填上数值: xx,y的区间和
这样我们可以求任意区间的区间和
例: [2:7]=[2:2]+[3:4]+[5:6]+[7:7][2:7]=[2:2]+[3:4]+[5:6]+[7:7]
但这样会有冗余, 于是我们把每一行的偶数位删除: 于是删除的位数都可以用减法得到
然后让剩下的每一个区间对应上一个数组的值:
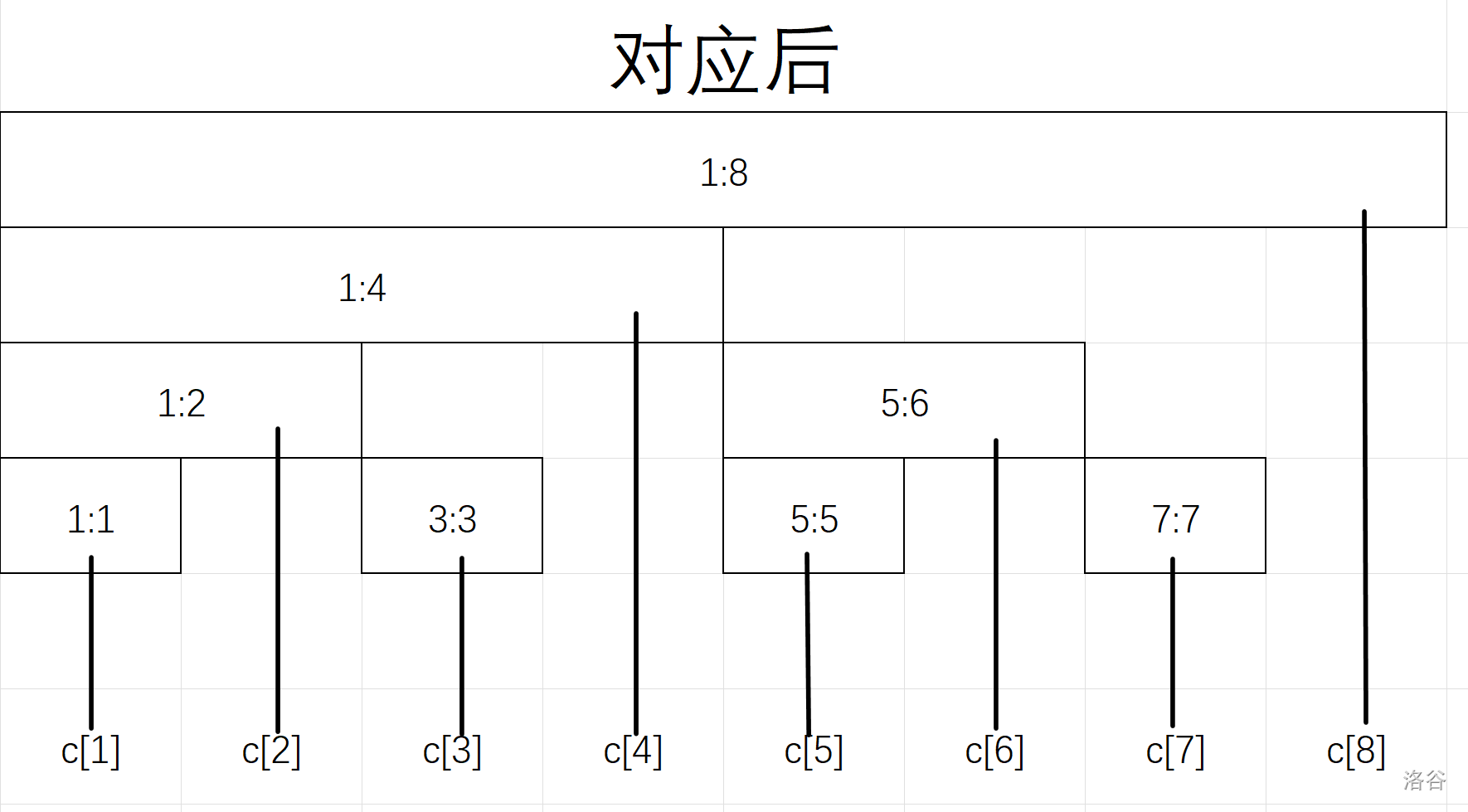
我们发现:
c[i]c[i]对应的长度是 ii 转二进制后的最末尾的 1 和其后面的 0 组成的数值, 记作lowbit(i)lowbit(i)
例: c[6]c[6]：它的二进制是(110)2(110)_2,所以lowbit(6)=10lowbit(6)=10也就对应着它的区间长度22
lowbit的实现
将xx的二进制全部取反+1+1记为yy,再将xx & yy，就可以得到最后一位 11 的位置
详细请看: https://www.cnblogs.com/fusiwei/p/11752540.html
code:
CPP
int lowbit(int x) {
  return (x & (-x));
}

区间查询

根据前缀和的定义，每一个区间和[l,r][l,r]都可以由[1,r]−[1,l−1][1,r]-[1,l-1]得来
这样求一个区间就被拆分成两个小过程
然后我们看一些例子(根据图四):
  1. [1:7][1:7]可以分为:[1:4]+[5:6]+[7:7]=c[4]+c[6]+c[7][1:4]+[5:6]+[7:7]=c[4]+c[6]+c[7]
  2. [1:5][1:5]可以分为:[1:4]+[5:5]=c[4]+c[5][1:4]+[5:5]=c[4]+c[5]
看1号例子: c[6]c[6] 的 66 是由后面的 c[7]c[7] 的 7−lowbit(7)7-lowbit(7) 得来的, c[4]c[4] 的 44 是由后面的 c[6]c[6] 的 6−lowbit(6)6-lowbit(6) 得来的
结论:
前一个数的值=后一个数的值−lowbit(后一个数的值)前一个数的值=后一个数的值-lowbit(后一个数的值)
所以,我们就可以从当前xx不停往前加,求出[1:x][1:x]的值
再用前缀和求出当前区间的值
code:
CPP
int query(int x){
	int ans=0;
	while(x>0){
		ans+=c[x];
		x-=lowbit(x);
	}
	return ans;
}
query(r)-query(l-1)//[l:r]的区间值

单点修改

因为每一个区间都是由一个它包含的子区间的和得来
若我们修改一个点的值，那么它所对应的区间的和要改，包含这个区间的区间和也要修改，包含包含这个区间的区间的区间和也要修改(禁止套娃)
例子(根据图四):
修改33号点的值，那么[3:3]、[1:4]、[1:8][3:3]、[1:4]、[1:8]也需修改，也就是:c[3]c[3]、c[4]c[4]、c[8]c[8]
观察一下: c[4]c[4] 的 44 是由 3+lowbit(3)3+lowbit(3) 得来, c[8]c[8] 的 88 是由 4+lowbit(4)4+lowbit(4) 得来
结论:
后一个数的值=前一个数的值+lowbit(前一个数的值)后一个数的值=前一个数的值+lowbit(前一个数的值)
但: 值最大取到 nn，所以循环边界就是 nn
code:
CPP
void modify(int x,int v){
	while(x<=n){
		c[x]+=v;
		x+=lowbit(x);
	}
}

区间修改

这里需用到差分
差分
详细请见: https://oi-wiki.org/basic/prefix-sum/
是前缀和的逆运算，先需求差分数组(disdis)
dis[i]=a[i]−a[i−1]dis[i]=a[i]-a[i-1]
修改区间[l,r][l,r]，就是让
dis[l]+xdis[l]+x，dis[r+1]−xdis[r+1]-x
再求一遍前缀和得到修改过后的原数组
但这样修改虽是O(1)O(1)的，但查询却是O(n)O(n)的，是一种适用于大量修改、少量查询的算法
我们让树状数组维护这个差分的过程,每次让[1,l][1,l]加上xx,让[1,r+1][1,r+1]减去xx,于是我们就记录下了区间[l,r]+x[l,r]+x的值
code:
CPP
void update(int x,int v){
    while(x<=n){
        c[x]+=v;
        x+=lowbit(x);
    }
}
update(l,x);
update(r+1,-x);

单点查询

根据区间修改，我们得知了每个区间的被修改的值
于是我们只需求出包含当前点的区间总和+当前点原来的数值
code:
CPP
int query(int x){
    int ans=0;
    while(x>0){
        ans+=c[x];
        x-=lowbit(x);
    }
    return ans;
}
a[x]+query(x)

例题

T1.U438237 ١١(❛ᴗ❛)【树状数组+线段树】-模板（单点修改+区间查询）

这一题模板题,直接套不多讲
code:
CPP
#include<bits/stdc++.h>
using namespace std;
#define int long long
int c[1000010];
int n,q;
int lowbit(int x){
	return (x&(-x));
}
int query(int x){
	int ans=0;
	while(x>0){
		ans+=c[x];
		x-=lowbit(x);
	}
	return ans;
}
void update(int x,int v){
	while(x<=n){
		c[x]+=v;
		x+=lowbit(x);
	}
}
signed main(){
	cin>>n>>q;
	for(int v,i=1;i<=n;i++){
		cin>>v;
		update(i,v); 
	} 
	for(int i=1;i<=q;i++){
		int op,l,r;
		cin>>op>>l>>r;
		if(op==1){
			update(l,r);//单点修改
		}else{
			cout<<query(r)-query(l-1)<<endl;//区间查询求前缀和
		}
	}
	return 0;
}

T2.U438249 清点人数

这一题与上题板子的区别有:
  • 这一题区间查询只需求[1,m][1,m]的区间和
  • 有加有减
code:
CPP
#include<bits/stdc++.h>
using namespace std;
#define int long long
int c[1000010];
int n,k;
int lowbit(int x){
	return (x&(-x));
}
int query(int x){
	int ans=0;
	while(x>0){
		ans+=c[x];
		x-=lowbit(x);
	}
	return ans;
}
void update(int x,int v){
	while(x<=n){
		c[x]+=v;
		x+=lowbit(x);
	}
}
signed main(){
	cin>>n>>k;
	for(int i=1;i<=k;i++){
		char op;
		cin>>op;
		if(op=='A'){
			int m;
			cin>>m;
			cout<<query(m)<<endl;//只需求[1,m]的区间和
		}else if(op=='B'){
			int m,p;
			cin>>m>>p;
			update(m,p);//加就是正数
		}else{
			int m,p;
			cin>>m>>p;
			update(m,-p);//减就是负数
		}
	}
	return 0;
}

T3.P3368 【模板】树状数组 2

此题是区间修改+单点查询的模板，讲解上面有不多讲
code:
CPP
#include<bits/stdc++.h>
using namespace std;
int c[500010],a[500010];
int n,m;
int lowbit(int x){
    return (x&(-x));
}
int query(int x){
    int ans=0;
    while(x>0){
        ans+=c[x];
        x-=lowbit(x);
    }
    return ans;
}
void update(int x,int v){
    while(x<=n){
        c[x]+=v;
        x+=lowbit(x);
    }
}
int main(){
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        cin>>a[i];
    }
    for(int i=1;i<=m;i++){
        int op;
        cin>>op;
        if(op==1){
            int l,r,x;
            cin>>l>>r>>x;
            update(l,x);
            update(r+1,-x);
        }else{
            int x;
            cin>>x;
            cout<<a[x]+query(x)<<"\n";
        }
    }
    return 0;
}

T4.P5057 [CQOI2006] 简单题

这道题也是区间修改+单点查询的题
与上题的区别:
  • 这里是异或
所以每次查询时只需看包含这个点的区间的状态求它们异或和
每次修改也是跟上一样，因为一个二进制数异或上两个一还是它本身没有变
code:
CPP
#include<bits/stdc++.h>
using namespace std;
#define int long long
int c[1000010];
int a[1000010];
int n,m;
int lowbit(int x){
	return (x&(-x));
}
int query(int x){
	int ans=0;
	while(x>0){
		ans^=c[x];
		x-=lowbit(x);
	}
	return ans;
}
void update(int x,int v){
	while(x<=n){
		c[x]^=v;
		x+=lowbit(x);
	}
}
signed main(){
	cin>>n>>m;
	for(int i=1;i<=m;i++){
		int op;
		cin>>op;
		if(op==1){
			int l,r;
			cin>>l>>r;
			update(l,1);
			update(r+1,1);
		}else{
			int x;
			cin>>x;
			cout<<query(x)<<endl;
		}
	}
	return 0;
}

离散化

因下几题需离散化，所以来讲一下
离散化，本质上是一种哈希，它在哈希后依然能保证顺序不变
它适用于数字很大，但只看相对大小的问题
于是我们可以按顺序给它们编号
离散化分两种:
  1. 相同的值有不同的编号(一般按出现顺序编号)
  2. 相同的值是相同的编号
例:
134262
我们先排序
122346
再编号
第1种:
122346
123456
第2种:
122346
122345
所以用代码模拟以上过程即可

T1.U523499 ١١(❛ᴗ❛)【离散化】-并列大小

这道题属于第2种离散化
每一个相同的值都要编号成相同的号码
做法:
  1. 先复制一份原数组
  2. 将复制数组从小到大排序
  3. 将复制数组去重
  4. 二分查找原数组再复制数组中的位置也就是编号，它就是离散化后的值
code:
CPP
#include<bits/stdc++.h>
using namespace std;
int a[100010];
int tmp[100010];
int main(){
    int n;
    cin>>n;
    for(int i=1;i<=n;i++){
        cin>>a[i];
        tmp[i]=a[i];//复制数组
    }
    sort(tmp+1,tmp+1+n);//排序
    int cnt=unique(tmp+1,tmp+1+n)-tmp-1;//去重
    for(int i=1;i<=n;i++){
        a[i]=lower_bound(tmp+1,tmp+1+cnt,a[i])-tmp;//查找位置
    }
    for(int i=1;i<=n;i++){
        cout<<a[i]<<" ";
    }
    return 0;
}

T2.U523492 ١١(❛ᴗ❛)【离散化】-非并列排名

这道题属于第1种离散化
每一个相同的值都要编号成不同的号码
做法:
  1. 拿一个结构体装它的数值和位置
  2. 排序，若值不同按值从大到小排序，若值相同按位置从小到大排序
  3. 将离散化后的数字放回原数组
code:
CPP
#include<bits/stdc++.h>
using namespace std;
struct node{
    int v,id;
};
node a[100010];
int pos[100010];
bool cmp(node x,node y){
    if(x.v!=y.v)return x.v>y.v;//值不同按值从大到小排序
    return x.id<y.id;值相同按位置从小到大排序
}
int main(){
    int n;
    cin>>n;
    for(int i=1;i<=n;i++){
        cin>>a[i].v;//记录值
        a[i].id=i;//记录位置
    }
    sort(a+1,a+1+n,cmp);
    for(int i=1;i<=n;i++){
        pos[a[i].id]=i;//将离散化的数装回去
    }
    for(int i=1;i<=n;i++){
        cout<<pos[i]<<" ";
    }
    return 0;
}

值域树状数组

T5.U438285 ١١(❛ᴗ❛)【树状数组】-数星星 Stars

先看输入，此题x,yx,y是按yy坐标增序给出，yy 坐标相同的按xx坐标增序给出
所以只要在当前点的左边且xi≥xjx_i \ge x_j这样它就可以升上一级
我们让大的数为一个区间，它下面包含许多小于等于它的数
所以当小于等于它的数来了一个后，它的数值也会+1
code:
CPP
#include<bits/stdc++.h>
using namespace std;
int c[32010];
int ans[32010];
struct node{
    int x,y;
}a[32010];
int n;
int lowbit(int x){
    return (x&(-x));
}
int query(int x){
    int sum=0;
    while(x>0){
        sum+=c[x];
        x-=lowbit(x);
    }
    return sum;
}
void update(int x,int v){
    while(x<=32001){//不是枚举到n
        c[x]+=v;
        x+=lowbit(x);
    }
}
int main(){
    cin>>n;
    for(int i=1;i<=n;i++){
        cin>>a[i].x>>a[i].y;
        a[i].x++;//避免从0开始
    }
    for(int i=1;i<=n;i++){
        ans[query(a[i].x)]++;//查询当前星星的等级并计数
        update(a[i].x,1);//将当前星星加入树状数组
    }
    for(int i=0;i<n;i++){
        cout<<ans[i]<<endl;
    }
    return 0;
}

T6.P1908 逆序对

这道题我们注意到，每个数字的值很大且只要比较它们的相对大小，所以要使用离散化
然后这道题看逆序对也就是找i>ji>j且ai<aja_i<a_j的点
所以用值域树状数组来维护.
code:
CPP
#include<bits/stdc++.h>
using namespace std;
int c[500010],a[500010],tmp[500010];
int n,cnt;
int lowbit(int x){
    return (x&(-x));
}
int query(int x){
    int ans=0;
    while(x>0){
        ans+=c[x];
        x-=lowbit(x);
    }
    return ans;
}
void update(int x,int v){
    while(x<500010){
        c[x]+=v;
        x+=lowbit(x);
    }
}
void lsh(){
    sort(tmp+1,tmp+1+n);
    int cnt=unique(tmp+1,tmp+1+n)-tmp-1;
    for(int i=1;i<=n;i++){
        a[i]=lower_bound(tmp+1,tmp+1+cnt,a[i])-tmp;
        a[i]=cnt-a[i]+1;
    }
}
int main(){
    cin>>n;
    for(int i=1;i<=n;i++){
        cin>>a[i];
        tmp[i]=a[i];
    }
    lsh();
    long long ans=0;
    for(int i=1;i<=n;i++){
        ans+=query(a[i]-1);
        update(a[i],1);
    }
    cout<<ans;
    return 0;
}

评论

共 2 条评论，欢迎与作者交流。

正在加载评论...