专栏文章

题解：P2119 [NOIP 2016 普及组] 魔法阵

QQfaiser
P2119题解参与者 2已保存评论 1

文章操作

快速查看文章及其快照的属性，并进行相关操作。

当前评论
1 条
当前快照
1 份
快照标识符
@mipvd8f6
此快照首次捕获于
2025/12/03 18:33
3 个月前
此快照最后确认于
2025/12/03 18:33
3 个月前
查看原文

solution

一道数学推导优化枚举的题。
容易写出暴力枚举，考虑通过缩小枚举范围优化枚举。
知道 Xa<Xb<Xc<XdX_a<X_b<X_c<X_d 且 Xb−Xa=2(Xd−Xc)<(Xc−Xb)÷3X_b-X_a=2(X_d-X_c)<(X_c-X_b) \div 3。
设一个参数 k=Xd−Xck=X_d-X_c，对原式变形得 Xb−Xa=2kX_b-X_a=2k 和 6k<Xc−Xb6k<X_c-X_b，即 Xb=Xa+2kX_b=X_a+2k 和 Xc>Xb+6kX_c>X_b+6k。
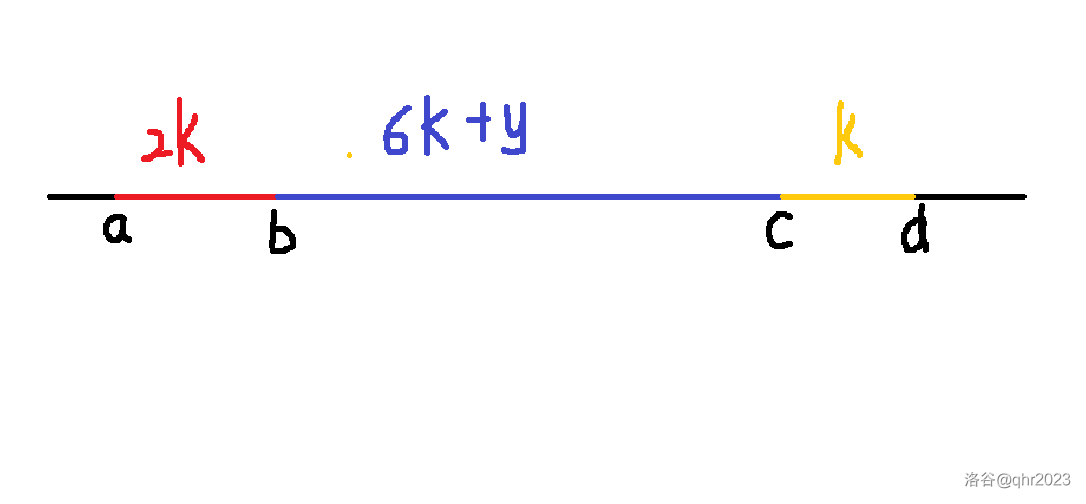
对于每个 kk，XaX_a 到 XbX_b、XcX_c 到 XdX_d 的距离都是定值，而 XbX_b 到 XcX_c 的距离是个区间。
首先要了解这点。若 Xc1<Xc2X_{c_1}<X_{c_2} 且Xd1<Xd2X_{d_1}<X_{d_2}，并且 Xc1−Xb>6kX_{c_1}-X_b > 6k，即 Xc1X_{c_1} 和 Xd1X_{d_1} 可以组成魔法阵，那么 Xc2−Xb>6kX_{c_2}-X_b > 6k，也就是 Xc2X_{c_2} 和 Xd2X_{d_2} 一定可以组成魔法阵。
类似的，若 Xa1<Xa2X_{a_1}<X_{a_2} 且Xb1<Xb2X_{b_1}<X_{b_2}，并且 Xc−Xb2>6kX_c-X_{b_2} > 6k，即 Xa1X_{a_1} 和 Xb1X_{b_1} 可以组成魔法阵，那么 Xc−Xb1>6kX_c-X_{b_1} > 6k，也就是 Xa2X_{a_2} 和 Xb2X_{b_2} 一定可以组成魔法阵。
我们从后往前枚举 XaX_a，记 SxiS_{x_i} 表示 xix_i 出现次数，乘法原理得当前可以作为 XaX_a 的个数为 SXb×SXc×SXdS_{X_b} \times S_{X_c} \times S_{X_d}，用一个后缀和维护 SXc×SXdS_{X_c} \times S_{X_d} 变枚举边算，这样就可以 O(n2)O(n^2) 做了。
从前往后枚举 XdX_d，维护前缀和，同样可以算出贡献。
那就得到了做法，先枚举 kk，再分别枚举 XaX_a 和 XdX_d 的范围计算贡献。
XaX_a 的范围是 11 到 n−9k−yn-9k-y。当 y=1y=1 且 Xd=nX_d=n 时 XaX_a 最大。
XdX_d 的范围是 9k+29k+2 到 nn。当 y=1y=1 且 Xa=1X_a=1 时 XdX_d 最小。
这道题还是有点抽象，不太好描述，可以结合代码体会。

code

CPP
#include <bits/stdc++.h>
using namespace std;
int n, m, A[50005][4], x[50005], num[50005];
int main () {
	cin >> n >> m;
	for (int i=1; i<=m; ++i)
		cin >> x[i],
		num[x[i]]++;
	for (int k=1, a, b, c, d, s; 9*k<=n; ++k) {
		for (a=n-9*k-1, s=0; a>=1; --a) // 枚举a，确定bcd 
			b=a+2*k, c=b+6*k+1, d=c+k,
			s+=num[c]*num[d],
			A[a][0]+=num[b]*s,
			A[b][1]+=num[a]*s;
		for (d=9*k+2, s=0; d<=n; ++d) // 枚举d，确定abc 
			a=d-9*k-1, b=a+2*k, c=d-k,
			s+=num[a]*num[b],
			A[c][2]+=num[d]*s,
			A[d][3]+=num[c]*s;
	}
	for (int i=1; i<=m; ++i, cout << '\n')
		for (int j=0; j<4; ++j)
			cout << A[x[i]][j] << ' ';
	return 0;
}

评论

共 1 条评论，欢迎与作者交流。

正在加载评论...