专栏文章

CF708C Centroids 的题解

AANDER_
CF708C题解参与者 1已保存评论 0

文章操作

快速查看文章及其快照的属性，并进行相关操作。

当前评论
0 条
当前快照
1 份
快照标识符
@mimxbsm4
此快照首次捕获于
2025/12/01 17:05
3 个月前
此快照最后确认于
2025/12/01 17:05
3 个月前
查看原文
好题。
钦定 SuS_u 为点 uu 的子树点集，包含 uu。
钦定 szu=∣Su∣sz_u = |S_u|。
钦定 faufa_u 为 uu 的父亲。
我们以 CF 的 test 4 为例。
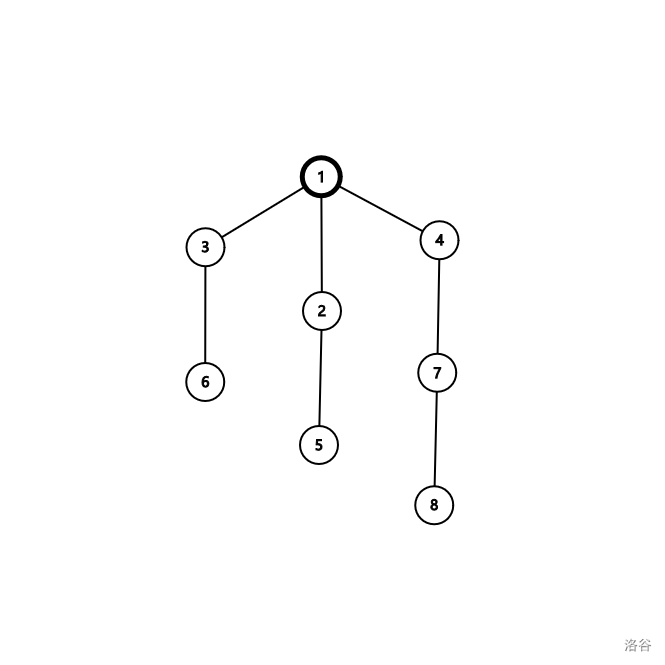
图中的 11 点是重心，关于重心的求法，不再赘述，详见 OI - wiki。
我们可以把根定为重心之一，此图中可以定为 11，这样新树上的每个子树的大小都不超过 ⌊n2⌋\lfloor\frac{n}{2}\rfloor，方便处理。
考虑把重心换到 44 的情况，如何操作，发现联通分量 {1,2,3,5,6}\{1,2,3,5,6\} 大小超过限制。那么显然，我们需要从这个唯一的不合法分量中，拆下一棵子树。并且，最优方案一定是直接将这棵子树直接并到重心 44 上面去，因为这样可以最大限度的避免造出一个新的不合法分量。假设从 SuS_u 中选出子树，令这棵子树的大小为 tt，则需满足：
{t≤⌊n2⌋szu−t≤⌊n2⌋\begin{cases} t &\le \lfloor\frac{n}{2}\rfloor\\ sz_u - t &\le \lfloor\frac{n}{2} \rfloor \end{cases}
因为以原树上的重心为根，则 ∀u∈T,szu≤⌊n2⌋\forall u \isin T,sz_u \le \lfloor\frac{n}{2}\rfloor。因此，只需考虑 T∖SuT \setminus S_u 中的情况。进一步的，我们发现断掉边 e=(u,fau)e = (u, fa_u) 的操作对 uu 是没有意义的，接上去还是一样。因此，设 fuf_u 表示 T∖SuT \setminus S_u 中最大的，大小不超过 ⌊n2⌋\lfloor\frac{n}{2}\rfloor 的连续部分大小。则 fuf_u 可以直接从 ffauf_{fa_u} 继承过来，这是第一种情况。
还有一种情况比较简单，若 ∣T∖SU∣≤⌊n2⌋|T \setminus S_U| \le \lfloor\frac{n}{2} \rfloor，那么 fuf_u 还可以从 n−szun - sz_u 转移过来。
但是，我们还需考虑 uu 的兄弟节点，有可能断掉 uu 的兄弟与 faufa_u 的边。
因为这个情况的研究显然不会再跨过根节点，我们可以直接用子树的大小刻画。
那么设 uu 的兄弟节点集合为 BuB_u，那么 fuf_u 还可以从 max⁡v∈Buszv\displaystyle\max_{v \isin B_u}sz_v 转移过来。为了方便转移，设 uu 的子节点集合为 SonuSon_u，则 Bu=Sonfau∖{u}B_u = Son_{fa_u} \setminus \{u\}。
还应注意，froot=0f_{\text{root}} = 0。
综上，有方程：
{fu=0u=rootfu=max⁡{ffauu≠rootn−szun−szu≤⌊n2⌋max⁡v∈Buszvunlimitedotherwise\begin{cases} f_u = 0&u = \text{root}\\ f_u = \displaystyle\max \begin{cases} f_{fa_u}&u \not= \text{root}\\ n - sz_u&n - sz_u \le \lfloor\frac{n}{2}\rfloor\\ \displaystyle\max_{v \isin B_u}sz_v&\text{unlimited} \end{cases}&\text{otherwise} \end{cases}
实际上，在实现过程中，有一个经典的 trick：
  • 维护最大次大，最小次小，快速解决树形 DP 合并时转移。
具体的，我们令 mx1,umx_{1,u} 表示以 uu 为父亲的点的子树大小的最大值，mx2,umx_{2,u} 为次大值，前面的转移将 BuB_u 等价为了 Sonfau∖{u}Son_{fa_u} \setminus \{u\}，这里减去的 {u}\{u\}，求可以用这个方法判断，如果最大值重了，就用最小值，否则最大值最优。
时间复杂度 O(n)O(n)。
codeCPP
#include<bits/stdc++.h>
#define endl '\n'
//#define MSOD


using namespace std;
using ll = long long;

constexpr ll N = 4e5 + 5;

ll n, ctd, mxx = LLONG_MAX;
ll dp[N], siz[N], mx1[N], mx2[N];
vector<ll> g[N];
inline void dfs_ctd(ll u, ll dad) {
	siz[u] = 1;
	ll mx = 0;
	for(auto v : g[u]) {
		if(v == dad) {
			continue;
		}
		dfs_ctd(v, u);
		siz[u] += siz[v];
		mx = max(mx, siz[v]);
	}
	mx = max(mx, n - siz[u]);
	if(mxx > mx) {
		mxx = mx, ctd = u;
	}
	return;
}
inline void dfs(ll u, ll dad) {
	siz[u] = 1;
	for(auto v : g[u]) {
		if(v == dad) {
			continue;
		}
		dfs(v, u);
		siz[u] += siz[v];
		if(siz[v] > mx1[u]) {
			mx2[u] = mx1[u], mx1[u] = siz[v];
		} else if(siz[v] > mx2[u]) {
			mx2[u] = siz[v];
		}
	}
	return;
}
inline void dfs1(ll u, ll dad) {
	dp[u] = dp[dad];
	if(mx1[dad] == siz[u]) {
		dp[u] = max(mx2[dad], dp[u]);
	} else {
		dp[u] = max(mx1[dad], dp[u]);
	}
	if(n - siz[u] <= n / 2) {
		dp[u] = max(dp[u], n - siz[u]);
	}
	if(u == ctd) {
		dp[u] = 0;
	}
	for(auto v : g[u]) {
		if(v == dad) {
			continue;
		}
		dfs1(v, u);
	}
	return;
}
inline void solve() {
	cin>>n;
	for(int i = 1 ; i < n ; i ++) {
		ll u, v;
		cin>>u>>v;
		g[u].push_back(v);
		g[v].push_back(u);
	}
	dfs_ctd(1, 0);
	dfs(ctd, 0);
	dfs1(ctd, 0);
	for(int i = 1 ; i <= n ; i ++) {
		cout<<((siz[i] >= n / 2 || n - siz[i] - dp[i] <= n / 2) ? 1 : 0)<<" ";
	}
	return;
}

signed main() {
	ios::sync_with_stdio(false), cout.tie(0), cin.tie(0);
	int TC = 1;
#ifdef MSOD
	cin>>TC;
#endif
	while(TC --) {
		solve();
	}
	return 0;
}

评论

共 0 条评论，欢迎与作者交流。

正在加载评论...